【经典算法学习-排序篇】直接选择排序

一、选择排序

1.基本概念和介绍

选择排序的核心思想是：每一趟从无序区中选出关键字最小（或最大）的元素，按顺序放在有序区的最后（生成新的有序区，无序区元素个数减1），直到全部排完为止。

换句话说就是：每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在待排序的数列的最前，直到全部待排序的数据元素全部排完。

• 直接选择排序

最基本的选择排序，又称简单选择排序，整个过程就是将无序区中的所有元素逐一比较，找到最小的元素，与无序区中的首个元素进行交换，有序区长度加1，无序区长度减1。重复以上的步骤，知道所有的元素都已经排完为止。

• 树形选择排序

又称锦标赛排序，是为了优化每次在排序中确定最小元素时比较次数过多的问题。借助树这种数据结构，对整个序列两两比较，将数值较小的元素上升到父节点，成为优胜者。最后的树记录着每一个优胜者之间的关系，按规则取出即可。

• 堆排序

对排序是一种对树形选择排序（锦标赛排序）的优化。由于树形选择排序需要花费较多的空间，造成空间复杂度提高，堆排序便构建一个小顶堆（在升排序列中），重复这个过程，直到排好所有的元素为止。

2.直接选择排序

例题1：

输入n个数，将这n个数按照从小到大排序。

• 输入

输入一个数字n和一个长度为n的序列，通常将这n个数直接放进数组中。

• 输出

输出一个新序列，满足按照从小到大的顺序排序（这里按照例题讨论升序排列，感兴趣可以自行讨论一下降序排列）。

• 算法说明

直接选择排序的排序流程大致如下：

第一趟，从n个数字中找到关键字最小的记录和第1个数交换；

第二趟，从(n-1)个数字中找到关键字最小的记录和第2个数交换；

第三趟，从(n-2)个数字中找到关键字最小的记录和第3个数交换；

∴总结归纳，可以理解为：

第 i 趟，从(n-i+1)个数字中找到关键字最小的记录和第i个数交换。

直到完成i=n-1时，整个循环有序排列。

• 算法流程

初始关键字 [53 76 34 52 98 35 65 79]

第一趟排序后 [34][53 76 52 98 35 65 79]

第二趟排序后 [34 35][53 76 52 98 65 79]

第三趟排序后 [34 35 52][53 76 98 65 79]

第三趟排序后 [34 35 52 53][76 98 65 79]

第四趟排序后 [34 35 52 53 65][76 98 79]

第五趟排序后 [34 35 52 53 65 76][98 79]

第六趟排序后 [34 35 52 53 65 76 79][98]

第七趟排序后 [34 35 52 53 65 76 79 98][]

最终结果 [34 35 52 53 65 76 79 98]

3.代码实现

#include 
 
using namespace std;
 
int main()
{
    int n, a[1024];
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    for (int i = 0; i < n - 1; i++)
    {
        //变量k用来记录无序区中最小的元素
        int k = i;
        //内层循环的作用是在无序区中选择最小的元素
        for (int j = i + 1; j < n; j++)
        {
            if (a[j] < a[k])
                k = j;
        }
        //如果本轮选出的元素没有在应该在的位置上就交换
        swap(a[i], a[k]);
    }
    for (int i = 0; i < n; i++)
        cout << a[i] << " ";
    return 0;
}

4.时间复杂度分析

• 最优情况

最优情况下，即一开始就是一个有序序列。但是即使是这样也还是要完成比较的过程，所以必定会执行两层循环，即时间复杂度为。

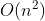• 最差情况 

在最差情况之下，循环也同样是被完全执行完成，但是也是执行了两层循环就结束了。所以，此时的时间复杂度和最优情况下相同，也是。

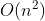• 平均情况

综合最优情况和最差情况，得到该算法的时间复杂度为：

这样的时间复杂度在所有的排序算法中算是非常高的了。

5.优劣分析

• 优点

循环的运行次数永远不会发生改变，永远为已知的(n-1)次。

• 缺点

总体来看，选择排序的比较次数多，并且时间复杂度高。另外一点，选择排序是一种不稳定的排序方式。

正是因为这样，选择排序才会衍生出很多优化的算法和代码。

二、总结

选择排序作为“百害无一利”的算法，秉承了时间复杂度高、比较次数多、不稳定等多重优势，让其他的算法也是“望山跑死马”了。

所以，我们后文也会介绍更多的更优算法，来帮助大家更好的学习算法。

三、课后小练习

没有课后小练习怎么行？！

奉上今日的课后题单，各位大佬们一定要接受这份提题单！

求知若渴，虚心若愚。

1176：谁考了第k名

车厢重组 - 洛谷

四、下期预告

木桶效应你听过没有？那我今天就带你见识见识！

我是Wanghs0716，一个来自北京景山学校的七年级小盆友，我们下期不见不散！

---

 The end