最小公倍数（三种解法）

  题目：给定两个正整数A和正整数B，编写代码求这两个数的最小公倍数，要求输入A和B（范围：1<=A,B<=100000）。

  首先，我们应该知道什么是最小公倍数：能够被几个数整除的那个数，就是这几个数的最小公倍数。知道了原理，下面就该思考如何实现代码了。

---

方法一：
  我们知道，A和B的最小公倍数最小的情况也不会比A和B中较大的那个数要小。所以只需现找出A和B中较大数作为最小公倍数的起始值，然后一直向后试除直到某个数能够同时整除A和B为止。那么此时该数就是A和B的最小公倍数。

//方法一（暴力求解法）：

#include

int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	//求出其中较大的值
	int m = (a > b ? a : b);
	//直到能被A和B整除的时候停下来，否则加加往后
	while ((m % a != 0) || (m % b != 0))
	{
		m++;
	}
	printf("%d\n", m);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

  该方法求解的效率比较低，因为我们是一个一个数去试除的，而且每次只是加1。不建议采纳此种想法。

---

方法二：
  我们发现A和B与其的最小公倍数M之间存在一个关系：A*i = B*j = M，只要当i从1开始向后尝试，直到A*i的值能够被B整除为止，此时的A*i的值就是A和B的最小公倍数。

//方法二（系数试除法）

#include

int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	int i = 1;
	while (1)
	{
		if ((a * i) % b == 0)
		{
			break;
		}
		i++;
	}
	printf("%d\n", a * i);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

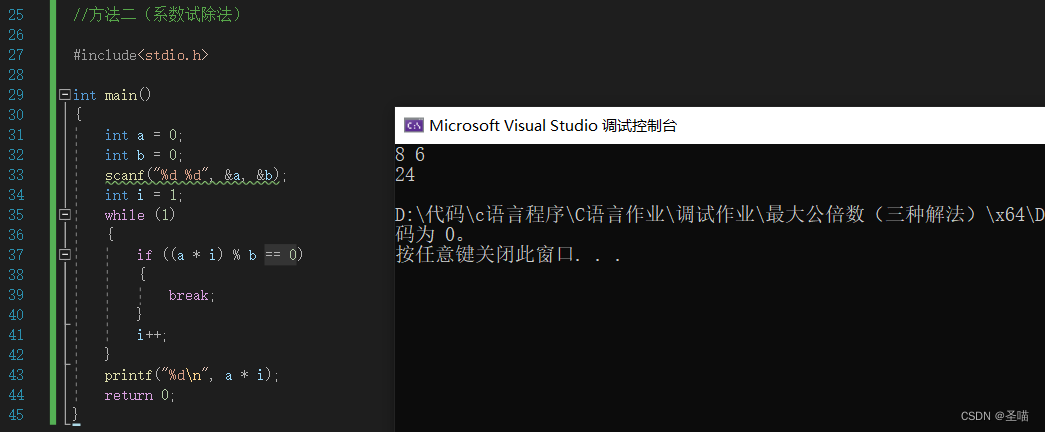
  该方法是通过试除系数来判断结果是否是最小公倍数，相较于之前的方法效率高了点，但如果遇见A的值远小于和B时，此时的效率就没那么高了。

---

方法三：
  我们可以通过A和B的最大公约数来求它们的最小公倍数，公式：A*B/最大公约数 = 最小公倍数。那最大公约数该怎么求呢？不知道大家有没有听说过 “辗转相除法”（就是现给定你两个数，将其中较大的数除以较小的数。若余数不为0，则将除数变为被除数，余数变为除数，继续进行上面的除法计算 ，直至余数为0。而此时的除数就是这两个数的最大公约数）。

//方法三（最大公约数求法）

#include

int main()
{
	int a = 0;
	int b = 0;
	int m = 0;//最大公约数
	scanf("%d %d", &a, &b);
	//创建被除数、除数、余数
	int x, y, z = 0;
	x = a;
	y = b;
	//求最大公约数
	while (y != 0)
	{
		z = x % y;
		x = y;
		y = z;
	}
	m = x;
	printf("%d\n", a * b / m);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

  该方法相较于之前两种方法，比较高效且稳定的多。

---

这份博客👍如果对你有帮助，给博主一个免费的点赞以示鼓励欢迎各位🔎点赞👍评论收藏⭐️，谢谢！！！
如果有什么疑问或不同的见解，欢迎评论区留言欧👀。