Regression（回归）的应用

 - 股票市场的预测
 - 无人驾驶汽车（方向盘的角度）
 - 用于给不同的顾客推荐不同的商品

应用举例——宝可梦的CP

step1:建立模型

设置Model为(其中，y为升级后的宝可梦的CP值，为升级前的宝可梦的CP值)，然后得到对应的一系列参数模型

举个例子:

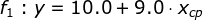
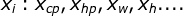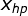我们可以看出，这个模型是线性模型，仅仅考虑了宝可梦进化前的cp值，但是进化后的cp值可能与其他条件有关，如宝可梦的身高、体重等等，所以将公式扩展为：，其中表示宝可梦进化后的cp值，各种特征，例如表示宝可梦进化前的cp值，表示宝可梦的生命值，表示体重，表示身高，，。

step2:函数的优度

训练数据：

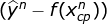判定函数优度的标准为损失函数： ，其中为基于输入函数估计的y，为预测误差。

即：

可视化效果：

 不同的b和w会产生不同的损失值，图中颜色代表损失值，红色代表损失值很大，紫色代表损失值最小。

step3 最佳函数

使得损失函数最小来确定最佳函数。

可用的方法是梯度下降法。

Gradient Descent——梯度下降法

分为两种情况——只有一个参数的情况、含有多个参数的情况。

一个参数

(1) 随机选一个初始值

(2) 计算loss函数对的微分，即，亦为这一点处loss曲线的斜率。

(3) 若这点切线斜率为负值（Negative）,说明曲线左高右低，这个时候需要增加，从而使得损失函数变小；若这点切线斜率为正值（Positive）,说明曲线左低右高，这个时候需要减小，从而使得损失函数变小。

那么改变量究竟为多少？

首先取决于斜率的大小，若斜率比较大，则改变量偏小； 若斜率比较小，则改变量偏大。

其次取决于常数项，也称学习率（learning rate），若学习率较大， 则改变量偏大； 若斜率比较小，则改变量偏小。

 所以每次改变量为，即：

以此类推，直到，此时，找到局部最小值。

两个参数

（1）随机选择两个参数，分别为。

（2）loss函数分别对两个参数进行偏微分。

（3）改变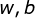的值。如下：

，

，

以此类推，直到&&时，

可视化效果：

 越偏蓝色表示损失值越小，越偏红色表示损失值越大。

 梯度下降的缺点

最后得到的最小值点是局部最小值点

有关宝可梦的实际操作

（1）假设有十只宝可梦，模型选择为。先建立损失函数，分别对两个参数进行偏微分。

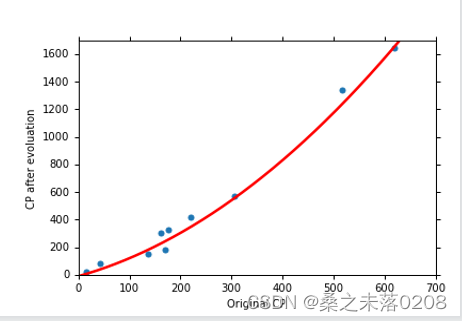
 （2）通过图中原始cp和进化后的cp对比，可以得到当前参数，与此同时，平均误差为31.9，测试数据的平均误差为35，偏大。

（3）所以选择其他模型，得到参数为，训练数据的平均误差为15.4，测试数据的平均误差为18.4，相较于第一次模型较好。

（4）那么，考虑一下是否能构建更好的模型？

先构建模型：，得到参数为，训练数据的平均误差为15.3，测试数据的平均误差为18.1，相较于第二次模型更好一些。

再考虑，训练数据的平均误差为14.9，测试数据的平均误差为28.8，结果变差。

 最后考虑，训练数据的平均误差为12.8，测试数据的平均误差为232.1。结果变得非常差！

 

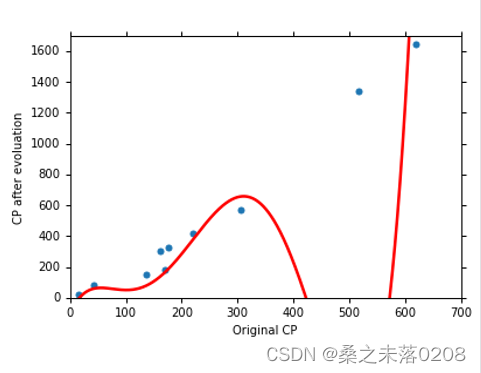
（5）五种模型的对比

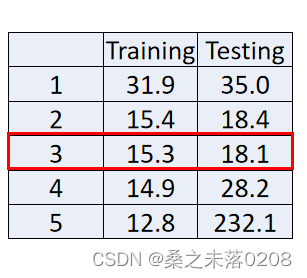
 我们可以看出当模型越来越复杂时，训练数据的平均误差会越来越小，但是测试数据的平均误差会越来越大，尤其到后面出现大幅度增长（如下图所示），我们称这种现象为过拟合。 

（6）解决过拟合的方法

我们可以推测不同的宝可梦进化前后的cp值存在差异，所以不能一概而论。这就是我们之前未考虑的隐藏因素。 

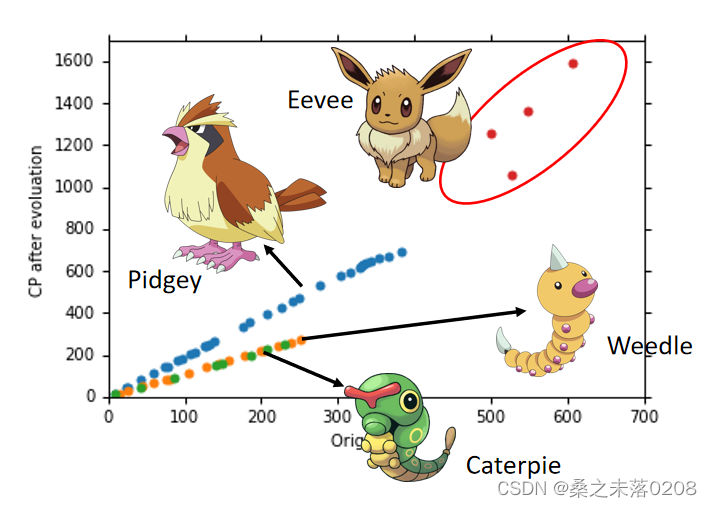
 所以返回到第一步构建模型时，对于不同种类的宝可梦，建立不同的模型（即参数不同），如下图所示：

那么，如何将这个模型变成线性模型？借助一个，。

 

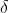计算出来训练误差是1.9，测试误差是102.3，依旧过拟合。 解决此问题有一办法——正则化（regularization）。即在损失函数后加入一项，更小的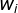意味着函数更加顺滑，而其中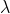其实是需要手调的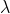，​​​​​​​的大小取决于你希望你的函数有多平滑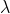，​​​​​​​越大函数就越平滑。

从上图可以看出，当 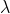从小增大到一定的值，训练误差越来越大，反而测试误差越来越小。但是从该值再开始增大，训练误差越来越小，反而测试误差越来越大。

我们喜欢平滑程度刚刚好的函数，因为它对噪声不那么敏感，而且也不会失去对数据的拟合能力，因此我们选择λ=100。