参考：蘑菇书EasyRL 

目录

1.梯度策略算法

2.梯度策略技巧

2.1 添加基线(baseline)

2.2 分配合适的分数(credit)

2.3 评论员(critic)

3.REINFORCE：蒙特卡洛策略梯度

---

1.梯度策略算法

强化学习有 3 个组成部分：演员（actor）、环境和奖励函数。环境和奖励是学习前就给定的，因此我们能做的就是调整演员的策略，使其得到最大的奖励。

 策略记作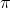，例如在深度强化学习中，策略就是一个网络，网络中有一些参数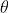，将状态（向量或矩阵）输入到网络中，会输出动作的概率分布。策略也可以理解为某一状态下演员给出各个动作的概率分布。

演员和环境交互过程如下：环境给出一个状态，演员看到这个状态会给出一个动作，环境根据发生一些变化，产生新的状态，如此不停的持续这个过程直到环境停止。

 在一次交互过程中，将环境输出的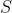和演员输出的组合起来就是一个轨迹Trajectory

 给定演员参数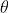就可以计算某个轨迹发生的概率

 先计算环境输出的概率，再计算演员根据执行的概率，环境根据生成，环境根据演员的动作生成新状态是否存在概率分布取决于内部设定，一般来说存在概率，如此便能计算出某个轨迹发生的概率。上式中代表环境，预先设定，代表演员，取决于参数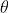，是我们可以优化和控制的。

除了环境和演员，奖励是非常重要的部分。演员每次根据环境输出的状态给定一个动作就会得到一个奖励，将一个轨迹的所有奖励加起来得到。因为演员在某状态下采取什么样的动作是有随机性的，环境给出的观察也是有随机性，因此是一个随机变量，我们只能得到期望奖励，训练目标是最大化期望奖励，使用梯度上升（gradient ascent）。

进行梯度上升首先要计算期望奖励的梯度，经过一系列数学公式计算可以得到如下：

其中是轨迹的奖励，是某一状态下采取某一动作的对数概率。通过梯度上升来更新参数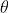，如果在执行最后结束发现是正的，就增加执行概率，反之则减少这个概率。

2.梯度策略技巧

2.1 添加基线(baseline)

如果给定状态 s 采取动作 a，整场游戏得到正的奖励，就要增加(s, a) 的概率。如果给定状态 s 执行动作 a，整场游戏得到负的奖励，就要减小 (s, a) 的概率。但在很多游戏里面，奖励总是正的，最低都是 0。假设某一个状态有三个动作a,b,c，由于奖励为正，梯度更新时会将三个动作的对数概率都提高，但是权重不一样，权重小的，该动作的概率提高的就少；权重大的，该动作的概率提高的就多。动作a,b,c的对数概率和为0，所以提高少的，在做完归一化（normalize）以后，动作 b 的概率就是下降的；提高多的，该动作的概率才会上升。

 这只是理想状况，实际上我们是通过采样得到的期望，有一些动作可能没有被采样到，假设a没有被采样到 ，b和c的对数概率要变大，相应a的对数概率就要变小，但是a不一定是一个不好的动作，仅仅是因为它没有被采样到。

为了解决这个问题，就要将奖励设置不总是正的，将奖励减去b

b称为基线，这样有正有负，如果得到的总奖励，就让 (s, a) 的概率上升。如果，就算 是正的，值很小也是不好的，我们就让 (s, a) 的概率下降，让这个状态采取这个动作的分数下降。b可以取 的均值，因此训练过程中会不断记录

2.2 分配合适的分数(credit)

在梯度上升公式中，一个ep里面的所有(s,a)是相同的权重，这显然是不合理的。例如在同一场游戏里面，也许有些动作是好的，有些动作是不好的。假设整场游戏的结果是好的，但并不代表这场游戏里面每一个动作都是好的。若是整场游戏结果不好，但并不代表游戏里面的每一个动作都是不好的。所以我们希望可以给每一个不同的动作前面都乘上不同的权重。每一个动作的不同权重反映了每一个动作到底是好的还是不好的。

在第一场游戏中，权重是3，但是3不是执行的结果，相反因为执行了，进入再执行动作得到了-2。在第二场游戏中，权重是-7，-7也不是执行的结果，而是执行。因此整场游戏的结果好坏并不能代表动作的好坏。

一个做法是计算某个状态-动作对的奖励的时候，不把整场游戏得到的奖励全部加起来，只计算从这个动作执行以后得到的奖励。因为这场游戏在执行这个动作之前发生的事情是与执行这个动作是没有关系的，所以在执行这个动作之前得到的奖励都不能算是这个动作的贡献。我们把执行这个动作以后发生的所有奖励加起来，才是这个动作真正的贡献。上图中的权重就变成了-2。

更近一步，将未来的奖励考虑折扣因子，动作对未来奖励的影响是随着步长增加而减少的。例如上图中第一场游戏权重就变成了 。

2.3 评论员(critic)

前文中的b是一个网络估计出来的，是一个网络的输出，R-b称为优势函数，用表示。计算优势函数值，需要先有一个模型与环境交互，才能知道接下来的奖励。优势函数的意义是，假设我们在某一个状态执行某一个动作，相较于其他可能的动作，有多好。优势函数在意的不是绝对的好，而是相对的好，即相对优势（relative advantage）。因为在优势函数中，我们会减去一个基线 b，所以这个动作是相对的好，不是绝对的好。 通常可以由一个网络估计出来，这个网络称为评论员（critic）

3.REINFORCE：蒙特卡洛策略梯度

蒙特卡洛方法可以理解为算法完成一个回合之后，再利用这个回合的数据去学习，做一次更新。因为我们已经获得了整个回合的数据，所以也能够获得每一个步骤的奖励，我们可以很方便地计算每个步骤的未来总奖励，即回报 。是未来总奖励，代表从这个步骤开始，我们能获得的奖励之和。相比蒙特卡洛方法一个回合更新一次，时序差分方法是每个步骤更新一次，即每走一步，更新一次，时序差分方法的更新频率更高，因为不知道未来的奖励，所以使用Q值近似G

REINFORCE是策略梯度中最简单也是最经典的一个算法，在代码处理上先获取每个步骤的奖励，再计算未来的总奖励，代入下列公式从而优化每个动作的输出，也就是说 比较容易计算

REINFORCE比较关键的是伪代码后4行， 先产生一个回合的数据（s,a,G)，再针对每个动作计算梯度

网络预测每个状态下应该要输出的动作概率分布，比如 0.2、0.5、0.3，实际上输出给环境的是随机选择一个动作，例如如果选择向右，那么独热向量就是（0,0,1）。我们把神经网络的输出和实际动作代入交叉熵的公式就可以求出输出动作的概率和实际动作的概率之间的差距。但实际的动作只是我们输出的真实的动作，它不一定是正确的动作，它不能像手写数字识别一样作为一个正确的标签来指导神经网络朝着正确的方向更新，所以我们需要乘一个奖励回报。相当于对真实动作的评价。如果 越大，未来总奖励越大，那就说明当前输出的真实的动作就越好，损失就越需要重视；如果​​​​​​​ 越小，未来总奖励越小，那就说明当前输出的真实的动作就越不好，权重就小一点，优化力度也要小一点。

下图为REINFORCE 算法示意，首先我们需要一个策略模型来输出动作概率，输出动作概率后，通过 sample() 函数得到一个具体的动作，与环境交互后，我们可以得到整个回合的数据。得到回合数据之后，我们再去执行 learn() 函数，在 learn() 函数里面，我们就可以用这些数据去构造损失函数，“扔”给优化器优化，更新我们的策略模型。

 在pytorch官网中给出了相应的方法和代码Probability distributions - torch.distributions — PyTorch 1.12 documentation

from torch.distributions import Categorical
 
probs = policy_network(state)
m = Categorical(probs)
action = m.sample()
next_state, reward = env.step(action)
# 乘负号是因为优化器默认梯度下降，而此处需要梯度上升
loss = -m.log_prob(action) * reward
loss.backward()

• Categorical类：创建一个分类分布即离散概率分布
• sample()：Categorical类的一个方法，用于采样
• log_prob()：Categorical类的一个方法，返回对数概率

from torch.distributions import Categorical
import torch
probs = torch.tensor([0,2, 0.3, 0.5])
 
# 创建分类分布
m = Categorical(probs)
m
Out[6]: Categorical(probs: torch.Size([4]))
 
# 随机采样一个动作作为真实动作
action = m.sample()
action
Out[15]: tensor(1)
 
# 增加动作的概率
m.log_prob(action)
Out[16]: tensor(-0.3365)