蒙特卡洛策略梯度（REINFORCE算法）及其改进

蒙特卡洛策略梯度（REINFORCE算法）

回顾

策略梯度中的梯度等于：某一状态下采取某一动作的对数概率乘以一个权重。而这个权重就是回合中的奖励值。

蒙特卡洛策略梯度：REINFORCE

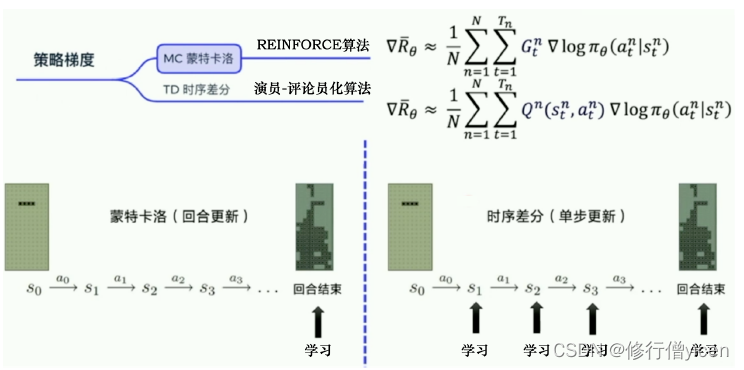
蒙特卡洛算法的核心就是智能体与环境必须完成一个完整的Episode交互。当智能体完成一个Episode后，再利用获得的数据（或轨迹）进行智能体参数$\theta$的更新。即一个Episode，参数更新一次。

根据轨迹数据，可以计算出每一步骤之后未来总奖励$G_t$。$G_1$表示从第一步往后所能得到的未来总奖励；$G_2$表示从第二步往后所能得到的未来总奖励；依次类推。

计算每一步未来总奖励$G_t$

在训练中可以用列表来依次存储state,action 和reward，具体代码可以表示为：

class Agent():
    def __init__(self, state_dim, action_dim):
    	....其他参数
        self.episode_s = []
        self.episode_a = []
        self.episode_r  = []
    def store(self, state, action, reward): # 保留回合中的数据
        self.episode_s.append(state)
        self.episode_a.append(action)
        self.episode_r.append(reward)
    def learn(self):
    	# 计算从每一个时刻开始，到回合结束所得到的折扣奖励
        G = []
        g = 0
        for r in self.episode_r[::-1]:
            g = self.gamma * g + r
            G.insert(0,g)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

计算动作概率

class Policy(nn.Module):
    def __init__(self, s_dim, a_dim, h_dim):
        super(Policy, self).__init__()
        self.s_dim = s_dim
        self.a_dim = a_dim
        self.h_dim = h_dim
        self.fc1 = nn.Linear(self.s_dim, self.h_dim)
        self.fc2 = nn.Linear(self.h_dim, self.a_dim)
    def forward(self, state):
        s = F.relu(self.fc1(state))
        a_prob = F.softmax(self.fc2(s),dim=1)
        return a_prob
1
2
3
4
5
6
7
8
9
10
11
12

交互过程中，选择动作

def choose_action(self, state,deterministic):
    state = torch.tensor(state,dtype=torch.float).to(device)
    state = torch.unsqueeze(state,dim=0)  
    a_prob = self.policy(state).cpu().data.numpy().flatten()
    if deterministic:
        a = np.argmax(a_prob)
    else:
        a = np.random.choice(range(self.a_dim),p=a_prob)
    return a
1
2
3
4
5
6
7
8
9

策略更新

策略的loss就是每一步未来总奖励乘以相应动作的对数概率。

def learn(self):
    	# 计算从每一个时刻开始，到回合结束所得到的折扣奖励
        G = []
        g = 0
        for r in self.episode_r[::-1]:
            g = self.gamma * g + r
            G.insert(0,g)
            
        for i,s in enumerate(self.episode_s):
            state = torch.unsqueeze(torch.tensor(s,dtype=torch.float),dim=0).to(device)
            a = self.episode_a[i]
            a_prob = self.policy(state).flatten() # 展开
            g = G[i]
            #loss = - g * torch.log(a_prob[a]) # loss1
            loss = - pow(self.gamma, i) * g * torch.log(a_prob[a])# loss2
            # 测试结果显示，loss的收敛效果会更好。第一种方差很大。
            self.policy_optim.zero_grad()
            loss.backward()
            self.policy_optim.step()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

蒙特卡洛策略梯度：REINFORCE,使用baseline

当使用baseline策略时，我们需要使用网络计算b。故多增加一个网络

class Value(nn.Module):
    def __init__(self, state_dim, hidden_width):
        super(Value, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_width)
        self.fc2 = nn.Linear(hidden_width, 1)

    def forward(self, s):
        s = F.relu(self.fc1(s))
        v_s = self.fc2(s)
        return v_s
1
2
3
4
5
6
7
8
9
10

策略更新

def learn(self):
    G = []
    g = 0
    for r in self.episode_r[::-1]:
        g = self.gamma * g + r
        G.insert(0,g) # 在列表的index=0的位置插入元素g

    for i,s in enumerate(self.episode_s):
        state = torch.unsqueeze(torch.tensor(s,dtype=torch.float),dim=0).to(device)
        a = self.episode_a[i]
        a_prob = self.policy(state).flatten() # 展开
        g = G[i]
        v_s = self.value(state).flatten()
        # policy_loss = - pow(self.gamma, i) * (g-v_s.detach()) * torch.log(a_prob[a])
        policy_loss = - (g - v_s.detach()) * torch.log(a_prob[a])

        self.policy_optim.zero_grad()
        policy_loss.backward()
        self.policy_optim.step()

        value_loss = (g-v_s)**2
        self.value_optim.zero_grad()
        value_loss.backward()
        self.value_optim.step()
    self.episode_s, self.episode_a, self.episode_r = [],[],[] # 一个回合的数据只能用一次
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

注意

蒙特卡洛策略梯度算法，每一个回合的数据只能用一次。用完就扔掉。

使用时序差分方法

• 蒙特卡洛方法的智能体每次都要走完一个Episode后，参数才能开始更新，更新频率比较慢。
• 而时序差分方法的更新频率更高。该方法是使用$Q(s,a)$来近似代替REINFORCE算法中的$G_t$。

参考

https://github.com/Lizhi-sjtu/DRL-code-pytorch/tree/main/1.REINFORCE