1. 冒泡排序

• 什么是冒泡排序？

​冒泡排序是一种简单的排序算法。顾名思义，即跟水中的气泡一样，轻的（较小的元素）会率先上浮到水面，所有元素”气泡“轻重不一，那么上浮的过程就已经逐渐排序好。对应到算法里，假设要从小到大排序，那么从数列从左向右第一个元素起，每次比较两个元素，①左边大于右边就交换，然后该元素继续和下一个元素比较；②左边小于右边就不变，然后对象换为右边这个，继续和下一个比较。

直至第一次比较再没有交换的情况，第一次循环就结束了。然后再次开始下一次循环。最终所有元素从左到右都没有再交换的情况时，待排序数列就已经变为有序。 看一下算法描述。

1.1 算法描述

① 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
② 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样③ 在最后的元素应该会是最大的数；
④ 针对所有的元素重复以上的步骤，除了最后一个；
⑤ 重复步骤1~3，直到排序完成。

1.2 时空复杂度

• 时间复杂度：O(n²) ，最好O(n)， 最坏O(n²)
• 空间复杂度：O(1)
• 算法稳定性：稳定（a=b排序后相对位置仍然不变）

1.3 动图演示

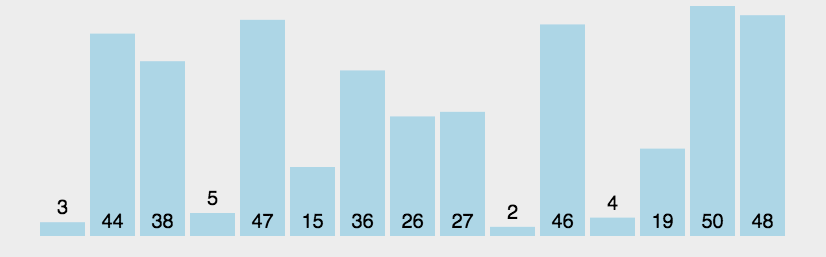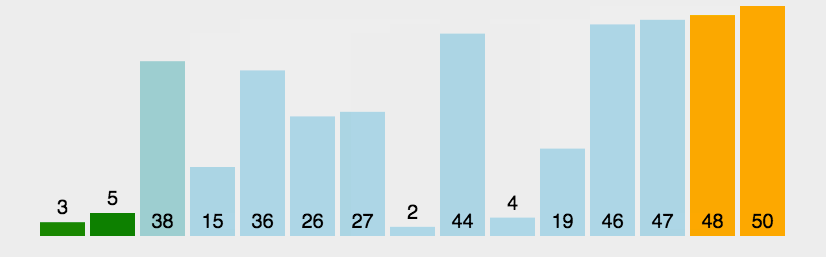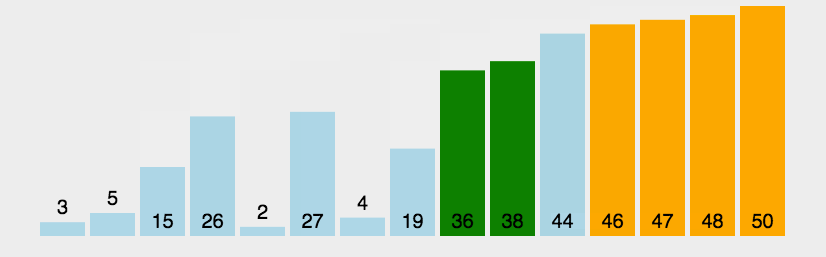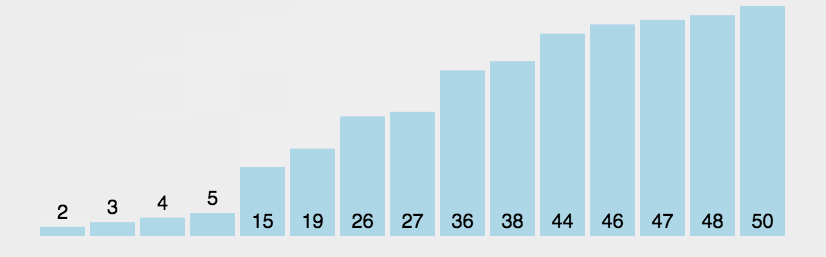
1.4 算法实现

function bubbleSort(arr) {
    int len = arr.length;
    for (int i = 0; i < len - 1; i++) {
        for (int j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j+1]) {        // 相邻元素两两对比
                var temp = arr[j+1];        // 元素交换
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

2. 冒泡排序优化版

我们知道，冒泡排序两个大循环，按上面的初始版本来说，需要把所有循环都走一遍才会结束。但是，有没有这样一种可能，我最外层的大循环只循环了，1次，2次就已经整个数列都有序了呢？但是算法不知道，还会傻乎乎地去继续执行剩下的遍历步骤，那这不是浪费人生嘛！所以我们有了改进一点的算法，一旦我判断到整个数列已经有序了，那我就不会有下次一定了，这次就投个币结束（doge）。

来看一下优化：

public static int[] bubbleSort(int[] arr) {
     if (arr == null || arr.length < 2) {
          return arr;
     }
    for (int i = 0; i < arr.length - 1; i++) {
         boolean isSorted  = true;//有序标记，每一轮的初始是true
         for (int j = 0; j < arr.length -i - 1; j++) {
             if (arr[j + 1] < arr[j]) {
                 isSorted  = false;//有元素交换，所以不是有序，标记变为false
                 int t = arr[j];
                 arr[j] = arr[j+1];
                 arr[j+1] = t;
             }
         }
         //一趟下来是否发生位置交换，如果没有交换直接跳出大循环
         if(isSorted )
              break;
     }
     return arr;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

特别好理解，假设我现在是第一次大循环，然后我默认标志为true。表示初始我们还没有发生元素交换。然后再执行内层循环，一旦内层循环发生交换了，那么我的标志变为false，表示”我发生交换啦~“，这是普通情况；然后看特殊情况，假设我这个数列本来就有序呢？那我第一次大循环进来后，标志为true，接着进入内层循环，比啊比，比完了都没有发生过一次交换，我的标志还是true。这说明了什么？说明我累死累活跑了一趟，结果没一个跟我交换，中间接力的也没发生交换，合着刚好后边的都比前面的大（或一样），那小循环结束后，我还要再继续走第二次、第三次大循环吗？这不多此一举么。所以赶紧结束！

3. 冒泡排序升级版

上面第2版解决了我数列一旦已经处于有序，后续就不必再执行剩下的步骤的问题。那么还有没有其他可以优化的地方呢？还真有。

• 结合动图来看，我们可以知道每趟排完序在数列末尾都会有最少一个元素占着坑位不再挪动屁股。那么我们就可以让新来的元素随着占坑位越来越多的元素不去试图跟他们抢位置。因为它们都已经明确位置了，是固定车位。
• 这样一来，我们是不是无形中又少了几次比较？哈哈，真开心~

• 实现原理

我们每一次排序都记录一下最后一次发生元素交换的位置，因为它就是无序区的边界。在它之后都是有序区的元素了。我们后面就不需要再进行比较了。

来看代码：

public static int[] bubbleSort(int[] arr) {
     if (arr == null || arr.length < 2) {
          return arr;
     }
    //记录最后一次交换的位置
    int lastExchangeIndex = 0;
    //无序数列的边界，每次比较只需要比到这里为止
    int sortBorder = arr.length - 1;
    
    for (int i = 0; i < arr.length - 1; i++) {
         boolean isSorted  = true;//有序标记，每一轮的初始是true
         for (int j = 0; j < sortBorder; j++) {
             if (arr[j + 1] < arr[j]) {
                 isSorted  = false;//有元素交换，所以不是有序，标记变为false
                 int t = arr[j];
                 arr[j] = arr[j+1];
                 arr[j+1] = t;
                 lastExchangeIndex = j;
             }
         }
        sortBorder = lastExchangeIndex
         //一趟下来是否发生位置交换，如果没有交换直接跳出大循环
         if(isSorted )
              break;
     }
     return arr;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

活动地址：CSDN21天学习挑战赛

---

无聊不是因为没事可做，而是因为对事不够投入。
​