目录

题目

前置知识复习

什么是完全二叉树？

什么是堆？

堆可以怎么分类？

堆相关操作中的时间复杂度

C++中堆的定义

题目解析

AC代码

---

题目

前置知识复习

什么是完全二叉树？

在深度为h的二叉树中，除了最后一层的结点数量可以不是满的之外，其余层的结点的数量都是满的。 

什么是堆？

堆是一种基于完全二叉树的数据结构。 

堆可以怎么分类？

可以分为大根堆和小根堆。

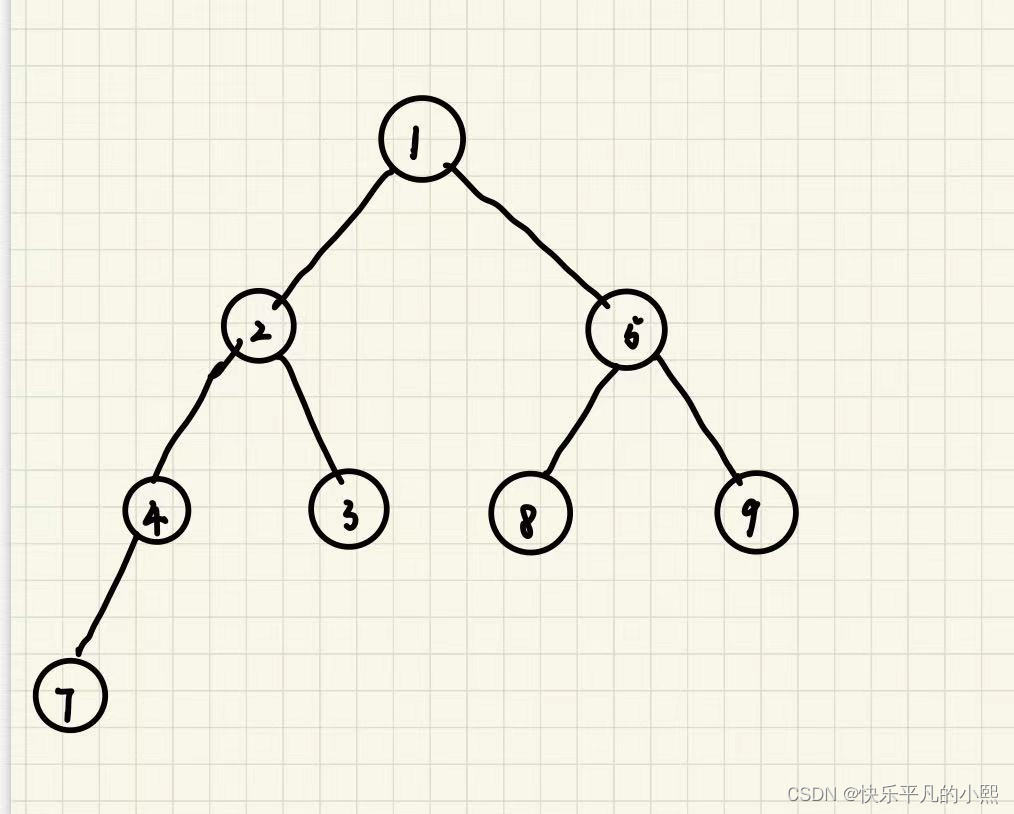
大根堆：在大根堆中每个节点的值都大于等于其子节点。如下图，

小根堆：在小根堆中每个节点的值都小于等于其子节点。 

堆相关操作中的时间复杂度

插入和删除：O(log N) 

由于堆的删除只可以删除堆顶的元素，而插入要维护堆本身的性质，所以都存在结点交换位置上移地情况。时间复杂度和实现堆的完全二叉树的高度息息相关。

堆排序：O(n*logn)

相当于进行n次插入的操作，时间复杂度就是O(n*logn)。

C++中堆的定义

priority_queue<int, vector<int>, less<int>>s;//less表示按照递减(从大到小)的顺序插入元素
priority_queue<int, vector<int>, greater<int>>s;//greater表示按照递增（从小到大）的顺序插入元素

题目解析

问题一：怎么求取这一串数字的中位数？

答：要求一串数字的中位数，我们需要的无非就是把这一串数字从小到大排列找出处于中间位置的数据。 

问题二：怎么实现？

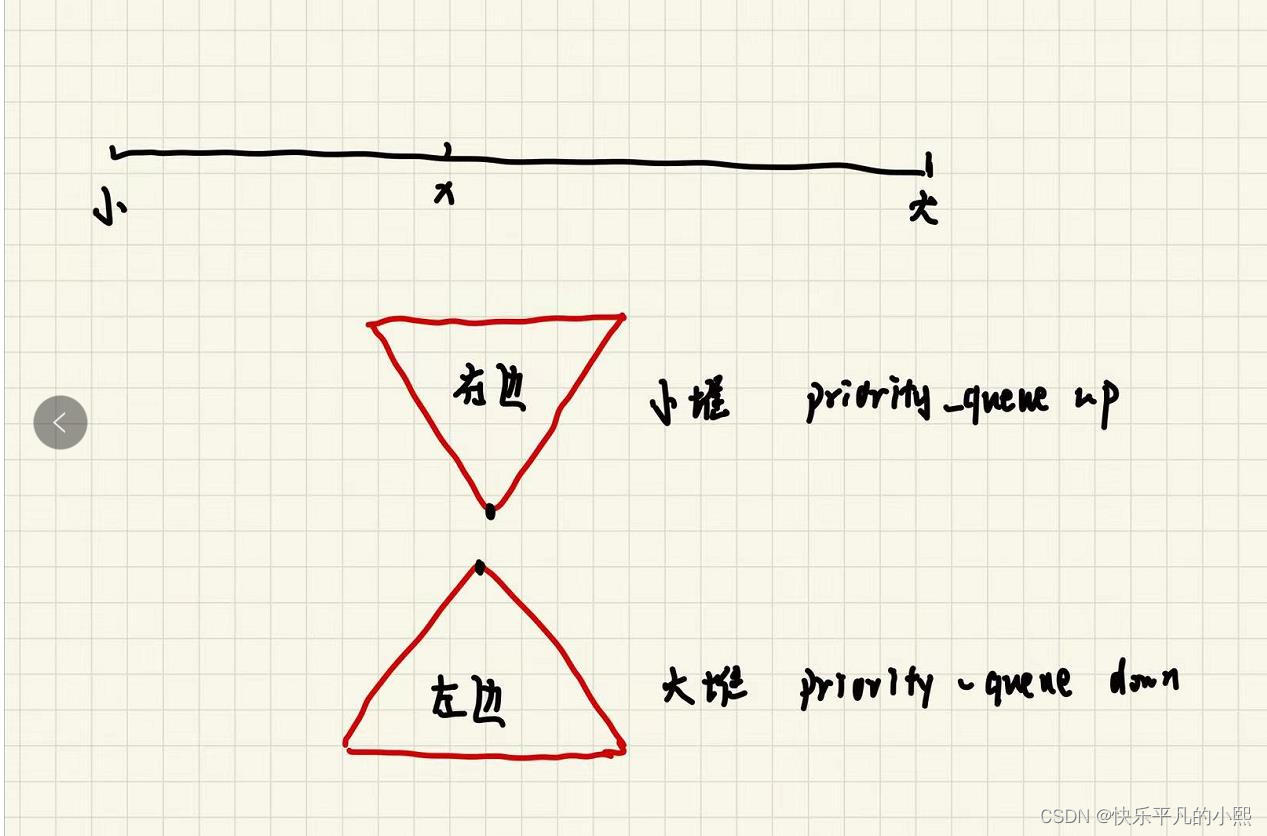
答： 用两个堆来实现，分别存储的是中间数字x左右两侧的数据。左侧的是要取较最大的那一个数字，左侧用大根堆来维护，右侧的目标是要取最小的那一个数字，用小根堆来维护。

问题三：怎么保障维护左右两侧的数据的堆中的数据的数量处于相等或者是左侧正好比右侧多一个的情况（怎么维护左右大小根堆的数据平衡）？

答：加两个特判，处理左侧数据的大根堆的时候假如打破了数据平衡就加特判将大根堆的元素弹出并且加到右侧的小根堆里面去；处理右侧数据的小根堆的时候假如打破了数据平衡就加特判将小根堆的元素弹出并且加到左侧的大根堆里面去。

AC代码

class Solution {
public:
    priority_queue<int, vector<int>, greater<int>> up;  //小根堆
    priority_queue<int> down;  // 大根堆
    //始终保障大小根堆相同或者大根堆比小根堆数量多一个的情况
    void Insert(int num) {
           if (down.empty() || num <= down.top()) {//特判一
            down.push(num);
            if (down.size() > up.size() + 1) {
                up.push(down.top());
                down.pop();
            }
        } else {
            up.push(num);
            if (up.size() > down.size()) {//特判二
                down.push(up.top());
                up.pop();
            }
        }
    }
 
    double GetMedian() { 
      if ((down.size() + up.size()) % 2) return down.top();
        return (down.top() + up.top()) / 2.0;
    }
 
};