2022_08_04_106期__栈和队列

目录

顺序表和链表的优缺点

顺序表的优点

顺序表的缺点：

链表的优点：

链表的缺点：

栈

实现栈。

栈的初始化

栈的销毁

栈的插入：

栈的删除

栈的访问：

栈的数量

打印栈

有效的括号

队列：

队列的初始化：

队列的销毁：

接下来，我们来实现队列的插入：

接下来，我们来讲删除队列元素

取队头和队尾的数据：

判断队列是否为空

查找链表的元素：

---

顺序表和链表的优缺点

 总结：

顺序表的优点

1：尾插尾删效率很高，扩容方便，一次就扩容两倍的容量。

2：随机访问：顺序表可以用下标访问元素。

顺序表的缺点：

1：头部和中部的插入和删除效率低，原因是需要挪动数据。---O(N)

2：扩容---性能消耗+空间浪费

链表的优点：

1：任意位置的插入和删除效率都很高 ---O(1)

2:按需申请释放

链表的缺点：

1：不支持随机访问

总结：顺序表能满足我们的基本要求，顺序表的效率更高。

但是注意也是有例外，假如我们大量进行头部的插入和删除，那我们还是用链表最好。

栈

 我们先分析后进先出：

例如：

 我们的元素是从栈顶进去的，我们依次向栈中输入数据1，2，3，4，5.

 接下来，假如我们要从栈中去除数据，那么我们就要首先取出后进去的5.这就是后进先出的含义。

我们把栈的插入操作叫做入栈，入数据在栈顶

我们把栈的删除操作叫做出栈，出数据也在栈顶，

注意：栈也是线性表，线性表一般就是用数组和链表实现的。

我们写一个题目：

 我们进行画图分析，首先看A选项，1，4，3，2.

这个是1先进，然后1出，然后2，3，4再进，然后2，3，4出，如图

依次演变的顺序为

 

 然后1出栈

 然后2，3，4再入栈

再出栈：

 我们再分析b选项：2，3，4，1

我们先入栈1，2

 然后我们出栈2

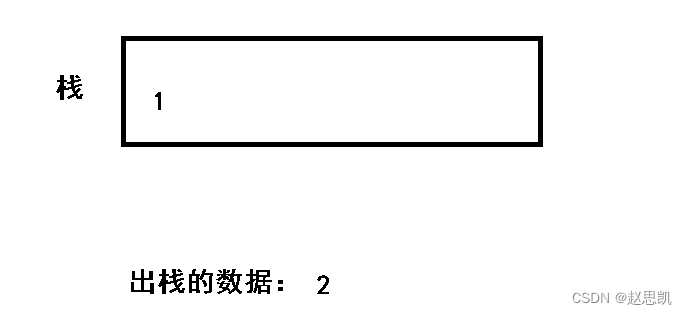
 然后我们入栈3

 然后我们出栈3：

 再入栈4

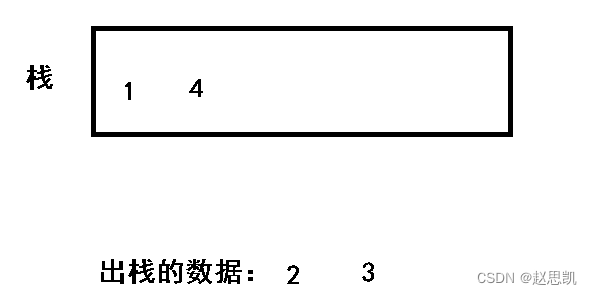
 再出栈1，4

 我们再来分析c选项：3 1 4 2

所以我们要入栈1 2 3

 然后我们出栈3

 但是我们发现：接下来是无法出栈1的，所以c选项错误。

实现栈。

我们可以用顺序表的方式实现栈

#pragma once
#include
//#define N 100 
typedef int STDataType;
struct Stack
{
	STDataType*a;
	int top;
	int capacity;
}ST;

 top表示我们的栈顶。

接下来， 我们来实现栈函数

void StackInit(ST*ps);
void StackDestory(ST*ps);
void StackPush(ST*ps, STDataType x);
void StackPop(ST*ps);
STDataType StackTop(ST*ps);
bool StackEmpty(ST*ps);
int StackSize(ST*ps);

由上到下分别是栈的初始化，栈的销毁，栈的插入，栈的删除，栈顶位置，判定栈是否为空，栈的大小。

栈的初始化

void StackInit(ST*ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

接下来，我们写

栈的销毁

void StackDestory(ST*ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

栈的插入：

void StackPush(ST*ps, STDataType x)
{
	assert(ps);
	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity = 0 ? 4 : ps->capacity * 2;
		STDataType*tmp = (STDataType*)realloc(ps->a, newCapacity*sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newCapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}

 top是我们的栈顶的位置，因为我们的栈是后进先出，所以对应的图像为：

 假如我们插入元素时

 

 最后的图像为

 而capacity是我们的顺序表的容量

 当我们的容量和我们的栈顶相等时，我们就需要扩容。

int newCapacity = ps->capacity = 0 ? 4 : ps->capacity * 2;

当栈中没有元素时，容量和栈顶相等，所以我们要先开辟一部分空间，这里的意思是假如容量为0，返回4，也就是初始容量为4，假如容量不为0，就扩容二倍。

STDataType*tmp = (STDataType*)realloc(ps->a, newCapacity*sizeof(STDataType));

上一句话只是计算出所要扩容元素的个数，而这里表示扩容元素，ps->a就表示我们数组首元素的地址，所以我们要在数组首元素的地址处扩容newCapacity*sizeof(STDataType个字节。然后赋给tmp。因为realloc有失败的风险，失败的话，就会导致ps->a为空指针，造成内存泄漏，所以我们先创建一个临时变量tmp来接受，假如tmp不为空指针，我们再把他赋给ps->a

if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}

 这里表示假如realloc扩容内存失败的时候，打印对应的错误信息并退出函数。

ps->a = tmp;
		ps->capacity = newCapacity;

每一次进入这个扩容函数都要使相应的ps->a和ps->capacity发生变化才是真正的扩容。

接下来，我们实现

栈的删除

void StackPop(ST*ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	--ps->top;
}

assert(!StackEmpty(ps));

这句话的意思是假如栈不为空时，进入函数。

栈的访问：

STDataType StackTop(ST*ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];
}

栈的数量

int StackSize(ST*ps)
{
	assert(ps);
	return ps->top;
}

打印栈

int main()
{
	ST st;
	while (!StackEmpty(&st));
	{
		printf("%d ", StackTop(&st));
		StackPop(&st);
	}
	printf("\n");
	return 0;
}

while (!StackEmpty(&st))

判断栈是否为空，不为空时，打印栈位置对应的元素，然后出栈，继续循环。

力扣

有效的括号

bool isValid(char* s)
{
	ST st;
	StackInit(&st);
	while (*s)
	{
		if (*s == '{' || *s == '}' || *s == '(')
		{
			StackPush(&st, *s);
		}
		else
		{
			if (StackEmpty(&st))
				return false;
			char top = StackTop(&st);
			StackPop(&st);
			if ((*s == '}'&&top != '{')
				|| (*s == ']'&&top != '[')
				|| (*s == ')'&&top != '('))
			{
				return false;
			}
		}
		++s;
	}
	StackDestory(&st);
}

队列：

 队列需要用链表来实现。

#pragma once
#include
#include
#include
#include
typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode*next;
	QDataType data;
}QNode;

我们把链表重命名为QNode

因为我们的队列是先进先出，也就是说我们入列是在队尾，出列是在队头，所以我们需要两个指针，分别指向链表的头和链表的尾。

typedef struct Queue
{
	QNode*head;
	QNode*tail;
}Queue;

创建一个结构体，结构体有两个指针，分别指向链表的头和链表的尾

void QueueInit(Queue*pq);
void QueueDestory(Queue*pq);
void QueuePush(Queue*pq,QDataType x);
void QueuePop(Queue*pq);
QDataType QueueFront(Queue*pq);
QDataType QueueBack(Queue*pq);
bool QueueEmpty(Queue*pq);
int QueueSize(Queue*pq);

这是我们对应的链表的接口，分别代表：队列初始化，队列销毁，队列插入，队列删除，找到队列的头，找到队列的尾，判断队列是否为空，返回队列的元素个数。

队列的初始化：

void QueueInit(Queue*pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

队列的销毁：

void QueueDestory(Queue*pq)
{
	assert(pq);
	QNode*cur = pq->head;
	while (cur)
	{
		QNode*del = cur;
		cur = cur->next;
		free(del);
	}
	pq->head = pq->tail = NULL;
}

我们画图进行分析：

 我们把cur赋给队列的头，然后进行遍历，把cur->next赋给cur，然后释放掉cur，直到cur=NULL。

接下来，我们来实现队列的插入：

void QueuePush(Queue*pq, QDataType x)
{
	assert(pq);
	QNode*newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->next = NULL;
	}
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

我们首先来分析代码：

QNode*newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

用动态内存的知识创建一个新的节点，如果动态内存申请失败，打印对应的错误信息，退出程序。

else
	{
		newnode->data = x;
		newnode->next = NULL;
	}

如果创建成功的话，newnode对应的值赋为x，并把他的下一位置为空指针。

if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}

假如pq->tail为空指针，就表示队列中没有其他的元素，那么队列的头和队列的尾就相同。

else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

假如队列中本身就有元素，那么就在队尾尾插一个newnode节点。

我们画图象进行解释：

 

 然后把newnode置为tail

接下来，我们来讲删除队列元素

我们首先来绘制图像：

因为我们的队列只能够进行头删元素。

然后把我们的head'后置

 

然后释放掉del

 

 我们编写代码进行尝试：

void QueuePop(Queue*pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode*del = pq->head;
		pq->head = pq->head->next;
		free(del);
		del = NULL;
	}
}

assert(!QueueEmpty(pq));

这里表示我们需要鉴别队列是否为空，当队列为空的时候，我们是无法删除元素的，所以我们要进行断言。

if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}

这里是特殊情况，假如我们删除的是最后一个元素：

 然后我们释放掉最后一个元素。

 我们的tail就形成了野指针，所以我们要分情况

当队列中只有一个元素时，我们释放掉该元素，然后把链表全部置为空。

当链表有多个元素的时候：

else
	{
		QNode*del = pq->head;
		pq->head = pq->head->next;
		free(del);
		del = NULL;
	}

取队头和队尾的数据：

QDataType QueueFront(Queue*pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}
QDataType QueueBack(Queue*pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

判断队列是否为空

bool QueueEmpty(Queue*pq)
{
	assert(pq);
	return pq->head == NULL&&pq->tail == NULL;
}

查找链表的元素：

int QueueSize(Queue*pq)
{
	assert(pq);
	QNode*cur = pq->head;
	int n = 0;
	while (cur)
	{
		++n;
		cur = cur->next;
	}
	return n;
}