-
【优化器】BGD、SGD、MSGD、Momentum、Adagrad、RMSPprop、Adam
一、优化器介绍
1、梯度下降法
梯度下降法有三种不同的形式:
- BGD(Batch Gradient Descent):批量梯度下降,每次训练使用 所有样本
- SGD(Stochastic Gradient Descent):随机梯度下降,每次训练只使用 1个样本
- MBGD(Mini-Batch Gradient Descent):小批量梯度下降,每次训练参数使用小部分数据样本(mini_batch)
这三个优化算法在训练的时候虽然所采用的的数据量不同,但是他们在进行参数优化的时候,采用的方法是相同的
在训练的时候一般都是使用小批量梯度下降算法,即选择部分数据进行训练,这里把这三种算法统称为传统梯度下降法,因为他们在更新参数的时候采用相同的方式,而更优的优化算法从 梯度方面 和 学习率方面 对参数更新方式进行优化
传统梯度更新算法为最常见、是最简单的一种参数更新策略。
其基本思想是:先设定一个学习率 λ \lambda λ,参数沿梯度的反方向移动。假设需要更新的参数为 θ \theta θ,梯度为 g g g,则其更新策略可表示为:
θ ← θ − η ∗ g \theta \leftarrow \theta - \eta * g θ←θ−η∗g优点:
- 算法简洁,当学习率取值恰当时,可以收敛到 全局最优点(凸函数) 或 局部最优点(非凸函数)。
缺点:
- 对超参数学习率比较敏感:过小导致收敛速度过慢,过大又越过极值点
- 学习率除了敏感,有时还会因其在迭代过程中保持不变,很容易造成算法被卡在鞍点的位置。
- 在较平坦的区域,由于梯度接近于0,优化算法会因误判,在还未到达极值点时,就提前结束迭代,陷入局部极小值。
1.1 一维梯度下降法
我们以 目标函数(损失函数) f ( x ) = x 2 f(x)= x^2 f(x)=x2 为例来看一看梯度下降是如何工作的。
迭代方法为:
x ← x − η ∗ g = x − η ∗ ∂ l o s s ∂ x x \leftarrow x - \eta * g = x - \eta * \frac{\partial loss}{\partial x} x←x−η∗g=x−η∗∂x∂loss虽然我们知道最小化 f(x) 的解为x=0 ,这里依然使用这个简单函数来观察 x 是如何被迭代的
这里x为模型参数,使用x = 10 作为初始值,并设 学习率 e t a = 0.2 eta = 0.2 eta=0.2,使用梯度下降法 对x 迭代10次
import numpy as np import matplotlib.pyplot as plt x = 10 lr = 0.2 result = [x] for i in range(10): x -= lr * 2 * x result.append(x) f_line = np.arange(-10, 10, 0.1) plt.plot(f_line, [x * x for x in f_line]) plt.plot(result, [x * x for x in result], '-o') plt.title('learning rate = {}'.format(lr)) plt.xlabel('x') plt.ylabel('f(x)') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18

大家可以尝试使用不同的学习率进行训练,会得到如下结果:

- 如果使用的学习率太小,将导致 x x x的更新非常缓慢,需要更多的迭代。
- 相反,当使用过大的学习率, x x x的迭代不能保证降低 f ( x ) f(x) f(x) 的值,例如,当学习率为 η = 1.1 \eta=1.1 η=1.1时, x x x超出了最优解 x = 0 x=0 x=0,并逐渐发散
1.2 多维梯度下降法
在对一元梯度下降有了了解之后,下面看看多元梯度下降,即考虑 X = [ x 1 , x 2 , ⋯ x d ] T X=[x_1, x_2, \cdots x_d]^T X=[x1,x2,⋯xd]T 的情况。
多元损失函数,它的梯度也是多元的,是一个由d个偏导数组成的向量:
∇ f ( X ) = [ ∂ f x ∂ x 1 , ∂ f x ∂ x 2 , ⋯ , ∂ f x ∂ x d ] T \nabla f(X) = [\frac{\partial f_x}{\partial x_1}, \frac{\partial f_x}{\partial x_2}, \cdots, \frac{\partial f_x}{\partial x_d}]^T ∇f(X)=[∂x1∂fx,∂x2∂fx,⋯,∂xd∂fx]T然后选择合适的学率进行梯度下降:
θ ← θ − η ∗ ∇ f ( X ) \theta \leftarrow \theta - \eta * \nabla f(X) θ←θ−η∗∇f(X)下面通过代码可视化它的参数更新过程。构造一个目标函数 f ( X ) = x 1 2 + 2 x 2 2 f(X)=x_1^2+2x_2^2 f(X)=x12+2x22,并有二维向量 X = [ x 1 , x 2 ] X = [x_1, x_2] X=[x1,x2]作为输入,标量作为输出。 损失函数的梯度为 ∇ f ( x ) = [ 2 x 1 , 4 x 2 ] T \nabla f(x) = [2x_1,4x_2]^T ∇f(x)=[2x1,4x2]T 。使用梯度下降法,观察 x 1 , x 2 x_1, x_2 x1,x2从初始位置[-5, -2] 的更新轨迹。
import numpy as np import matplotlib.pyplot as plt def loss_func(x1, x2): #定义目标函数 return 0.1 * x1 ** 2 + 2 * x2 ** 2 x1, x2 = -5, -2 eta = 0.4 num_epochs = 20 result = [(x1, x2)] for epoch in range(num_epochs): gd1 = 0.2 * x1 gd2 = 4 * x2 x1 -= eta * gd1 x2 -= eta * gd2 result.append((x1, x2)) # print('x1:', result1) # print('\n x2:', result2) plt.plot(*zip(*result), '-o', color='#ff7f0e') x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1)) plt.contour(x1, x2, loss_func(x1, x2), colors='#1f77b4') plt.title('learning rate = {}'.format(eta)) plt.xlabel('x1') plt.ylabel('x2') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
2、动量(Momentum)
动量算法每下降一步都是由前面下降方向的一个累积和当前点梯度方向组合而成:
累计梯度更新: v ← α v + ( 1 − α ) g 累计梯度更新:v \leftarrow \alpha v + (1 - \alpha)g 累计梯度更新:v←αv+(1−α)g 梯度更新: x θ ← θ − η ∗ v 梯度更新: x\theta \leftarrow \theta - \eta*v 梯度更新:xθ←θ−η∗v α 为动量参数, v 累计梯度, η 为学习率 \alpha 为动量参数,v累计梯度,\eta 为学习率 α为动量参数,v累计梯度,η为学习率为了更好的观察动量带来的好处,我们使用一个新函数 f ( x ) = 0.1 x 1 2 + 2 x 2 2 f(x)=0.1x_1^2+2x_2^2 f(x)=0.1x12+2x22 ,这里 x 1 x_1 x1和 x 2 x_2 x2的系数分别是 0.1 和 2, 这就使得 x 1 x_1 x1和 x 2 x_2 x2 的梯度值相差一个量级,如果使用相同的学习率, x 2 x_2 x2 的更新幅度会较 x 1 x_1 x1 的更大些。
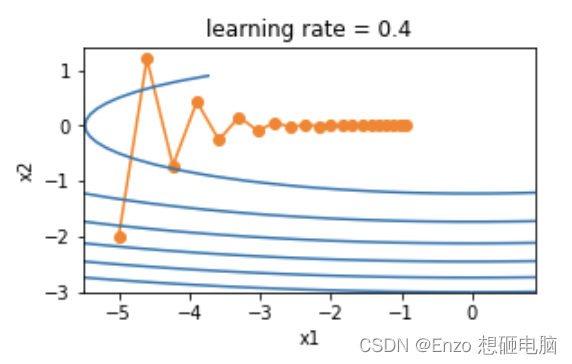
我们先使用不带动量的传统梯度下降算法观察其下降过程,学习率设置为 0.4
import numpy as np import matplotlib.pyplot as plt def loss_func(x1, x2): #定义目标函数 return 0.1 * x1 ** 2 + 2 * x2 ** 2 x1, x2 = -5, -2 eta = 0.4 num_epochs = 20 result = [(x1, x2)] for epoch in range(num_epochs): gd1 = 0.2 * x1 gd2 = 4 * x2 x1 -= eta * gd1 x2 -= eta * gd2 result.append((x1, x2)) plt.plot(*zip(*result), '-o', color='#ff7f0e') x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1)) plt.contour(x1, x2, loss_func(x1, x2), colors='#1f77b4') plt.title('learning rate = {}'.format(eta)) plt.xlabel('x1') plt.ylabel('x2') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
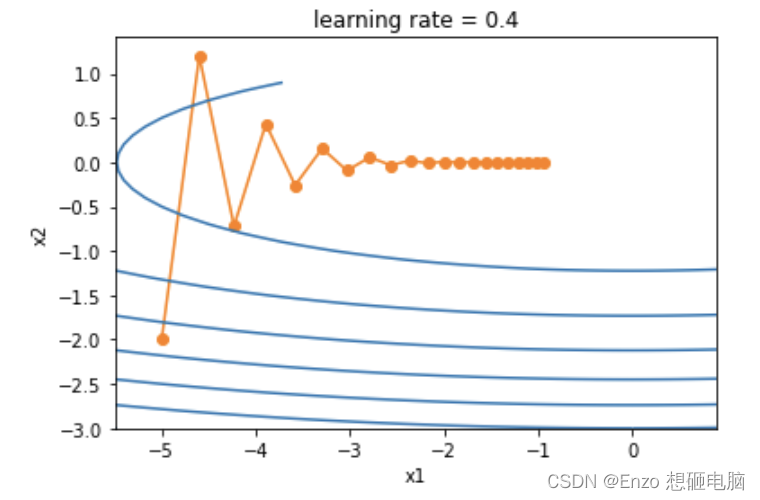
从结果来看,和我们预料的一样:使用相同的学习率, x 2 x_2 x2 的更新幅度会较 x 1 x_1 x1 的更大些,变化快得多。接下来,我们依然使用传统梯度下降算法,将学习率设置为 0.6。
因为 x 2 的更新路径如下,这会导致 x_2的更新路径如下,这会导致 x2的更新路径如下,这会导致x_2$的值越来越发散:
x 2 = x 2 − η ∗ g d 2 = x 2 − 0.6 ∗ ( 4 ∗ x 2 ) = − 1.4 x 2 x_2 = x_2 - \eta * gd_2 = x_2 - 0.6 *(4* x_2) = -1.4x_2 x2=x2−η∗gd2=x2−0.6∗(4∗x2)=−1.4x2更新过程如下图:
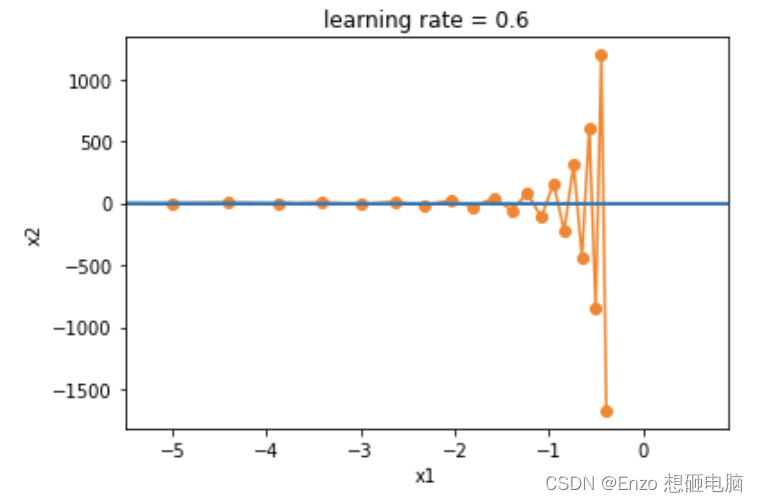
这时,我们会陷入一个两难的选择:- 如果选择较小的准确率。可以确保不会朝 x 2 x_2 x2方向发生偏离,但在 x 1 x_1 x1方向收敛会缓慢。
- 如果选择较大的准确率,
x
1
x_1
x1方向会收敛很快,但在
x
2
x_2
x2方向就不会向最优点靠近。下面将
学习率从0.4调整到0.6。可以看出在X1方向会有所改善,但是整体解决方案会很差。
有没有什么方法解决这个问题呢?
下面我们尝试从改变梯度入手,将历史的梯度考虑在内:
累计梯度更新: v ← α v + ( 1 − α ) g 累计梯度更新:v \leftarrow \alpha v + (1 - \alpha)g 累计梯度更新:v←αv+(1−α)g
梯度更新: θ ← θ − η ∗ v 梯度更新: \theta \leftarrow \theta - \eta*v 梯度更新:θ←θ−η∗v
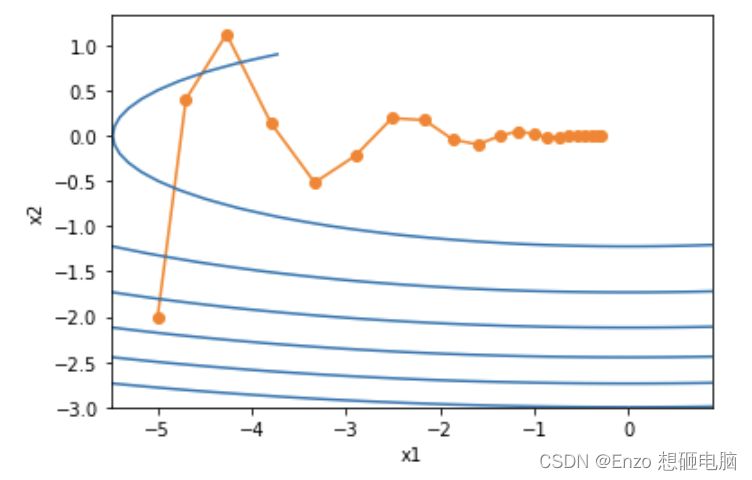
α \alpha α 为动量参数, v v v是累计梯度, η \eta η 为学习率下面我们使用带动量的梯度算法,将学习率设置为 0.4
%matplotlib inline import numpy as np import matplotlib.pyplot as plt def loss_func(x1, x2): #定义目标函数 return 0.1 * x1 ** 2 + 2 * x2 ** 2 x1, x2 = -5, -2 v1, v2 = 0, 0 eta, alpha = 0.4, 0.5 num_epochs = 20 result = [(x1, x2)] for epoch in range(num_epochs): v1 = alpha * v1 + (1 - alpha) * (0.2 * x1) v2 = alpha * v2 + (1 - alpha) * (4 * x2) x1 -= eta * v1 x2 -= eta * v2 result.append((x1, x2)) plt.plot(*zip(*result), '-o', color='#ff7f0e') x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1)) plt.contour(x1, x2, loss_func(x1, x2), colors='#1f77b4') plt.xlabel('x1') plt.ylabel('x2') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30

即使我们将学习率设置为0.6, x 2 x_2 x2 的梯度也不会发散了
3、NAG
4、Adagrad
5、RMSProp
6、Adam
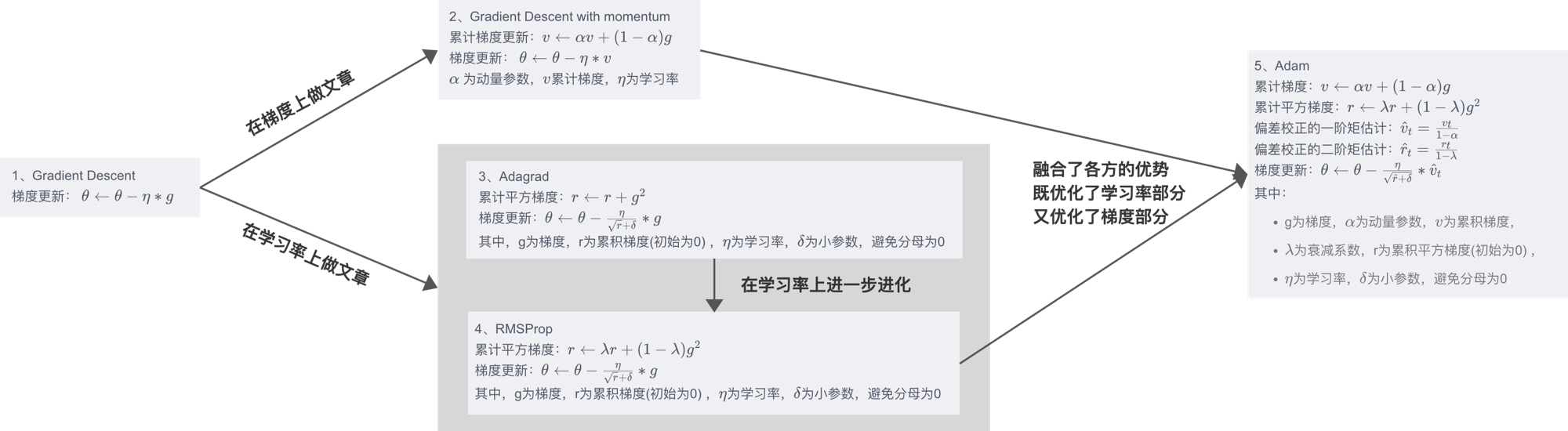
7、总结:
1、Gradient Descent
梯度更新: θ ← θ − η ∗ g \theta \leftarrow \theta - \eta*g θ←θ−η∗g2、Gradient Descent with momentum
累计梯度更新: v ← α v + ( 1 − α ) g v \leftarrow \alpha v + (1 - \alpha)g v←αv+(1−α)g
梯度更新: θ ← θ − η ∗ v \theta \leftarrow \theta - \eta*v θ←θ−η∗v
α \alpha α 为动量参数, v v v累计梯度, η \eta η为学习率3、Adagrad
累计平方梯度: r ← r + g 2 r \leftarrow r + g^2 r←r+g2
梯度更新: θ ← θ − η r + δ ∗ g \theta \leftarrow \theta - \frac{\eta}{\sqrt {r + \delta}}*g θ←θ−r+δη∗g
其中,g为梯度,r为累积平方梯度(初始为0) , η \eta η为学习率, δ \delta δ为小参数,避免分母为04、RMSProp
累计平方梯度: r ← λ r + ( 1 − λ ) g 2 r \leftarrow \lambda r + (1 - \lambda)g^2 r←λr+(1−λ)g2
梯度更新: θ ← θ − η r + δ ∗ g \theta \leftarrow \theta - \frac{\eta}{\sqrt {r + \delta}}*g θ←θ−r+δη∗g
其中,g为梯度,r为累积平方梯度(初始为0) , η \eta η为学习率, δ \delta δ为小参数,避免分母为05、Adam
累计梯度: v ← α v + ( 1 − α ) g v \leftarrow \alpha v + (1 - \alpha)g v←αv+(1−α)g
累计平方梯度: r ← λ r + ( 1 − λ ) g 2 r \leftarrow \lambda r + (1 - \lambda)g^2 r←λr+(1−λ)g2
偏差校正的一阶矩估计: v ^ t = v t 1 − α \hat{v}_t = \frac{v_t}{1 - \alpha} v^t=1−αvt
偏差校正的二阶矩估计: r ^ t = r t 1 − λ \hat{r}_t = \frac{r_t}{1 - \lambda} r^t=1−λrt
梯度更新: θ ← θ − η r ^ + δ ∗ v ^ t \theta \leftarrow \theta - \frac{\eta}{\sqrt {\hat{r} + \delta}}*\hat{v}_t θ←θ−r^+δη∗v^t
其中:- g为梯度, α \alpha α为动量参数, v v v为累积梯度,
- λ \lambda λ为衰减系数,r为累积平方梯度(初始为0) ,
- η \eta η为学习率, δ \delta δ为小参数,避免分母为0
二、动态修改学习率参数
修改参数的方式可以通过修改参数optimizer.params_groups或新建optimizer。新建
optimizer比较简单,optimizer 十分轻量级,所以开销很小。但是新的优化器会初始化动量
等状态信息,这对于使用动量的优化器(momentum参数的sgd)可能会造成收敛中的震
荡。所以,这一般采用修改参数optimizer.params_groups查看优化器的参数,有8个参数
print(optimizer.param_groups[0].keys()) 输出: dict_keys(['params', 'lr', 'momentum', 'dampening', 'weight_decay', 'nesterov', 'maximize', 'foreach'])- 1
- 2
- 3
- 4
用pycharm查看:
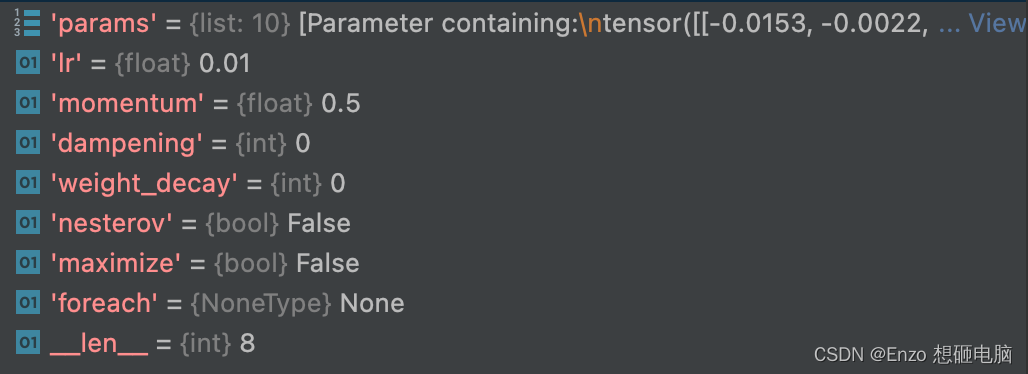
我们可以通过动态修改参数 “lr” 的值,来实现动态参数的调整:
比如,我们想要每 5个 epoch 修改一次学习率,改为之前学习率的 0.1 倍if epoch % 5 == 0: optimizer.param_groups[0]['lr'] *= 0.1- 1
- 2
-
相关阅读:
华为防火墙基本原理工作方法总结
TS的类型规则 类型排名
redis场用命令及其Java操作
马化腾2021年薪为4410万元,同比下降25%;淘宝支持修改账号名;Rust 1.60.0发布|极客头条
Python课程设计之学生信息管理系统
经典机器学习方法(4)—— 感知机
Mozilla Firefox侧边栏和垂直标签在131 Nightly版本中开始试用
vue表单及修饰符,vue事件,方法
关于SpringSecurity自定义方法权限
关于vue中image控件,onload事件里,event.target 为null的奇怪问题探讨
- 原文地址:https://blog.csdn.net/weixin_37804469/article/details/126157835
