-
Loj#3320-「CCO 2020」旅行商问题
正题
题目大意
有一张 n n n个点的无向完全图,每一条边是红色或者蓝色,对于每个点 s s s求从这个点出发的一条尽量短的经过所有点的路径。
1 ≤ n ≤ 2000 1\leq n\leq 2000 1≤n≤2000
解题思路
显然地猜测一下最短的长度肯定是 n n n,说是找一条路径,实际上我们是能够找到一个颜色交替只有一次的环的,然后交替位置就在 s s s的旁边。
我们构造一下,此时有两条不相交的路径 s → x , t → y s\rightarrow x,t\rightarrow y s→x,t→y,并且两条路径上颜色都相同,一条红色一条蓝色。
我们假设 s → x s\rightarrow x s→x的路径是红色,此时对于一个未加入的点 z z z,如果 ( x , z ) (x,z) (x,z)是红色或者 ( y , z ) (y,z) (y,z)是蓝色那么直接加长路径即可。
否则也就是说 ( x , z ) (x,z) (x,z)是蓝色且 ( y , z ) (y,z) (y,z)是红色,我们考虑 ( x , y ) (x,y) (x,y)之间的路径颜色,假设是红色,那么如图
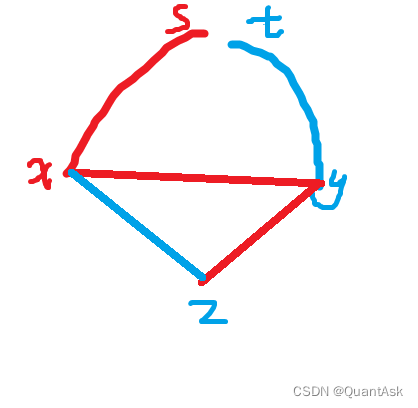
我们将 y y y弹出路径 t → y t\rightarrow y t→y,然后加入 s → x s\rightarrow x s→x后就可以再加入 z z z了。如果是蓝色同理弹另一边。
但是此时会出现两种情况:
- 蓝色路径弹出后为空了,那么此时我们再找一个新的点当做新的 t t t即可,反正我们的要求是 s s s不变。
- 红色路径弹出后为空了,那么此时我们将 z z z作为新的 t t t,然后原本的 s → t s\rightarrow t s→t路径变为 s → x s\rightarrow x s→x路径。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
code
#include#include #include #include using namespace std; const int N=2100; int n,G[N][N]; char s[N]; vector<int>l,r; int main() { scanf("%d",&n); if(n==2){ printf("2\n1 2\n2\n2 1\n"); return 0; } for(int i=2;i<=n;i++){ scanf("%s",s+1); for(int j=1;j<i;j++) G[i][j]=G[j][i]=(s[j]=='R'); } for(int s=1;s<=n;s++){ int z=s%n+1,g=0;l.clear();r.clear(); l.push_back(z);r.push_back(s);g=G[s][z%n+1]; for(int x=z%n+1;x!=s;x=x%n+1){ if(G[r[r.size()-1]][x]==g)r.push_back(x); else if(G[l[l.size()-1]][x]==!g)l.push_back(x); else{ if(G[l[l.size()-1]][r[r.size()-1]]==g){ r.push_back(l[l.size()-1]); r.push_back(x);l.pop_back(); if(!l.size()){ x=x%n+1;if(x==s)break; l.push_back(z=x); } } else{ l.push_back(r[r.size()-1]); l.push_back(x);r.pop_back(); if(!r.size()){ l.pop_back();l.swap(r); l.push_back(x);z=x;g=!g; } } } } printf("%d\n",n); for(int i=0;i<r.size();i++)printf("%d ",r[i]); for(int i=l.size()-1;i>=0;i--)printf("%d ",l[i]); putchar('\n'); } return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
-
相关阅读:
DSP篇--C6678功能调试系列之Nor_FLASH调试
linux 进程管理命令
【Java中23种面试常考的设计模式之代理模式(Proxy)---结构型模式】
【Linux修炼】5.vim详解
ICMP报文
hadoop -hive 安装
ubuntu18.04安装gtsam
MYSQL安装
前端基础建设与架构04 横向对比主流构建工具,了解构建工具的设计考量
Django(二)精美博客搭建(11)实现文章列表分页查询及首页简单优化
- 原文地址:https://blog.csdn.net/Mr_wuyongcong/article/details/126291100
