集合论基础

1.集合的初见

1.1 集合定义

什么是集合：

集合：由指定范围内满足特定条件的所有对象聚集在一起构成，每一个对象称为这个集合的元素。

公理化集合论：

外延公理 + 空集存在公理 + 无序对公理 + 并集公理 + 幂集公理 + 无穷公理 + 替换公理 + 正则公理 + 选择公理。(ZFC 公理化集合论)

这些公理描述的都是集合的一些属性

集合的例子：

1.2 集合的表示

集合的表示法：

• 大写字母$A,B,C...,A_1,A_2,C_1$表示集合
• 小写字母$a,b,c...,a_1,b_1,c_1,...$表示集合中的元素

属于关系：

a是集合A中的元素，则称a属于A，记为$a\in A$

若a不是集合A中的元素，则称a不属于A，记为$a\notin A$

集合的表示法：

• 枚举法： A = { a , b , c , d } , B = { 2 , 4 , 6 , 8 , 10.... } A=\{a,b,c,d\},B=\{2,4,6,8,10....\} A={a,b,c,d},B={2,4,6,8,10....}

• 叙述法：刻画集合中元素的特性表示集合 P = { x ∣ P ( x ) } P=\{x|P(x)\} P={x∣P(x)}

  A = { x ∣ x 是英文字母中的元音字母 } B = { x ∣ x ∈ Z , x < 10 } C = { x ∣ x = 2 k , k ∈ N } A=\{x|x是英文字母中的元音字母\}\\ B= \{x|x∈Z, x< 10\}\\ C=\{x|x= 2k,k∈N\} A={x∣x是英文字母中的元音字母}B={x∣x∈Z,x<10}C={x∣x=2k,k∈N}

• 文视图：用平面上的点做成图示

1.3 基数

集合包含的元素的数量称为集合的基数（base number），记为$|A|$

若一个集合的基数是有限的，则称该集合为有限集

若一个集合的基数是无限的，则称该集合为无限集

2.特殊集合与集合间的关系

2.1 空集

不含任何元素的集合称为空集，记做$\varnothing$

空集可以符号化为： ∅ = { x ∣ x ≠ x } \empty = \{x|x\neq x\} ∅={x∣x=x}

空集是绝对唯一的

2.2 全集

针对一个具体范围,我们考虑的所有对象的集合叫做全集(universal set) ,记作U或E.在文氏图一般使用方形表示全集。

2.3 相等关系

2.3.1 元素的基本特性

集合中的元素是无序的。

集合中的元素是不同的。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SFCNZe44-1660208238560)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220809232416396.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rQQmAYYV-1660208238560)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220809232442290.png)]

2.3.2 集合的外延性公里

集合的外延性原理

两个集合相等，当且仅当他们的元素完全相同，记为A=B，否则A和B不相等，记为$A\ne B$

2.4 包含关系

2.4.1 包含关系的定义

A中含有B中的所有元素，这种情况称为A包含B

$$"\subseteq ”关系的数学语言描述为：B\subseteq A\iff 对\forall x，如果x\in B，那么x\in A$$

2.4.2 集合相等与包含关系

证明集合相等：

设A和B为两个任意的集合，则$A=B\iff A\subseteq B并且B\subseteq A$【important】

2.4.3 n元集合的子集

n元集合的子集：

★推广:对于任意n元集合A，它的m元(0≤m≤n)子集个数为$C_n^m$个，所以不同的子集个数为: $C_n^0+C_n^1+...+C{n}^n=(1+1{)}^n=2^n$.

2.5 幂集

定义：设A为任意集合，把A所有不同的子集构成的集合称为A的幂集，记做$P(A)$，即：
P ( A ) = { x ∣ x ⊆ A } P(A) = \{x|x\sube A\} P(A)={x∣x⊆A}
幂集也叫作集族或集合的集合，对于集族的研究在数学方面，知识库和表处理语言以及人工智能等方面都有重要的意义。
$$x\in P(A)\iff x\subseteq A$$

3. 集合的运算

3.1 并集

3.2 交集

3.3 补集

3.4 差集

3.5 对称差集

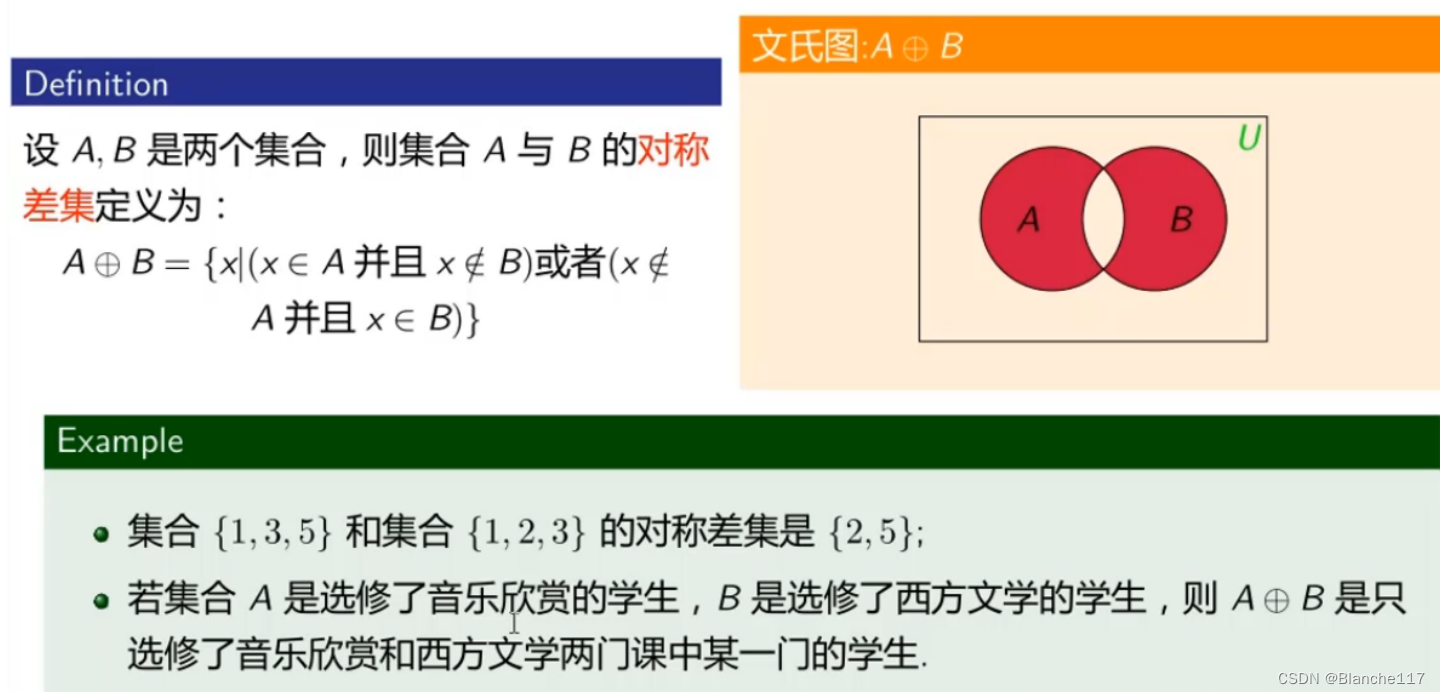
4.集合的运算定律

4.1 运算定律

幂等律：$A\cup A=A;A\cap A=A$

交换律：$A\cup B=B\cup A;A\cap B=B\cap A$

结合律：$A\cup (B\cup C)=(A\cup B)\cup C,A\cap (B\cap C)=(A\cap B)\cap C$

同一律：$A\cup \varnothing =A,A\cap U=A$.

零律：$A\cup U=U,A\cap \varnothing =\varnothing$.

分配律： $A\cup (B\cap C)=(A\cup B)\cap (A\cup C),A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$.——与加减法不同，并也满足分配

吸收律： $A\cup (A\cap B)=A,A\cap (A\cup B)=A$.

矛盾律和排空律： $\bar{A}\cap A=\varnothing ,\bar{A}\cup A=U$.

双重否定律：$\overline{\overline{A}}=A$

德摩根律：$\overline{A\cup B}=\bar{A}\cap \overline{B},\overline{A\cap B}=\overline{A}\cup \overline{B}$.

4.2 证明

证明方法：

5.可数集合和不可数集合

5.1 自然数集

5.1.1 皮亚诺公里

皮亚诺公理：基于序数的自然数定义公理。定理包括：

• 0是自然数
• 每个自然数n都有一个后继，这个后继也是一个自然数，记为$S(n)$
• 两个自然数相等，当且仅当他们有相同的后继，即$m=n$，当且仅当$S(m)=S(n)$
• 没有任何自然数的后继是0
• （归纳公理）若$\phi$是一个自然数的预测
  • 如果$\phi (0)$为真
  • 当$\phi (n)$为真，则有$\phi (S(n))$为真
  • 则$\phi (n)$对任何自然数成立

5.1.2 冯诺依曼的自然数定义

5.2 等势

如何比较集合之间元素的多少？

• 有限集合：基数
• 无限集合：看集合之间是否存在一种一一对应关系【等势】

设A，B为两个集合，若A，B之间存在一种一一对应关系：
$$\Psi :A\to B$$
则称A和B是等势的，记做：
$$A\sim B$$

note：由等势的定义可以看出，如果 A = B，那么$A\sim B$，反之不成立

5.3 可数集合

凡是与自然数集合等势的集合，称为可数集合（countable set），该集合的基数记为${\aleph }_0$（读作阿列夫0）

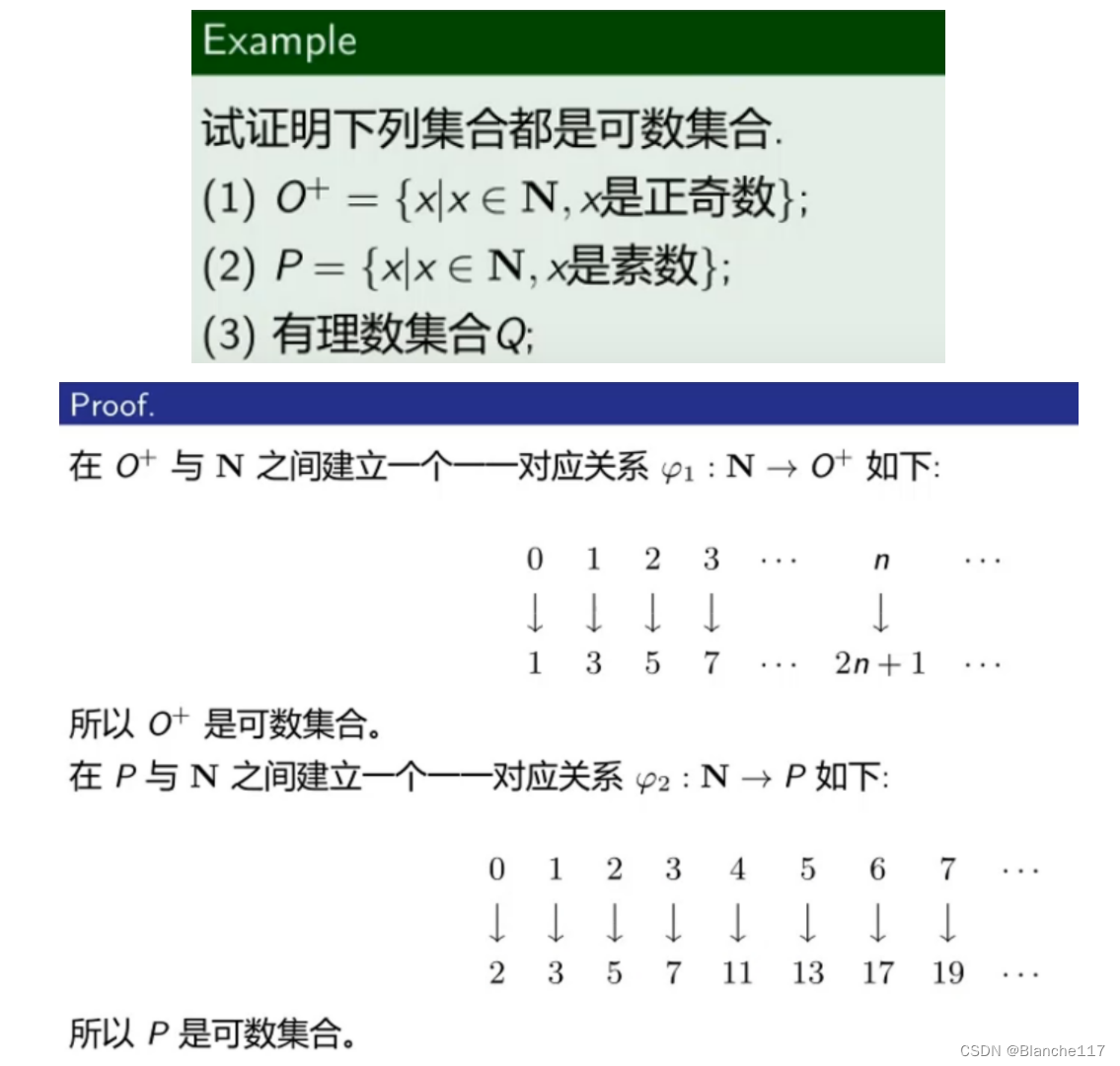
• 两个无限集合的大小不能用集合中的元素的个数来衡量，${\aleph }_0$表示一切可数集合的基数，是一种抽象的表达
• 表面上个数完全不相等的两个集合之间仍然可能存在等势关系，如集合与其真子集之间，体现了有限集合和无限集合的根本差别

5.4 不可数集合

定义：开区间$(0,1)$称为不可数集合，凡是与开区间$(0,1)$等势的集合，称为不可数集合，该集合的基数记为$\aleph$（读作阿列夫）