题目描述

题面翻译

• 给定一个长度为 $n$ 的序列 $a_{1\dots n}$。
• 你要求一个 $a$ 的子序列 $b_{1\dots m}$（可以为空），使得 ${\sum }_{i=1}^{m}i{b}_i$ 的值最大。
• $n\le 10^5$，$|a_i|\le 10^7$。
• 时间限制：6秒。

题目描述

Limak is an old brown bear. He often goes bowling with his friends. Today he feels really good and tries to beat his own record!

For rolling a ball one gets a score — an integer (maybe negative) number of points. Score for $i$ -th roll is multiplied by $i$ and scores are summed up. So, for $k$ rolls with scores $s_1,s_2,...,s_k$ , total score is 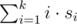. Total score is $0$ if there were no rolls.

Limak made $n$ rolls and got score $a_i$ for $i$ -th of them. He wants to maximize his total score and he came up with an interesting idea. He will cancel some rolls, saying that something distracted him or there was a strong wind.

Limak is able to cancel any number of rolls, maybe even all or none of them. Total score is calculated as if there were only non-canceled rolls. Look at the sample tests for clarification. What maximum total score can Limak get?

输入格式

The first line contains single integer $n$ ($1<=n<=10^5$ ).

The second line contains $n$ space-separated integers $a_1,a_2,...,a_n$ ($|a_i|<=10^7)$ - scores for Limak’s rolls.

输出格式

Print the maximum possible total score after choosing rolls to cancel.

样例 #1

样例输入 #1

5
-2 -8 0 5 -3
1
2

样例输出 #1

13
1

样例 #2

样例输入 #2

6
-10 20 -30 40 -50 60
1
2

样例输出 #2

400
1

提示

In first sample Limak should cancel rolls with scores $-8$ and $-3$ . Then he is left with three rolls with scores $-2,0,5$ . Total score is $1\cdot (-2)+2\cdot 0+3\cdot 5=13$ .

In second sample Limak should cancel roll with score $-50$ . Total score is $1\cdot (-10)+2\cdot 20+3\cdot (-30)+4\cdot 40+5\cdot 60=400$ .

算法思想（动态规划）

状态表示

$f[i][j]$表示在数列的前$i$个数中已经选择$j$个数时的最大值。

状态计算

f [ i ] [ j ] = m a x { f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − 1 ] + j ∗ x i , f [ i − 1 ] [ j − 2 ] + ( j − 1 ) ∗ x i , . . . , f [ i − 1 ] [ 1 ] + 2 ∗ x i , f [ i − 1 ] [ 0 ] + x i } f[i][j]=max\{f[i-1][j], f[i-1][j-1]+j*x_i,f[i-1][j-2]+(j-1)*x_i,...,f[i-1][1]+2*x_i,f[i-1][0]+x_i\} f[i][j]=max{f[i−1][j],f[i−1][j−1]+j∗xi​,f[i−1][j−2]+(j−1)∗xi​,...,f[i−1][1]+2∗xi​,f[i−1][0]+xi​}，其中$j<=i$。

由于第$i$阶段的状态只与$i-1$阶段的状态有关，因此可以进行状态优化，使用一维状态进行计算，即 f [ j ] = m a x { f [ j ] , f [ j − 1 ] + j ∗ x i , f [ j − 2 ] + ( j − 1 ) ∗ x i , . . . , f [ 1 ] + 2 ∗ x i , f [ 0 ] + x i } f[j] = max\{f[j], f[j-1]+j*x_i,f[j-2]+(j-1)*x_i,...,f[1]+2*x_i,f[0]+x_i\} f[j]=max{f[j],f[j−1]+j∗xi​,f[j−2]+(j−1)∗xi​,...,f[1]+2∗xi​,f[0]+xi​}

需要注意的是，在计算第$i$阶段的状态时，只能使用$i-1$阶段的状态，为了防止状态污染，需要从大到小枚举$j$。

如果从小到大枚举$j$，那么在计算$f[j]$之前，$f[j-1]$将会被更新为第$i$阶段的状态，与优化之前不符，称为状态污染。

初始状态

由于数列中存在负数，因此求最大值时，f[j]应输出化为$-\infty$；除此之外，$f[0]=0$。

代码实现

#include 
#include 
using namespace std;
typedef long long LL;
const int N = 100010;
LL f[N];
int main()
{
    LL n, x;
    scanf("%lld", &n);
    memset(f, 0xbf, sizeof f); //将f初始化为无穷小
    f[0] = 0;
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%lld", &x);
        for(int j = i; j > 0; j --)
            f[j] = max(f[j], f[j - 1] + j * x);
    }
    LL ans = -1e18;
    for(int i = 1; i <= n; i ++) ans = max(ans, f[i]);
    printf("%lld", ans);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23