题目描述

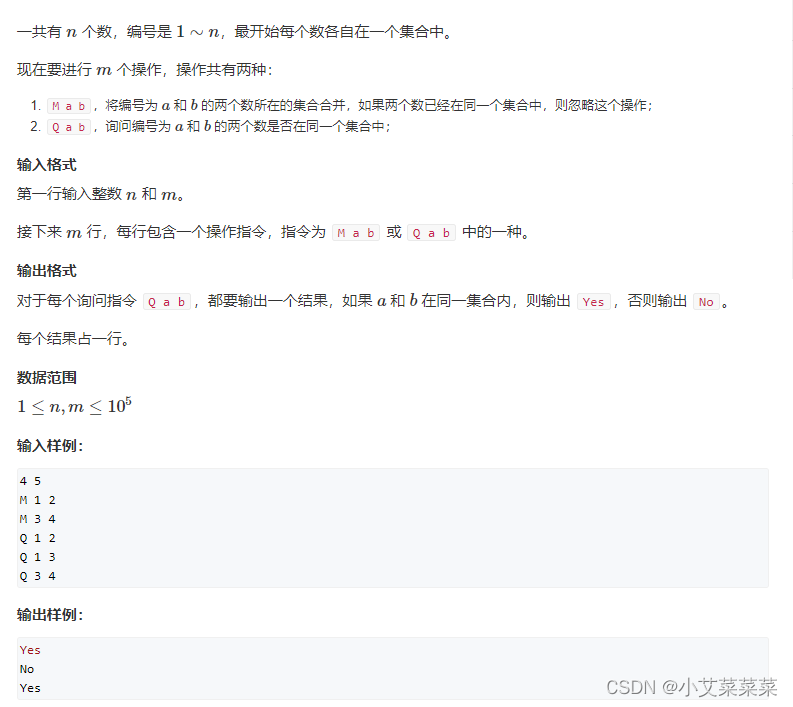
思路

并查集
从代码的角度分析

首先初始化

for ( int i = 0; i < 8; i ++ ) p[i] = i;

上面的代码就是实现了如下图所示的结果：

不难理解，就是将当前的数据的父结点指向自己

查找 + 路径压缩

//这是返回 x 的父节点与 + 路径压缩
int find(int x )
{
//而祖先节点的i局势父节点本身
if (p [ x ] != x )
{
//将 x 的父亲置为 x 的父亲的祖先节点，从而实现路径压缩
p [ x ] = find ( p [ x ] ) ;
}
return p [ x ] ;
}

find 的功能时用于查找祖先节点，那么路径压缩又是怎么完成的呢？

注意上图，当我们在查找 1 的父节点的过程中，路径压缩的实现

下面进行简单的模拟：
针对 x = 1

find(1) p[1] = 2 p[1] = find(2)
find(2) p[2] = 3 p[2] = find(3)
find(3) p[3] = 4 p[3] = find(4)
find(4) p[4] = 4 将p[4]返回

退到上一层
find(3) p[3] = 4 p[3] = 4 将p[3]返回
退到上一层
find(2) p[2] = 3 p[2] = 4 将p[2]返回
退到上一层
find(1) p[1] = 2 p[1] = 4 将p[1]返回

至此，我们发现所有的1，2，3的父节点全部置为了4，实现路径压缩；同时也实现了1的父节点的返回 nice!!

合并操作

if ( op [0] == 'M' ) p [ find ( a ) ] = find ( b ) ; 将实现 a 的祖先节点的父节点置为 b 的祖先节点
假设有俩个集合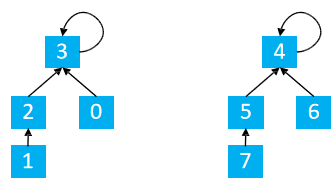

合并 1， 5
find(1) = 3 find(5 ) = 4
p[find(1)] = find(5) ---> p[3] = 4
如下图所示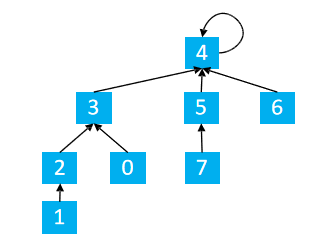

代码实现

#include 

using namespace std;

const int N = 100010;

int n, m;
int p[N];

int find(int x){ //返回x的祖先节点 + 路径压缩
    //祖先节点的父节点是自己本身
    if(p[x] != x){
        //将x的父亲置为x父亲的父亲,实现路径的压缩
        p[x] = find(p[x]);    
    }
    return p[x]; 
}

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++) p[i] = i; //初始化，让数x的父节点指向自己
    while(m --){
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);

        if(op[0] == 'M') p[find(a)] = find(b); //将a的祖先点的父节点置为b的祖先节点
        else{
            if(find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37