-
数据结构之八大排序——快速排序

目录
一、排序过程
在待排序表L[1...n]中任取一个元素pivot作为枢轴(通常情况下取第一个元素为枢轴),通过一趟排序将待排序表划分为独立的两部分L[1...k-1]和L[k+1...n],使得L[1...k-1]元素都小于pivot,L[k+1...n]元素都大于或等于pivot。
- 选取第一个元素为枢轴。
- j指针负责从右往左依次比较直到找到比基准点小的元素,此时i开始从左往右依次比较直到找到比基准点大的元素,一旦找到二者进行交换,直到i,j重合。
- 最后枢轴元素与i或j交换(此时i和j重合)。
二、代码
- public class QuickSort {
- public static void main(String[] args) {
- int[] arr = {3, 6, 4, 1, 9, 6, 5, 8, 7, 2};
- System.out.print("排序前为:");
- for (int i : arr) {
- System.out.print(i + " ");
- }
- System.out.println();
- quick(arr, 0, arr.length - 1);
- System.out.print("排序后为:");
- for (int i : arr) {
- System.out.print(i + " ");
- }
- }
- public static void quick(int[] arr, int low, int high) {
- if (low > high) {
- return;
- }
- //排序完枢轴的下标(将数组分为两部分)
- int k = quicksort(arr, low, high);
- //对第前面小于枢轴的元素进行递归排序
- quick(arr, low, k - 1);
- //对第后面大于枢轴的元素进行递归排序
- quick(arr, k + 1, high);
- }
- public static int quicksort(int[] arr, int low, int high) {
- int i = low;
- int j = high;
- //中间变量
- int temp;
- int pivot = arr[low];
- while (i < j) {
- //j从后往前找比枢轴小的元素
- while (i < j && arr[j] > pivot) {
- j--;
- }
- //i从前往后找比枢轴大的元素
- while (i < j && arr[i] <= pivot) {
- i++;
- }
- temp = arr[j];
- arr[j] = arr[i];
- arr[i] = temp;
- }
- //将枢轴元素和i或者j互换
- temp = arr[i];
- arr[i] = arr[low];
- arr[low] = temp;
- return j;
- }
- }
快速排序第一次划分:

结果:

三、性能及稳定性分析
1.空间复杂度
由于快速排序是递归的,需要借助一个递归工作栈来保存每层递归调用的必要信息,其容量应与递归调用的最大深度一致。最好情况下为O(
 );最坏情况是O(n),所以平均情况下空间复杂度为O(
);最坏情况是O(n),所以平均情况下空间复杂度为O( )。
)。2.时间复杂度
最坏情况下即对初始序列基本有序或者逆序的情况下,时间复杂度为O(
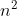 )。
)。有很多方法可以提高效率,如:取一个可以将数据平分的枢轴元素。
理想状态下,pivot可能做到平衡的划分,得到的两个子问题的大小都不可能大于n/2,在这种情况下快速排序的运行速度大大提升。
所以快速排序的平均时间复杂度是O(
 )
)3.稳定性
由上图对快速排序第一次划分的分析,黑色的6开始在前面红色的6在后面,而排完序后黑色的6在红色6的后面,当相同关键字的记录被划分到不同的子表时,可能会改变他们的顺序。因此快速排序是一个不稳定的排序。

-
相关阅读:
BP神经网络对指纹识别的应用(Matlab代码实现)
基于PHP+MySQL仓库管理系统的设计与实现
【C刷题】day5
Linux Podman安装DVWA靶场环境
CSS基本介绍
Linux 后台开发必知的 I/O 优化知识总结
[ 隧道技术 ] 反弹shell的集中常见方式(四)python反弹shell
第 46 届国际大学生程序设计竞赛(ICPC)亚洲区域赛(沈阳),签到题5题
c++的库函数std::move() 与 完美转发函数 std:: forward 源码
动手写数据库:实现记录管理
- 原文地址:https://blog.csdn.net/weixin_55166132/article/details/125838631
