-
洛谷 P5306 [COCI2019] Transport 题解
题目大意:
在一棵树中,找出满足条件的点对
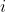 ,
,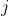 数量,使从
数量,使从 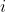 能走到
能走到 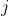 ,其中任意时刻,满足点权之和大于等于边权之和。
,其中任意时刻,满足点权之和大于等于边权之和。算法分析:
看题目的描述,很明显是一道点分治的题目。关键在于如何去维护答案。
这道题是我们的模拟赛题,考场上打了一个假到不能再假的点分治,一分没有。
先来模拟一下点分治的过程:首先找到
 ,对于根为
,对于根为  的这棵树进行操作,最后把
的这棵树进行操作,最后把 删掉。
删掉。那么这道题,很自然的难点,就是如何对这棵树进行操作,我们一步一步看。
首先,
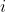 和
和 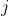 要在
要在  的两棵不同的子树中,最后统计答案的时候,把
的两棵不同的子树中,最后统计答案的时候,把 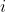 和
和 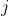 在一棵子树的情况给删掉就行。
在一棵子树的情况给删掉就行。关键操作:把
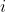 到
到 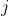 的路径,分为
的路径,分为 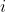 到
到  和
和  到
到 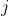 。我们用两个数组
。我们用两个数组 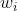 ,
,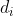 分别记录这条路径的点权之和,和边权之和。
分别记录这条路径的点权之和,和边权之和。第一步,从
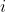 到
到  :对于满足条件的节点
:对于满足条件的节点 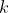 ,需要
,需要 ![w[i]-w[k] \geq d[i]-d[k]](https://1000bd.com/contentImg/2022/08/13/111705527.gif) ,把这个式子移项,可以得到
,把这个式子移项,可以得到 ![(w[i]-d[i])-(w[k]-d[k]) \geq 0](https://1000bd.com/contentImg/2022/08/13/111709128.gif) 。所以我们记录最大的
。所以我们记录最大的 ![w[k]-d[k]](https://1000bd.com/contentImg/2022/08/13/111710022.gif) 就可以判断
就可以判断 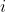 到
到  是否合法。
是否合法。第二步,从
 到
到 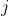 :这种情况,该路径的起点不一定是
:这种情况,该路径的起点不一定是  ,可以从另一个子树的
,可以从另一个子树的 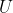 为起点。设以
为起点。设以 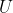 为起点到
为起点到  ,剩余的油量是
,剩余的油量是 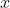 ,则路径上的任意一点
,则路径上的任意一点 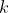 ,需要满足
,需要满足 ![x+w[fa[k]] \geq d[k]](https://1000bd.com/contentImg/2022/08/13/111716069.gif) ,fa[k] 表示 k 的父亲。变换一下,式子就变成
,fa[k] 表示 k 的父亲。变换一下,式子就变成 ![x+(w[fa[k]]-d[k]) \geq 0](https://1000bd.com/contentImg/2022/08/13/111716853.gif) 。这时我们维护路径上
。这时我们维护路径上 ![w[fa[k]]-d[k]](https://1000bd.com/contentImg/2022/08/13/111721083.gif) 的最小值即可。
的最小值即可。如何统计答案:
先遍历所有子树,从
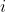 到
到  记录
记录 ![w[i]-d[i]](https://1000bd.com/contentImg/2022/08/13/111722192.gif) 表示从
表示从 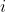 到
到  的剩余油量。
的剩余油量。从
 到
到 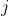 记录
记录 ![w[fa[j]]-d[j]](https://1000bd.com/contentImg/2022/08/13/111723324.gif) 的最小值。
的最小值。将两种情况按升序排序,用双指针来维护答案的区间。
答案区间为
![w[k]-d[k]+w[f[a[j]]-d[j]](https://1000bd.com/contentImg/2022/08/13/111724115.gif) 的
的 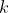 都可以。
都可以。注意,像上面所说,要先把
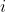 和
和 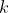 在同一棵子树中的情况提前删掉。
在同一棵子树中的情况提前删掉。 总代码:
- #include
- #include
- #include
- #include
- #include
- #define re register
- #define int long long
- #define drep(a,b,c) for(re int a(b) ; a>=(c) ; --a)
- #define rep(a,b,c) for(re int a(b) ; a<=(c) ; ++a)
- using namespace std;
- inline int read(){
- int x=0,f=1;char ch=getchar();
- while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
- while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
- return x*f;
- }
- const int M = 2e5+10;
- int n;
- int head[M],siz[M],maxp[M],vis[M],a[M];
- int w[M],d[M],tmp1[M],tmp2[M],q1[M],q2[M];
- int root,sum,ans,cnt,cnt1,cnt2;
- struct edge{
- int to,nxt,w;
- }e[M];
- inline void add(int u,int v,int w){ //村边
- e[++cnt].to = v;
- e[cnt].w = w;
- e[cnt].nxt = head[u];
- head[u] = cnt;
- }
- inline void getroot(int u,int fa){
- siz[u] = 1;maxp[u] = 0; //maxp记录该节点的最大的子树的size
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(vis[v] || v==fa) continue;
- getroot(v,u);
- siz[u] += siz[v];
- maxp[u] = max(maxp[u],siz[v]); //找最大
- }
- maxp[u] = max(maxp[u],sum-siz[u]); //注意,该节点外部也可能有点,要考虑到
- if(maxp[u] < maxp[root]) root = u; //更新重心
- }
- inline void dfs(int u,int fa,int mx,int mi){
- if(w[u] - d[u] >= mx) tmp1[++cnt1] = w[u]-d[u]; //把符合要求的记录下来
- tmp2[++cnt2] = mi; //因为不确定从root到j的路径是从哪一个点开始,所以也都要记录下来
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(v==fa || vis[v]) continue;
- d[v] = d[u]+e[i].w; //更新边权之和
- w[v] = w[u]+a[v]; //更新点权之和
- dfs(v,u,max(mx,w[u]-d[u]),min(mi,w[u]-d[v])); //往下接着更新
- }
- }
- inline void solve(int u){
- int tot1=0,tot2=0;
- d[u] = 0,w[u] = a[u]; //初始化
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(vis[v]) continue;
- cnt1 = cnt2 = 0;
- d[v] = e[i].w,w[v] = w[u]+a[v]; //初始化两个数组
- dfs(v,u,w[u]-d[u],w[u]-d[v]); //进行dfs,找tmp1和tmp2来更新答案
- sort(tmp1+1,tmp1+cnt1+1); //升序
- sort(tmp2+1,tmp2+cnt2+1); //tmp1和tmp2记录的是当前子树内的路径
- int l = 1;
- for(re int i(cnt2) ; i>=1 ; --i){ //注意是反着枚举,相当于双指针维护
- while(l<=cnt1 && tmp1[l]+tmp2[i]-a[u]<0) l++; //如果改路径不符合要求
- ans -= cnt1-l+1; //把在同一棵子树内的贡献给删掉
- }
- for(re int i(1) ; i<=cnt1 ; ++i) q1[++tot1] = tmp1[i];
- for(re int i(1) ; i<=cnt2 ; ++i) q2[++tot2] = tmp2[i]; //q1和q2记录的是所有的路径
- }
- sort(q1+1,q1+tot1+1); //同样升序排序
- sort(q2+1,q2+tot2+1);
- int l = 1;
- for(re int i(tot2) ; i>=1 ; --i){ //双指针找答案
- if(q2[i] >= 0) ans++; //相当于可以直接从root出发到j,那么直接+1即可
- while(l<=tot1 && q1[l]+q2[i]-a[u]<0) l++; //从i到root和从root到j加了两次a[root],减去就行
- ans += tot1-l+1; //更新答案
- }
- ans += tot1; //这是加上从i出发直接到root结束的情况
- }
- inline void work(int u){
- vis[u] = 1; //相当于把这个点删了
- solve(u); //从这个点开始
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(vis[v]) continue;
- maxp[root = 0] = sum = siz[v]; //重新找重心
- getroot(v,0);
- getroot(root,0); //注意还是两次
- work(root); //重复该过程
- }
- }
- signed main(){
- n=read();
- rep(i,1,n) a[i] = read();
- rep(i,1,n-1){
- int u=read(),v=read(),w=read();
- add(u,v,w),add(v,u,w);
- }
- maxp[0] = sum = n; //注意要先赋值
- getroot(1,0);
- getroot(root,0); //可以算是一个细节吧,因为如果只找一次根,
- //那么记录的siz数组很有可能不是以root为根的size
- work(root); //从root开始点分治
- printf("%lld\n",ans);
- return 0;
- }
-
相关阅读:
centos jenkins 无法启动 active (exited)
Spring In Action 5 学习笔记 chapter1 拓展
蓝桥算法赛(摆玩具)
每日一题~组合总数III
python多线程是如何工作
select条目对象
Java中String对象的replaceAll方法调用性能优化小技巧
八股文随笔1
Spring项目bean 无法注入问题--Thread中注入Bean无效-多线程下@Resource和@Autowired和@Value 注入为null
第一百五十一回 自定义组件综合实例:游戏摇杆二
- 原文地址:https://blog.csdn.net/glorious_dream/article/details/126254904
