---

一、KMP(单模式)

KMP算法是一种改进的字符串匹配算法,其算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next() 函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)

图解：

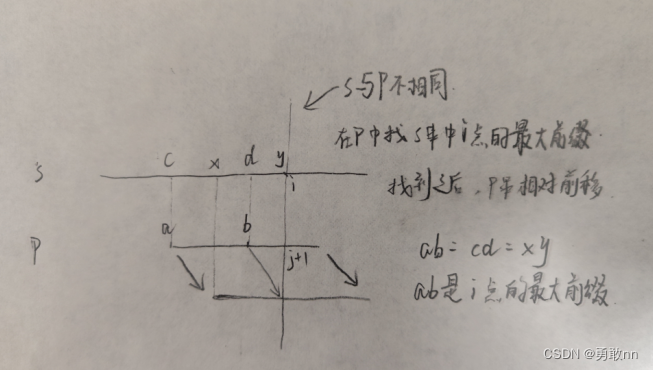
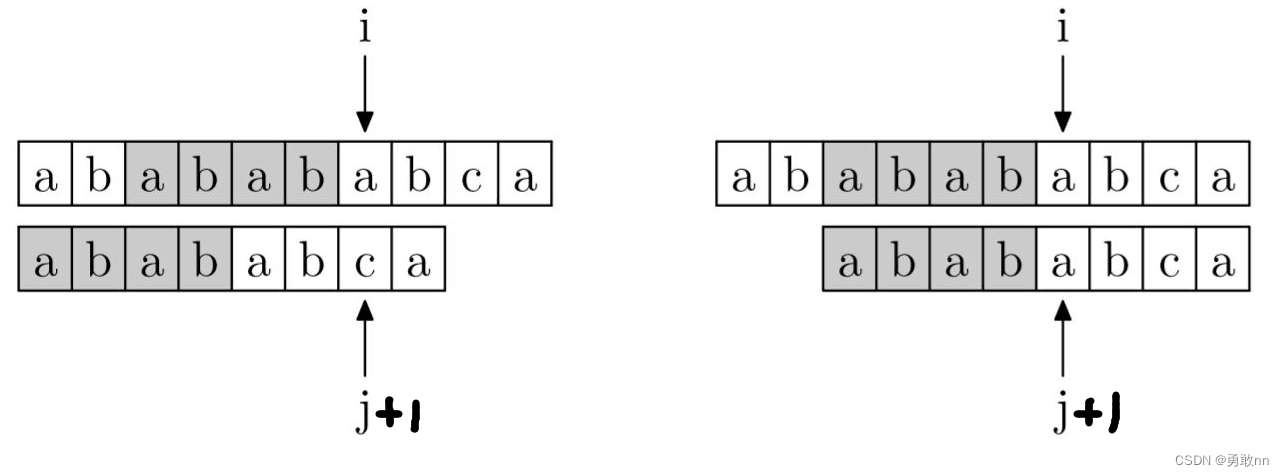
输入：
3
aba
5
ababa
输出：
0 2
1
2
3
4
5
6
7

#include
using namespace std;

int n,m;
int ne[100010];
char p[100010],s[1000010];

int main()
{
    cin>>n>>p+1>>m>>s+1;
    //初始化next数组
    for(int i=2,j=0;i<=n;i++)
    {
        while(j&&p[i]!=p[j+1]) j=ne[j]; //j!=0防止进入死循环，如果当前位置(j+1)与模板的位置i不匹配，就向前找 当前位置前一个位置(j)的最大前缀的尾部，然后继续比较下一个位置
        if(p[i]==p[j+1]) j++;
        ne[i]=j;
    }
    //kmp匹配过程
    for(int i=1,j=0;i<=m;i++)
    {
        while(j&&s[i]!=p[j+1]) j=ne[j];
        if(s[i]==p[j+1]) j++;
        if(j==n) //匹配成功
        {
            printf("%d ",i-n);
            j=ne[j];
        }
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

二、Trie(字典树，多模式)

Trie是一种高效地存储和查找字符串集合地数据结构，又称单词查找树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

1. Trie字符串统计

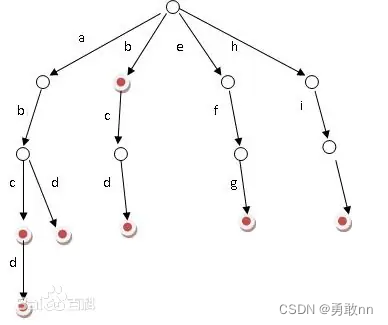
输入：
5
I abc
Q abc
Q ab
I ab
Q ab
输出：
1
0
1
1
2
3
4
5
6
7
8
9
10
11

代码如下:

#include
using namespace std;

const int N=100010;
int son[N][26],cnt[N],idx; //cnt存每一个单词地个数
char str[N];
void insert(char str[])
{
    int p=0; //根节点地idx为0，根节点不存储字母
    for(int i=0; str[i]; i++)
    {
        int u=str[i]-'a';
        if(!son[p][u]) son[p][u]=++idx; //每一个节点都有一个单独的idx
        p=son[p][u];//存下一个节点的编号
    }
    cnt[p]++;
}
int query(char str[])
{
    int p=0;
    for(int i=0; str[i]; i++)
    {
        int u=str[i]-'a';
        if(!son[p][u]) return 0;
        p=son[p][u];
    }
    return cnt[p];
}
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        char op[2];
        scanf("%s %s",op,str);
        if(op[0]=='I') insert(str);
        else printf("%d\n",query(str));
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

2. 最大异或对

题目描述：
在给定的 N 个整数 A1，A2……AN 中选出两个进行异或运算，得到的结果最大是多少？

输入：
3
1 2 3
输出：
3
1
2
3
4
5

#include 
#include 
using namespace std;

const int N = 100010, M = 3100010;
int n;
int a[N], son[M][2], idx;

void insert(int x)
{
    int p = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int &s = son[p][x >> i & 1];//x的第i+1位
        if (!s) s = ++ idx;//建立一个新结点
        p = s;
    }
}

int search(int x)
{
    int p = 0, res = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int s = x >> i & 1;
        if (son[p][!s])//存在相反位
        {
            res += 1 << i;
            p = son[p][!s];
        }
        else p = son[p][s];//不存在相反位
    }
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        scanf("%d", &a[i]);
        insert(a[i]);
    }
    int res = 0;
    for (int i = 0; i < n; i ++ ) res = max(res, search(a[i]));
    printf("%d\n", res);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

三、AC自动机(多模式)

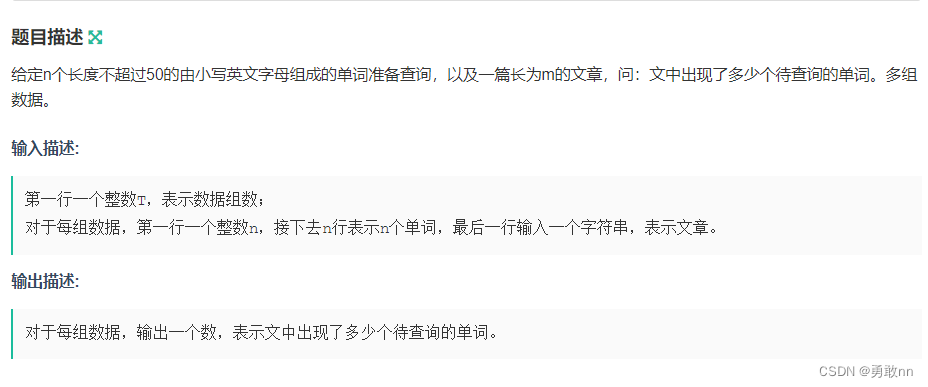
输入：1
5
she
he
say
shr
her
yasherhs
输出：
3
1
2
3
4
5
6
7
8
9
10

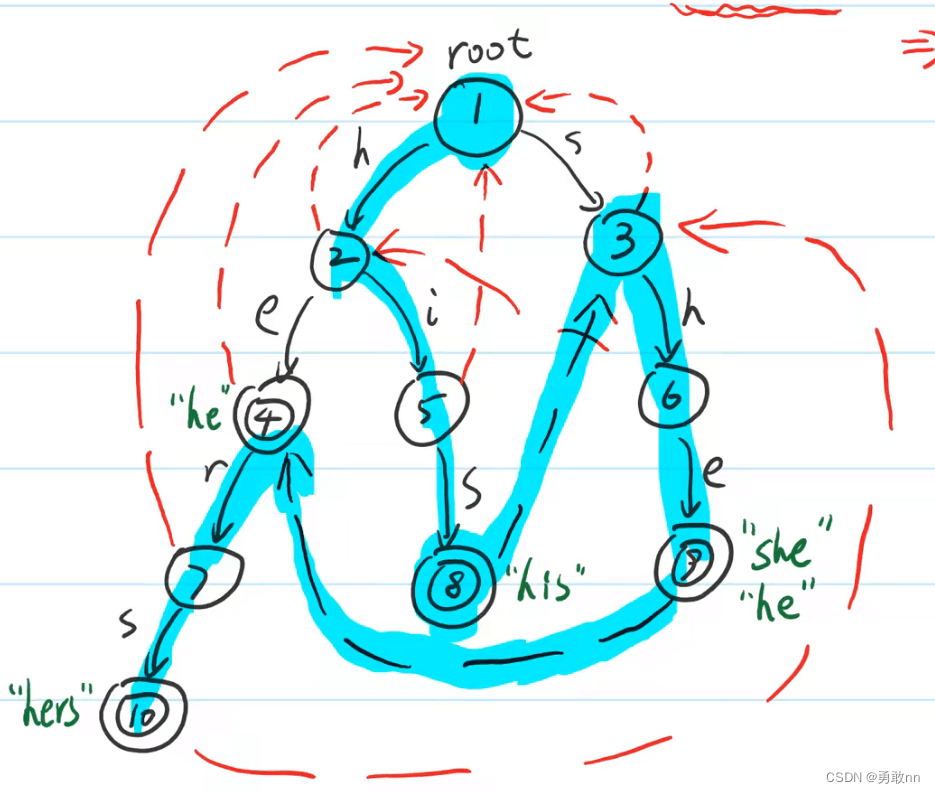
#include
#include
#include
#include
using namespace std;

typedef long long ll;
ll n,idx=1;
ll trie[500050][26];
ll cnt[500050]; //cnt存单词的尾部，统计该单词出现的次数
ll ne[500050]; //next数组找到其最大后缀所在的位置
ll ans;

void INSERT(string s)
{
    ll root=1;
    for(int i=0; i<s.size(); i++)
    {
        int id=s[i]-'a';
        if(!trie[root][id]) trie[root][id]=++idx;
        root=trie[root][id];
    }
    cnt[root]++;
}

void bfs_next()
{
    queue<ll> q;
    for(int i=0;i<26;i++)
    {
        trie[0][i]=1;
    }
    q.push(1); //将根节点放入队列
    ne[1]=0;
    while(q.size())
    {
        int u=q.front();
        q.pop();
        for(int i=0;i<26;i++)
        {
            if(!trie[u][i]) trie[u][i]=trie[ne[u]][i]; //剪枝
            else
            {
                q.push(trie[u][i]);
                int v=ne[u];
                ne[trie[u][i]]=trie[v][i]; //儿子指向父节点next数组指向的位置的子节点，如果该节点不存在，则指向root
            }
        }
    }
}

void FIND(string s)
{
    int root=1;
    for(int i=0;i<s.size();i++)
    {
        int id=s[i]-'a';
        int k=trie[root][id];
        while(k>1) //从当前节点开始，递归遍历完每个节点对应的最长后缀，直到后缀长度为0，即回到root
        {
            ans+=cnt[k];
            cnt[k]=0;
            k=ne[k];
        }
        root=trie[root][id]; //儿子变成父亲
    }
}

int main()
{
    ios::sync_with_stdio(false); //此时只能用cin，而不能用scanf
    int t;
    cin>>t;
    while(t--)
    {
        ans=0;
        memset(cnt,0,sizeof cnt);
        memset(trie,0,sizeof trie);
        memset(ne,0,sizeof ne);
        cin>>n;
        string s;
        for(int i=1; i<=n; i++)
        {
            cin>>s;
            INSERT(s);
        }
        bfs_next();
        cin>>s;
        FIND(s);
        cout<<ans<<endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93