-
矩阵分析与应用(21)
学习来源:《矩阵分析与应用》 张贤达 清华大学出版社
奇异值分解
1. 特征值分解(EVD)
对于一个对称矩阵来说,它能相似对角化,且对称矩阵的不同特征值对应的特征向量两两正交。设矩阵
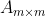 为满秩对称矩阵,有
为满秩对称矩阵,有 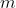 个不同的特征值,为
个不同的特征值,为  ,特征值对应的特征向量为
,特征值对应的特征向量为  ,则
,则

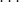

所以有

其中,
![U=[x_1,x_2,\cdots ,x_m]](https://1000bd.com/contentImg/2022/08/12/193641621.gif)

由于
 为对称矩阵,所以
为对称矩阵,所以  的特征向量两两正交,即
的特征向量两两正交,即 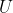 为正交矩阵,因此
为正交矩阵,因此 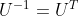 。
。所以可以得到矩阵
 的特征值分解:
的特征值分解:
2. 奇异值分解
回顾一下矩阵奇异值分解的定义:
设
 ,则存在
,则存在 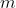 阶正交矩阵
阶正交矩阵 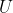 和
和 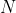 阶正交矩阵
阶正交矩阵  使得
使得
其中,
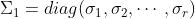 ,而
,而  为
为  的非零奇异值。
的非零奇异值。1)
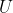 矩阵求解
矩阵求解由
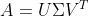 ,
,  可得
可得  。
。因为
 是一个
是一个 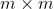 方阵,可以进行特征值分解,因此
方阵,可以进行特征值分解,因此  ,
,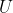 由
由  的特征值对应的特征向量组成。
的特征值对应的特征向量组成。2)
 矩阵求解
矩阵求解由
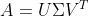 ,
,  可得
可得  。
。 是
是 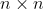 方阵,可由特征值分解知道
方阵,可由特征值分解知道  由
由  的特征值对应的特征向量组成。
的特征值对应的特征向量组成。3. 例
求解矩阵
 的奇异值分解。
的奇异值分解。1)

特征值为
 。
。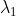 对应的特征向量为
对应的特征向量为 ![x_1=[\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}]^T](https://1000bd.com/contentImg/2022/08/12/193712529.gif) ,
,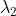 对应的特征向量为
对应的特征向量为 ![x_2=[\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0]^T](https://1000bd.com/contentImg/2022/08/12/193715193.gif)
因此
 ,且
,且  。
。2)

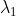 对应的特征向量为
对应的特征向量为 ![y_1=[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T](https://1000bd.com/contentImg/2022/08/12/193719153.gif) ,
,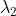 对应的特征向量为
对应的特征向量为 ![y_2=[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T](https://1000bd.com/contentImg/2022/08/12/193720598.gif)
因此
 。
。3)矩阵
 的奇异值分解为
的奇异值分解为 -
相关阅读:
笔记本电脑没有声音?几招恢复声音流畅!
Python简单实现人脸识别检测, 对照片进行评分
《014.SpringBoot+vue之学生选课管理系统03》【前后端分离】
【软考 系统架构设计师】计算机组成与体系结构⑥ 流水线
Root of AVL Tree (25)
5 | Java Spark WordCount打成Jar 包测试
【数值计算】基于四阶Runge-Kutta方法实现Mackey_Glass混沌时间序列生成以及相位时差的绘制附matlab代码
使用Node.js手撸一个建静态Web服务器,内部CV指南
24节气查询易语言代码
K8S环境搭建
- 原文地址:https://blog.csdn.net/qq_40206924/article/details/126233861