leetcode

递归函数何时需要返回值

递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

1. 如果需要搜索整棵二叉树
   • 如果不用处理递归返回值，递归函数就不要返回值。（113.路径总和ii：找到所有等于targetsum的路径）
   • 如果需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）
2. 如果要搜索其中一条符合条件的路径
   • 需要返回值，因为遇到符合条件的路径了就要及时返回。（112 路径总和，找到一条等于targetsum的路径。True/False）

1 二叉树的四种遍历

关于二叉树的定义和前中后序，层序遍历。

https://blog.csdn.net/weixin_42327752/article/details/124019951

LC题目：

• 144.二叉树的前序遍历(opens new window)
• 145.二叉树的后序遍历(opens new window)
• 94.二叉树的中序遍历
• 102.二叉树的层序遍历
• 107.二叉树的层次遍历II

2 二叉树的高度/深度

104.二叉树深度

题目：计算最大深度

核心思路：

使用dfs，前/后序遍历，记录左右子树的此时深度，返回max（l,r）
因为，需要一个变量保存深度值，所以在dfs中必须有返回值。

代码：

class Solution:
    def getdepth(self,root):
            if not root :
                return 0
            ldep = self.getdepth(root.left)
            rdep = self.getdepth(root.right)
            dep = 1 + max(ldep, rdep)
            return dep
            
    def maxDepth(self, root: Optional[TreeNode]) -> int: 
        return self.getdepth(root)
1
2
3
4
5
6
7
8
9
10
11

其中，也可以这样(前序遍历)：

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        dep = 0
        def dfs(root,dep):
            if not root:
                return dep
            ldep = dfs(root.left,dep + 1)
            rdep = dfs(root.right,dep + 1)
            return max(ldep,rdep)
        return dfs(root,dep)
1
2
3
4
5
6
7
8
9
10

111.二叉树的最小深度

和最大深度一样，return min(ldep,rdep)

222.完全二叉树的节点个数

题目：计算二叉树的节点个数

核心思路：

和上面计算深度一样的思路，采用后序遍历，返回左子树节点数+右子树节点数。

代码：

        def dfs (root):
            if not root:
                return 0
            lnums = dfs(root.left)  # 左
            rnums = dfs(root.right)  # 右
            nums = lnums + rnums + 1  # 前
            return nums
1
2
3
4
5
6
7

110.平衡二叉树

题目：高度平衡二叉树：左右子树高度差不大于1。

核心思路：

1 先计算当前节点的高度
2 在判断左右节点的高度差<=1 and 左子树高度平衡 and 右子树高度平衡

代码：

return abs(dfs(root.left)-dfs(root.right))<=1 and self.isBalanced(root.left) and self.isBalanced(root.right)
1

3 二叉树的翻转和对称

226.翻转二叉树

题目：
按中心轴翻转二叉树

核心思路：

实现二叉树的翻转，也就是对左右节点进行互换。

代码：
前序遍历写法,这里不可以用中序遍历，在左中右时，左右分别进行了一次交换。

def dfs(root):
    if not root:
        return 
    root.left, root.right = root.right, root.left
    dfs(root.left)
    dfs(root.right)
1
2
3
4
5
6

101. 对称二叉树

100. 相同的数

题目:判断是否对称

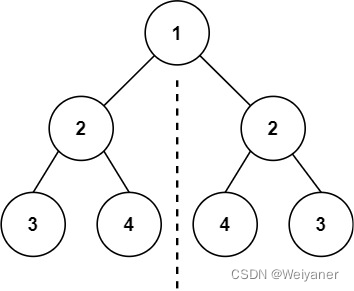
核心思路：

对于根节点的左右两个子树，左节点——右节点，右节点——子节点判断是否一样。不一样就返回False.
需要注意的是，只有在左右节点都是空的情况下才可以返回True，不能比较一次结点一样就返回True。

代码：

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if not root: 
            return False
        def dfs(root1, root2):
            if root1 and not root2:
                return False
            elif not root1 and root2: 
                return False
            elif not root2 and not root1:
                return True
            elif root1.val != root2.val:
                return False
            # else:  #不可以加else,因为还需要继续向下一层进行比较，只有都是空才可以返回True
            #     return True
            return dfs(root1.left, root2.right) and dfs(root1.right, root2.left)
        return dfs(root.left, root.right)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

4 二叉树的路径

4.1 引言

涉及到路径的，都需要回溯，所以本章节就是结合了前中后序遍历的递归+回溯。

257. 二叉树的所有路径

题目：
返回所有路径

核心思路：

进行遍历和回溯
当遇到叶子节点，将这条路径的值path保存到res。所以终止条件是：if not root.left and not root.right:
在进行中左右的左右节点遍历

代码：

        def dfs(root,path):
            path += str(root.val)
            if not root.left and not root.right:
                res.append(path)
                # return 
            if root.left:
                dfs(root.left, path + '->')  # 将path写进dfs里面，就不用写出显式回溯了
            if root.right:
                dfs(root.right, path + '->')
1
2
3
4
5
6
7
8
9

112. 路径总和

题目：存在路径和为targetsum，返回True

思路：

方法1：找到所有路径，判断。由于是遍历整棵树，无需返回值，直接保存路径到res。

所有路径：

        def dfs(root,path):
            path.append(root.val)  # 中
            if not root.left and not root.right:
                res.append(path[:])
            if root.left:  # 左
                dfs(root.left, path)
            if root.right:  # 右
                dfs(root.right, path)
            path.pop()  # 回溯
1
2
3
4
5
6
7
8
9

方法2： 直接判断。遇到就返回True，否则返回False。所以需要返回值。最后返回l or r。

class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        target,res = targetSum, []
        def dfs(root,target):
            if not root:
                return False
            if target==root.val and not root.left and not root.right:
                return True
            l = dfs(root.left,target-root.val)
            r = dfs(root.right,target-root.val)
            return l or r
        return dfs(root,target)
1
2
3
4
5
6
7
8
9
10
11
12

113. 路径总和 II

找到所有路径和=targetsum的路径

思路：

搜索整棵树，且无需操作返回值，因此无需返回值。

代码：

def dfs(root,targetSum,path):
    path.append(root.val)
    if not root.left and not root.right and root.val == targetSum:
        res.append(path[:])
    if root.left:
        dfs(root.left, targetSum-root.val, path)
    if root.right:
        dfs(root.right, targetSum-root.val, path)
    path.pop()
1
2
3
4
5
6
7
8
9

404.左叶子之和

题目： 计算所有左叶子节点的和

核心思路：

终止条件：左叶子节点 if root.left and not root.left.left and not root.left.right:

代码：

class Solution:
    def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
        res = []
        def dfs(root):
            if root.left and not root.left.left and not root.left.right:
                res.append(root.left.val)
            if root.left:
                dfs(root.left)
            if root.right:
                dfs(root.right)
        dfs(root)
        return sum(res)
1
2
3
4
5
6
7
8
9
10
11
12

513. 找树左下角的值

题目： 最后一行最左侧的值

思路：

方法1：层序遍历，最后一行第一个即可
方法2：dfs，找到最后一一行的第一个值，需要结合计算深度

5 构造二叉树

5.1 前中后二者确定二叉树

前+中可以确定一棵二叉树
后+中也可以确定一棵二叉树
qian+hou不可以确定。因为没有中序遍历来进行划分左右子树区间。

106. 从中序与后序遍历序列构造二叉树

思路：

1 取出后序遍历的最后一个值
2 作为中序遍历的分节点，划分左右两个子区间，进行递归，即可。
3 注意实现的过程中，由于要对postorder进行pop，所以长度会变小，在递归中，也需要inorder进行长度裁切。
4 另外，位置对应关系：node.right = dfs(postorder[idx:],inorder[idx+1:])

代码：

        def dfs(postorder,inorder):
            if not postorder:
                return 
            val = postorder.pop()
            idx = inorder.index(val)
            node = TreeNode(val)
            node.left = dfs(postorder[:idx],inorder[:idx])
            node.right = dfs(postorder[idx:],inorder[idx+1:])
            return node
1
2
3
4
5
6
7
8
9

105.从前序与中序遍历序列构造二叉树

改动：val = postorder.pop(0)

5.2

654. 最大二叉树

题目：
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。

思路：

和上面中序遍历划分子树类似。

模板：

        def dfs(nums):
            if not nums:
                return
            val = max(nums)
            idx = nums.index(val)
            node = TreeNode(val)
            node.left = dfs(nums[:idx])
            node.right = dfs(nums[idx+1:])
            return node
1
2
3
4
5
6
7
8
9

617. 合并二叉树

题目：相同节点值合并，得到新的二叉树

思路：

使用其中一个二叉树进行原地修改
三种遍序都是都可以
终止条件：其中一个空，return 另一个节点

代码：

        def dfs(root1, root2):
            if not root2:
                return root1
            if not root1:
                return root2
            root1.val += root2.val
            root1.left = dfs(root1.left, root2.left)
            root1.right = dfs(root1.right, root2.right)
            return root1
1
2
3
4
5
6
7
8
9

701.二叉搜索树中的插入操作

108. 将有序数组转换为二叉搜索树

题目：构造出高度平衡的二叉搜索树。高度平衡：左右子树的高度差不超过1

分析：

这和上面的654最大二叉树没有什么区别，在本题中，对于升序数组，考虑高度平衡，每次需要从数组中间划分，作为左右子树。(654是从最大值划分。)

代码：

        def dfs(nums):
            if not nums:
                return
            idx = len(nums)//2
            node = TreeNode(nums[idx])
            node.left = dfs(nums[:idx])
            node.right = dfs(nums[idx+1:])
            return node
1
2
3
4
5
6
7
8

6 二叉搜索树

二叉搜索树性质

二叉搜索树是一种有序二叉树，左节点<根节点<右节点

根据此，进行中序遍历就可以得到一个升序的list。

700.二叉搜索树中的搜索

题目：找到节点值为target的子树

思路：

普通二叉树就是直接前中后序遍历即可
二叉搜索树利用性质，进行单侧搜索。遇到就返回节点

代码：

        def dfs(root):
            if not root:
                return 
            if root.val > val:
                return dfs(root.left)
            elif root.val < val:
                return dfs(root.right)
            else:
                return root
1
2
3
4
5
6
7
8
9

98. 验证二叉搜索树

思路：中序遍历，看是否升序。

530. 二叉搜索树的最小绝对差

701.二叉搜索树中的插入操作

题目：
给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

思路：

最简单的插入方式，中序遍历，找到空节点，然后按大小看放左边还是右边。

代码：

        def dfs(root):
            if not root:
                root = TreeNode(val)
                return root
            if root.val > val:
                root.left = dfs(root.left)
            if root.val < val:
                root.right = dfs(root.right)
            return root
1
2
3
4
5
6
7
8
9

450.删除二叉搜索树中的节点

669. 修剪二叉搜索树

题目：只保留区间内的节点。返回一颗新二叉树。
代码：

        def dfs(root):
            # 终止条件
            if not root:
                return
            ## 异常点操作
            if root.val < low:
                return dfs(root.right)
            if root.val > high:
                return dfs(root.left)
            # 正常点操作
            root.left = dfs(root.left)
            root.right = dfs(root.right)
            return root
1
2
3
4
5
6
7
8
9
10
11
12
13

538. 把二叉搜索树转换为累加树

---

7 公共祖先

236. 二叉树的最近公共祖先

题目：
两个指定节点的最近公共祖先

思路：

使用后序遍历，从低向上，那么第一个公共祖先就是最近的。
遍历全棵树，当时需要对返回值操作，因此需要返回值。
终止条件：两个节点分别在左右子树。

代码：

        def dfs(root):
            if root == p or root == q:
                return root
            if not root:
                return
            l = dfs(root.left)
            r = dfs(root.right)
            if l and r:
                return root
            elif l:
                return l
            else:
                return r
1
2
3
4
5
6
7
8
9
10
11
12
13

235. 二叉搜索树的最近公共祖先

利用二叉搜索树性质，最近的公共祖先必然位于p，q区间.

        def dfs(root):
            if not root:
                return
            if root.val > p.val and root.val > q.val:
                return dfs(root.left)
            elif root.val < p.val and root.val < q.val:
                return dfs(root.right)
            else:
                return root
1
2
3
4
5
6
7
8
9

总结

代码随想录二叉树总结