欧拉角

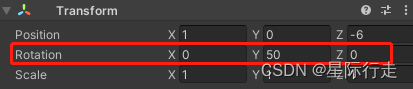
使用三个角度来保存方位，如（0, 50, 0）。

X和Z沿自身坐标系旋转，Y沿世界坐标系旋转。

获取物体欧拉角：Vector3 eulerAngle = transform.eulerAngles;

优点：

1、仅使用三个数字保存方位，占用空间小。

2、沿坐标轴旋转的单位为角度，符合人的思考方式。

3、任意三个数字都是合法的，不存在不合法的欧拉角。

缺点：

一、方位的表达方式不唯一。

1、对于一个方位，存在多个欧拉角描述，因此无法判断多个欧拉角代表的角位移是否相同。

例如：

-- 角度0,5,0与角度0,365,0

-- 角度0,-5,0与角度0,355,0

-- 角度250,0,0与角度290,180,180

前面两种还好，第三种就比较复杂了。

2、为了保证方位表达方式唯一，unity限制了角度范围，即沿X轴旋转限制在-90到90之间，沿Y与Z旋转限制在-180到180之间。（实测，代码中修改欧拉角会受这个限制，之间在场景中修改欧拉角不受该限制）

这里就有个问题，如果修改欧拉角的x值，想让物体一直旋转，但是达到限制角度后，物体就不会继续旋转了。

二、万向节死锁

物体沿X轴旋转±90度，自身坐标系Z轴与世界坐标系Y轴将会重合，此时再沿Y轴或Z轴旋转时，将失去一个自由度。

在万向节死锁情况下，规定沿Z轴完成绕竖直轴的旋转，即此时Y轴旋转为0。

四元数

四元数Quaternion在3D图形学中代表旋转，由一个三维向量（x/y/z）和一个标量（w）组成。

旋转轴为V，旋转弧度为θ，如果使用四元数表示，则四个分量为：

x=sin(θ/2)*V.x

y=sin(θ/2)*V.y

z=sin(θ/2)*V.z

w=cos(θ/2)

x、y、z、w的取值范围是-1到1.

Quaternion qt = transform.rotation;
transform.rotation = Quaternion.Euler(0, 50, 0);

优点：避免万向节死锁

缺点：

1、难于使用，不建议单独修改某个数值。

2、存在不合法的四元数。

与向量相乘

四元数左乘向量，表示将该向量按四元数表示的角度旋转。

Vector3 newVec3 = Quaternion.Euler(0, 30, 0) * new Vector3(0, 0, 10);

如计算物体右前方30度，10m远坐标。

Vector3 vec3 = transform.rotation * new Vector3(0, 0, 10);
vec3 = Quaternion.Euler(0, 30, 0) * vec3;
vec3 = transform.position + vec3;

与四元数相乘

两个四元数相乘可以组合旋转效果

Quaternion q1 = Quaternion.Euler(0, 20, 0) * Quaternion.Euler(0, 30, 0);
Quaternion q2 = Quaternion.Euler(0, 50, 0);
// q1和q2相同
 
transform.rotation *= Quaternion.Euler(0, 1, 0);    // 沿自身y轴旋转
transform.Rotate(0, 1, 0);  // 内部就是使用四元数相乘实现

四元数实战：炸弹-障碍物-玩家范围判定

问题如下图：

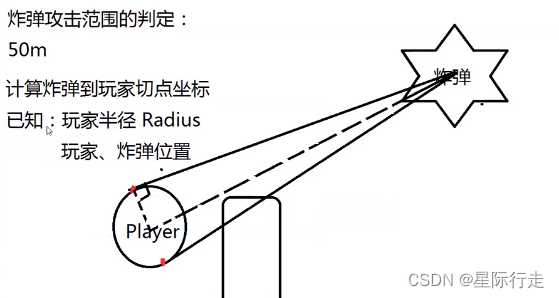
这里只讨论求出两个切点。思路见下图：

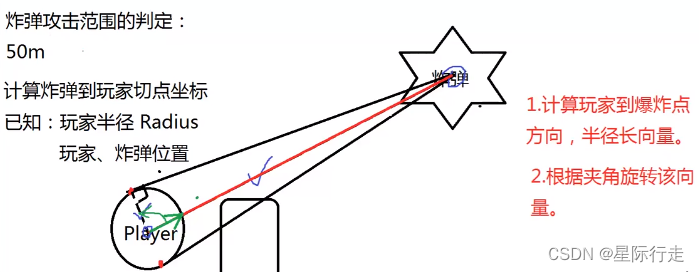
计算出两个切点坐标后，计算两切线是否与障碍物相交，即可判定玩家是否被炸伤。

代码如下：

public Transform tranPlayer;
private float playRadius = 0.5f;
 
public Vector3 leftTangetPoint; // 左切点
public Vector3 rightTangetPoint; // 右切点
 
// 计算切点
void CalculateTangent()
{
    Vector3 playerPos = tranPlayer.position;
    Vector3 playerToBomb = transform.position - playerPos;
    Vector3 playerToBombRadius = playerToBomb.normalized * playRadius;  // 半径向量
    float angles = Mathf.Acos(playRadius / playerToBomb.magnitude) * Mathf.Rad2Deg;
 
    leftTangetPoint = playerPos + Quaternion.Euler(0, angles, 0) * playerToBombRadius;  // 用四元数旋转半径向量
    rightTangetPoint = playerPos + Quaternion.Euler(0, -angles, 0) * playerToBombRadius;
}
 
void Update()
{
    CalculateTangent();
    Debug.DrawLine(transform.position, leftTangetPoint);
    Debug.DrawLine(transform.position, rightTangetPoint);
}

四元数API的应用示例

public Transform tf;
//1、欧拉角转四元数
Quaternion.Euler(0, 50, 0);
 
//2、四元数转欧拉角
Quaternion qt = transform.rotation;
Vector3 euler = qt.eulerAngles;
 
//3、沿任意轴旋转角度，参数2可以传任意向量作为轴
transform.rotation = Quaternion.AngleAxis(50, Vector3.up);
 
//4、z轴指向一个方向, transform的z轴指向tf所在位置
Vector3 dir = tf.position - transform.position; // 方向向量
transform.rotation = Quaternion.LookRotation(dir);  // 根据方向向量，求出对应的四元数
 
 
// 按给定速度旋转
Quaternion qTarget = Quaternion.LookRotation(tf.position - transform.position);
//5、匀速旋转，z轴指向目标
transform.rotation = Quaternion.RotateTowards(transform.rotation, qTarget, 0.05f);
//6、插值旋转，z轴指向目标
transform.rotation = Quaternion.Lerp(transform.rotation, qTarget, 0.01f);
//7、求两四元数的夹角
if (Quaternion.Angle(qTarget, transform.rotation) < 1)
{
    transform.rotation = qTarget;
}
 
 
//X轴注视旋转
//8、x轴注视旋转， transform.right可以get和set
transform.right = tf.position - transform.position;
//9、x轴注视旋转。创建四元数，从开始方向旋转到目标方向
transform.rotation = Quaternion.FromToRotation(transform.right, tf.position - transform.position);