线性规划（一）——概念

研究的问题

• 在一项任务目标确定后，如何以最低的成本（经费、人力、物资等）实现该目标
  • 例如：某汽车工厂今年要完成N辆汽车的生产，汽车生产需要消耗人力、物资材料等。如何尽可能地用最少的人力成本、材料成本完成N辆汽车的生产？
  • 例如：某购物商场每日顾客人数不同，需要的销售人员数量不同。如何在满足顾客需求的情况下，对销售人员排班，以尽可能的降低雇佣的销售人员的数量？
• 在现有的资源条件下，如何进行组织、安排，以实现最大化的收益
  • 例如：某汽车工厂现有A、B、C原料固定数量，生产不同车型需要的原料不同，收益也不同。如何在已有的原材料的情况下，尽可能多的提高收益？
  • 例如：某设计院现有N位设计师，设计不同等级的图花费的人力成本不同、盈利不同。如何在有限数量的设计师情况下，安排设计工作，以实现更多的盈利？

例子——汽车工厂的生产、盈利（图解法）

• 描述
  • 某汽车工厂生产A、B两种车型，这两种车生产一辆分别需要不同的甲、乙原材料。
  • 生产一辆A车，需要2.5吨甲材料、2吨乙材料，能盈利12万元。
  • 生产一辆B车，需要1吨甲材料、1.5吨乙材料，能盈利7万元。
  • 甲材料的供给上限为50吨、乙材料的供给上限为60吨。
  • 列出图表如下

• 问题
  • 该汽车工厂应该如何规划A、B汽车的生产数量以达到最大的收益？
• 分五个步骤解决问题
  1. 我们的目的是：确定使得利益最大化时，A、B汽车的数据量各是多少。
  2. 设生产A车共$x_1$辆，生产B车共$x_2$辆，则收益目标函数为
     $$f(x)=12x_1+7x_2$$
  3. 因为甲、乙材料有数量限制，A、B汽车数据应为非负，显然
     { 2.5 x 1 + x 2 ≤ 50 2 x 1 + 1.5 x 2 ≤ 60 x 1 ≥ 0 , x 2 ≥ 0
     {2.5x1+x2≤502x1+1.5x2≤60x1≥0,x2≥0" role="presentation" style="position: relative;">⎧⎩⎨2.5x1+x2≤502x1+1.5x2≤60x1≥0,x2≥0$$\{\begin{array}{l}2.5x_1+x_2\le 50\\ 2x_1+1.5x_2\le 60\\ x_1\ge 0,x_2\ge 0\end{array}$$
     ⎩ ⎨ ⎧​2.5x1​+x2​≤502x1​+1.5x2​≤60x1​≥0,x2​≥0​
  4. 由此，可得到数学模型
     max ⁡ { f = 12 x 1 + 7 x 2 } s.t. 2.5 x 1 + x 2 ≤ 50 2 x 1 + 1.5 x 2 ≤ 60 x j ≥ 0 , j = 1 , 2
     max{f=12x1+7x2}s.t.2.5x1+x2≤502x1+1.5x2≤60xj≥0,j=1,2" role="presentation" style="position: relative;">maxs.t.{f=12x1+7x2}2.5x1+x2≤502x1+1.5x2≤60xj≥0,j=1,2$$\begin{array}{ll}max& \left\{f=12x_1+7x_2\right\}\\ \text{s.t.}& 2.5x_1+x_2\le 50\\ & 2x_1+1.5x_2\le 60\\ & x_j\ge 0,j=1,2\end{array}$$
     maxs.t.​{f=12x1​+7x2​}2.5x1​+x2​≤502x1​+1.5x2​≤60xj​≥0,j=1,2​
  5. 求解
     1. 目前问题较为简单，可采用图解法
     2. 以$x_1$作为横轴、$x_2$作为纵轴，作图如下
        
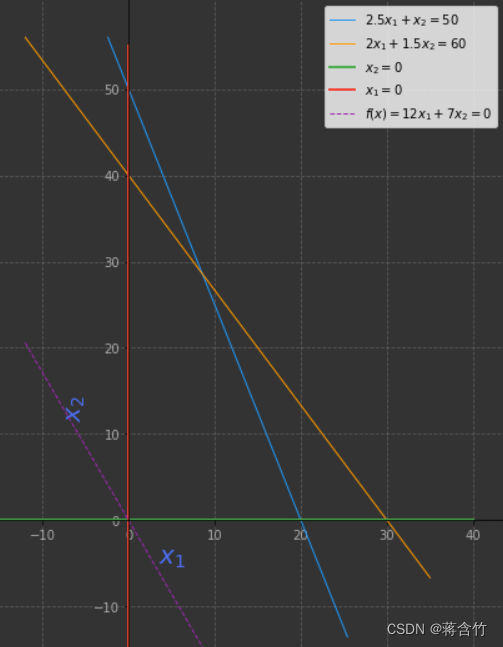
     3. 由约束条件做出的蓝、橙、红、绿线围成的范围，即是我们的有解区域
     4. 将$f(x)=12x_1+7x_2$转换一下，可得$x_2=\frac{-12}{7}{x}_1+\frac{1}{7}f(x)$。当$f(x)=0$时，可做出图中的紫色虚线。
     5. 显然，根据函数的性质，若要使得$\frac{1}{7}f(x)$增大，需将该紫色虚线向上平移
     6. 由图、计算可知，紫线斜率大于蓝线、小于橙线，当且仅当紫色虚线向上平移至过橙色线与蓝色线交点时，$\frac{1}{7}f(x)$取得最大值，即$f(x)$取得最大值
     7. 解 { 2.5 x 1 + x 2 = 50 2 x 1 + 1.5 x 2 = 60
        {2.5x1+x2=502x1+1.5x2=60" role="presentation" style="position: relative;">{2.5x1+x2=502x1+1.5x2=60$$\{\begin{array}{l}2.5x_1+x_2=50\\ 2x_1+1.5x_2=60\end{array}$$
        {2.5x1​+x2​=502x1​+1.5x2​=60​，得 { x 1 = 60 7 x 2 = 200 7
        {x1=607x2=2007" role="presentation" style="position: relative;">{x1=607x2=2007$$\{\begin{array}{l}{x}_1=\frac{60}{7}\\ x_2=\frac{200}{7}\end{array}$$
        {x1​=760​x2​=7200​​
     8. 由于汽车辆数是整数，因此，当生产A车8辆、B车28辆时，可获得最大利益
        f = 12 x 1 + 7 x 2 = 12 ∗ 8 + 28 ∗ 7 = 292
        f=12x1+7x2=12∗8+28∗7=292" role="presentation" style="position: relative;">f=12x1+7x2=12∗8+28∗7=292$$\begin{array}{ll}f& =12x_1+7x_2\\ & =12\ast 8+28\ast 7\\ & =292\end{array}$$
        f​=12x1​+7x2​=12∗8+28∗7=292​

更多数学模型样例

• 线性规划（二）——数学模型样例