数据结构 ----- 插值查找

​
​​

​ 插值查找

活动地址：CSDN21天学习挑战赛

一、折半查找

因为插值查找是根据折半查找优化的一个查找方式，所以在学习插值查找之前要先学习折半查找；

1.1 概念

折半查找又称二分查找，它是一种效率较高的查找方式，但是折半查找的要求较为特殊，折半查找能够作用的条件有两个：顺序存储、表中关键字有序；（也就是说折半查找只能用于存储在顺序表且表内元素也是有序的情况）

1.2 查找过程

• 折半查找进行查找前的第一步是确定一个中间值；
• 用需要查找的元素跟中间值进行比较；
• 如果所查找的元素大于中间值，则在中间值右边的区间进行查找，如果所查找的元素小于中间值，就往中间值左边的区间进行查找，如果等于中间值则代表找到了；
• 经过多次反复如果最终没有找到需要查找的元素，那么就是该元素不在于所查找的表中；

图 1.1

1.3 代码演示

1.3.1

• 第一步将需要查找的元素和所查找的表进行初始化；

图 1.2

1.3.2

• 建立一个方法实现折半查找；
• 方法内传入表、需要查找的元素、所查找表的起始坐标、所查找表的终点坐标；
• 建立一个变量接收返回值；

图 1.3

1.3.3

进行对方法体的编写：

• 如果起始坐标大于终点坐标就代表该表已查询完且为查询到，则返回 -1；
• 定义中间值，中间值的坐标就是起始坐标和终点坐标的和除以二；
• 进行判断如果所查找的元素大于中间值，则代表左边区间都没有该元素，故再进行对方法体的调用将中间值坐标 +1 的坐标传至为起始坐标；
• 进行判断如果所查找的元素小于中间值，则代表右边区间都没有该元素，故再进行对方法体的调用将中间值坐标 -1 的坐标传至为终点坐标；
• 如果所寻找的元素等于中间值，代表已经找到，并传回该坐标值；

图 1.3

1.3.4

• 判断返回值是否为 -1 ；
• 返回值为 -1 表示表内不存在该元素；
• 返回值不为 -1 表示该返回值是所寻找元素的坐标；

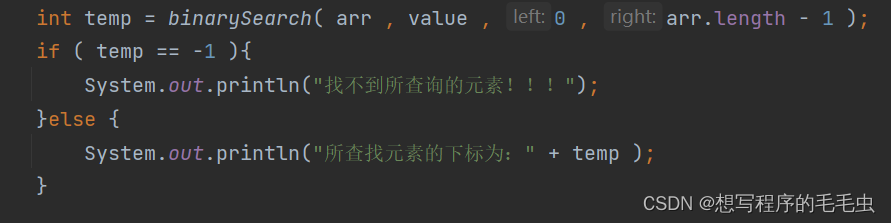
图 1.4

1.4 代码测试

1. 输入一次表内拥有的元素，成功返回下标；
2. 输入一次表内没有的元素，提示不存在该元素；
3. 结论：代码可用无误；

图 1.5

1.5 折半查找代码分享

import java.util.Scanner;

public class test {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int[] arr = { 9 , 10 , 12 , 14 , 15 , 16 , 18 , 20 , 21};
        int value = sc.nextInt();


        int temp = binarySearch( arr , value , 0 , arr.length - 1 );
        if ( temp == -1 ){
            System.out.println("找不到所查询的元素！！！");
        }else {
            System.out.println("所查找元素的下标为：" + temp );
        }
    }

    public static int binarySearch( int[] arr,int value,int left,int right ) {
        if ( left > right ){
            return -1 ;
        }
        int mid = (left + right) / 2;
        if ( value > arr[mid] ){
            return binarySearch( arr, value, mid + 1, right );
        }else if (  value < arr[mid] ){
            return binarySearch( arr, value, left , mid - 1 );
        }else {
            return mid;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

二、插值查找

2.1 概念

插值查找，有序表的一种查找方式；
插值查找是根据查找关键字与查找表中最大最小记录关键字比较后的查找方法；
插值查找基于二分查找，将查找点的选择改进为自适应选择，提高查找效率；

自适应选择点公式：

自适应点 = 起始坐标 + （ 所查找的值 - 起始值 ）/（ 终点值 - 起始值 ）*（ 终点坐标 - 起始坐标 ）

2.2 查找过程

• 根据公式每一次查找自适应值；
• 用需要查找的元素跟自适应值进行比较；
• 如果所查找的元素大于自适应值，则在中间值右边的区间进行查找，如果所查找的元素小于自适应值，就往自适应值左边的区间进行查找，如果等于自适应值则代表找到了；
• 经过多次反复如果最终没有找到需要查找的元素，那么就是该元素不在于所查找的表中；

图 2.1

2.3 代码演示

• 插值插值的代码跟折半查找几乎一模一样，主要的区别就是一个取中间值，一个取自适应值；
• 只需要将公式代入折半查找的代码，那么插值查找就完成了一大半了；
• 但是还有可能出现一种情况，那就是自适应值超出表范围，那么就应该再加一条如果超出范围，直接返回 -1；

图 2.2

2.4 代码测试

1. 查找已有元素时，返回了下标；
2. 查找不存在的元素时，提示没有该元素；
3. 结论：代码可用无误；

图 2.3

2.5 插值查找跟折半查找对比

在方法体增加一条输出，便于在控制台查看进入方法体的次数；

图 2.3

通过控制台我们可以看到，查找同一个元素时，插值查找比折半查找的次数更少，这也是插值查找诞生的由源；

图 2.3

2.6 插值查找代码分享

import java.util.Scanner;

public class demo {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int[] arr = { 9 , 10 , 12 , 14 , 15 , 16 , 18 , 20 , 21};
        int value = sc.nextInt();
        int temp = binarySearch( arr , value , 0 , arr.length - 1 );
        if ( temp == -1 ){
            System.out.println("找不到所查询的元素！！！");
        }else {
            System.out.println("所查找元素的下标为：" + temp );
        }
    }

    public static int binarySearch( int[] arr,int value,int left,int right ) {
        if ( left > right ){
            return -1 ;
        }
        int temp =(int)( left + 1.0 *(value - arr[left]) / (arr[right] - arr[left]) * (right - left) );
        if ( temp < 0 || temp > right){
            return -1;
        }
        if ( value > arr[temp] ){
            return binarySearch( arr, value, temp + 1, right );
        }else if (  value < arr[temp] ){
            return binarySearch( arr, value, left , temp - 1 );
        }else {
            return temp;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33