《算法系列》之位运算

简介

  计算机的世界，不是0就是1，我是指bit。bit作为信息量最基础的的度量单位，也是我们计算机中的基础数据结构。我们在进行应用开发时，常常忘记了梦的开始的地方其实是0和1，而位运算，即对bit位数据进行一元或二元操作的运算，我们做算法题时会发现，合理运用位运算，能大幅提高运算效率。位运算的题还是要需要掌握一定的基础才能方便理解，如果平时只是做上层CURD开发的话，还是要回头捡捡以前的知识。

理论基础

  位操作（Bit Manipulation）是程序设计中对位模式或二进制数的一元和二元操作。在许多古老的微处理器上，位运算比加减运算略快，通常位运算比乘除法运算要快很多。在现代编程语言中，情况并非如此，很多编程语言的解释器都会对基本的运算进行了优化，因此我们在实际开发中可以不必做一些编译器已经帮我们做好的优化，而就写出代码本身所要表现的意思即可。位运算的问题，很多都很有技巧性，大家需要掌握一定的位运算的应用，达到融会贯通的目的。
  程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。 比如，and运算本来是一个逻辑运算符，但整数与整数之间也可以进行and运算。举个例子，6的二进制是110，11的二进制是1011，那么6 and 11的结果就是2，它是二进制对应位进行逻辑运算的结果（0表示False，1表示True，空位都当0处理）。

		1 1 0
and		
	  1 0 1 1
----------------
	  0 0 1 0   =  2
1
2
3
4
5

各位运算在C、C++、Java中的表示方式，其中a、b都是整数。

• and运算 &：相同位的两个数字都为1，则为1，若有一个不为1，则为0。
• or运算 |：相同位只要一个为1即为1。
• xor运算 ^：如果相同位不同则该位为1，否则该位为0。xor运算的逆运算是它本身，也就是说两次异或同一个数最后结果不变，即(a xor b) xor b = a。
• not运算 ~：not运算的定义是把0和1全部取反。
• shl运算 <<：a shl b 就表示把a转为二进制后左移b位（在后面添b个0）。a shl b的值实际上就是a乘以2的b次方，因为在二进制数后添一个0就相当于该数乘以2。通常认为a shl 1比a * 2更快，因为前者是更底层一些的操作。因此程序中乘以2的操作请尽量用左移一位来代替。很多算法和数据结构要求数据规模必须是2的幂，此时可以用shl来定义Max_N等常量。
• shr运算 >>：和shl相似，a shr b表示二进制右移b位（去掉末b位），相当于a除以2的b次方（取整）。也可以用shr 1来代替除以 2，比如二分查找、堆的插入操作等中都可以直接使用。想办法用shr代替除法运算可以使程序效率大大提高。最大公约数的二进制算法用除以2操作来代替慢得出奇的mod运算，效率可以提高60%。

解题心得

• 合理运用位运算，能大幅提高运算效率。
• 位运算的问题，很多都很有技巧性，位运算的题还是要掌握一定的基础才能方便理解。
• 整数也可以进行位运算，相对基础运算，位运算更基础、也更快。
• 异或：相同为0，不同为1。0与任意数异或等于原数。异或同一个数两次，原数不变。
• 异或操作的特性需要重点学习，很多题里有奇效。
• 可以使用左移（<<）和右移（>>）能代替乘以和除以2，可以大幅增加效率。

算法题目

29. 两数相除

题目解析：用位运算代替乘除法，被除数等于商*除数 + 余数，我们除数使用2的k次方进行逼近，然后进行累加，最后即可得到商。
代码如下：

/**
 * 位运算
 */
class Solution {
    public int divide(int dividend, int divisor) {
        if(dividend == 0){
           return 0; 
        }
        if (dividend == Integer.MIN_VALUE && divisor == -1) {
            return Integer.MAX_VALUE;
        }
        boolean neg;
        // 异或计算符号是否相异
        neg = (dividend ^ divisor) < 0;
        long t = Math.abs((long) dividend);
        long d= Math.abs((long) divisor);
        int result = 0;
        for (int i=31; i>=0; i--) {
            if ((t>>i) >= d) { 
                result += 1 << i;
                t -= d << i;
            }
        }
        return neg ? -result : result;//符号相异取反
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

67. 二进制求和

题目解析：先把两个二进制数对齐，然后循环相加两个字符串中相同长度的低位数部分，然后加上carry位，最后反转即可。
代码如下：

/**
 *  char "0" = 48 , "1" =49
 */
class Solution {
    public String addBinary(String a, String b) {
        StringBuilder res = new StringBuilder();
        int i = a.length() - 1;
        int j = b.length() - 1;
        // 进位
        int carry = 0;
        while (i >= 0 || j >= 0) {
            // 把两个二进制数对齐
            int num1 = i >= 0 ? a.charAt(i) - 48 : 0;
            int num2 = j >= 0 ? b.charAt(j) - 48 : 0;
            int sum = num1 + num2 + carry;
            carry = 0;
            if (sum >= 2) {
                sum = sum % 2;
                carry = 1;
            }
            // 先添加后反转，可以减少数组移动时间，从而提高效率
            res.append(sum);
            i--;
            j--;
        }
        if (carry == 1) {
            res.append(1);
        }
        // 反转输出
        return res.reverse().toString();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

89. 格雷编码

题目解析：知道格雷编码的生成原理，也就知道怎么解题了，见以下规则。

格雷编码
公式：G(i) = i ^ (i/2);
如 n = 3:
        G(0) = 000,
        G(1) = 1 ^ 0 = 001 ^ 000 = 001
        G(2) = 2 ^ 1 = 010 ^ 001 = 011
        G(3) = 3 ^ 1 = 011 ^ 001 = 010
        G(4) = 4 ^ 2 = 100 ^ 010 = 110
        G(5) = 5 ^ 2 = 101 ^ 010 = 111
        G(6) = 6 ^ 3 = 110 ^ 011 = 101
        G(7) = 7 ^ 3 = 111 ^ 011 = 100
1
2
3
4
5
6
7
8
9
10
11

代码如下：

/**
 * 位运算
 */
class Solution {
    public List grayCode(int n) {
        List res = new ArrayList<>();
        for (int i = 0; i < 1 << n; ++i) {
            res.add(i ^ i >> 1);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

136. 只出现一次的数字

题目解析：这是一道经典的位运算题，需要讲讲异或的概念了，异或：相同为0，不同为1。0与任意数异或等于原数。异或同一个数两次，原数不变。例如：0 ^ a = a，a ^ b = c，c ^ b = a。就像那，人来人往，只有单身狗会剩下。
代码如下：

/**
 * 位运算
 */
class Solution {
    public int singleNumber(int[] nums) {
        int res = 0;
        for (int n : nums) {
            res ^= n;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

137. 只出现一次的数字 II

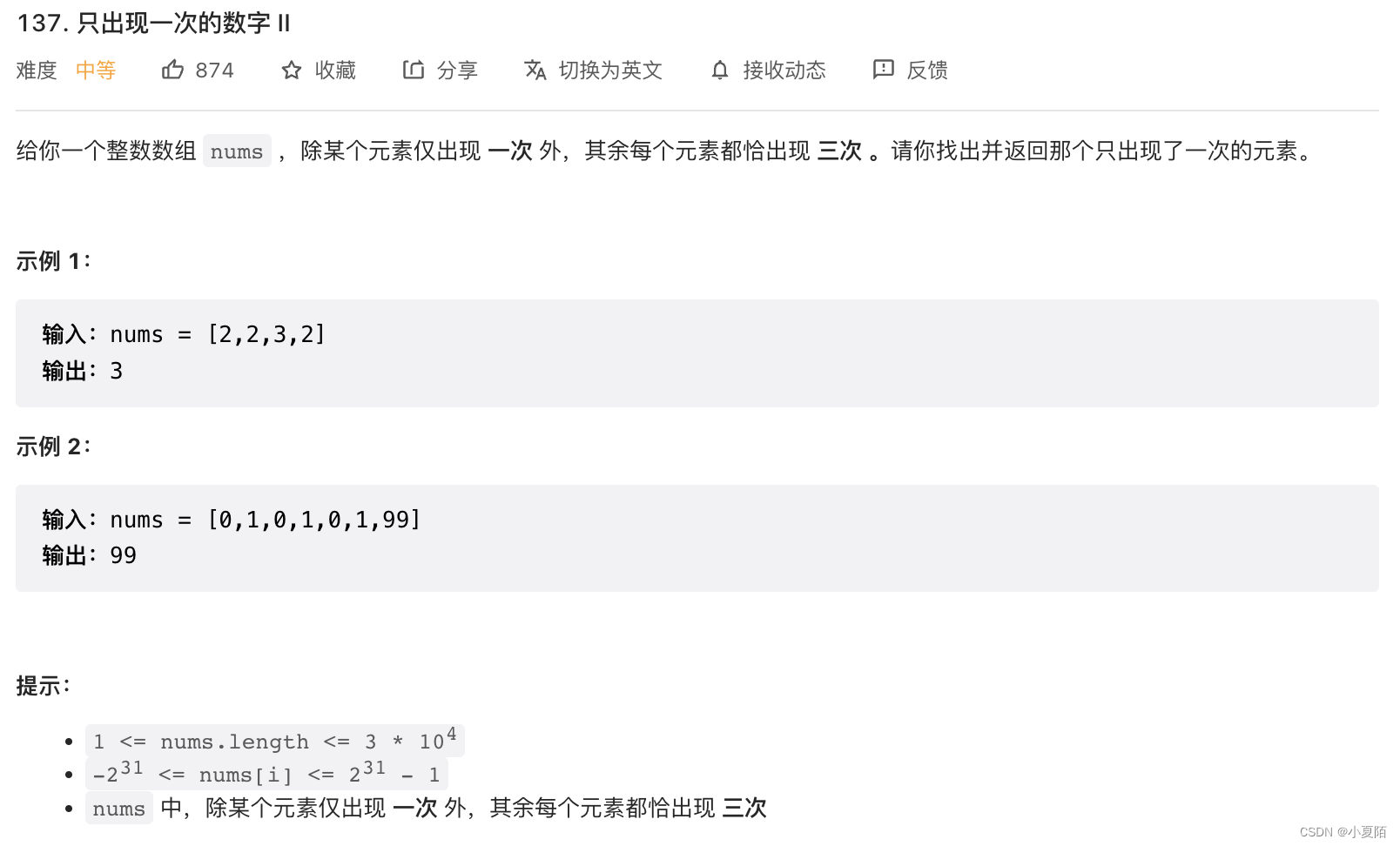
题目解析：需要一个状态转换电路，使得一个数出现3次时能自动抵消为0，最后剩下的就是只出现1次的数。

有如下规律：
 0 ^ x = x,
 x ^ x = 0；
 x & ~x = 0,
 x & ~0 = x;
1
2
3
4
5

x第一次出现后，a = (a ^ x) &~b的结果为 a = x， b = (b ^ x) & ~a的结果因为此时因为a = x了，所以b = 0。
x第二次出现：a = (a ^ x) & ~b， a = (x ^ x) & ~0， a = 0； b = (b ^ x) & ~a 化简， b = (0 ^ x) & ~0 ，b = x。
x第三次出现：a = (a ^ x) & ~b， a = (0 ^ x) & ~x ，a = 0；b = (b ^ x) & ~a 化简， b = (x ^ x) & ~0 ，b = 0；所以出现三次同一个数，a和b最终都变回了0。
只出现一次的数，按照上面x第一次出现的规律可知a = x，b = 0；因此最后返回a。
代码如下：

/**
 * 位运算
 */
class Solution {
    public int singleNumber(int[] nums) {
        int a = 0, b = 0;
        for (int num: nums) {
            a = (a ^ num) & ~b;
            b = (b ^ num) & ~a;
        }
        return a;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

190. 颠倒二进制位

题目解析：从低位往高位枚举 n 的每一位，将其倒序添加到翻转结果 rev 中。
代码如下：

/**
 * 位运算
 */
public class Solution {
    public int reverseBits(int n) {
        int rev = 0;
        for (int i = 0; i < 32 && n != 0; ++i) {
            rev |= (n & 1) << (31 - i);
            n >>>= 1;
        }
        return rev;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

191. 位1的个数

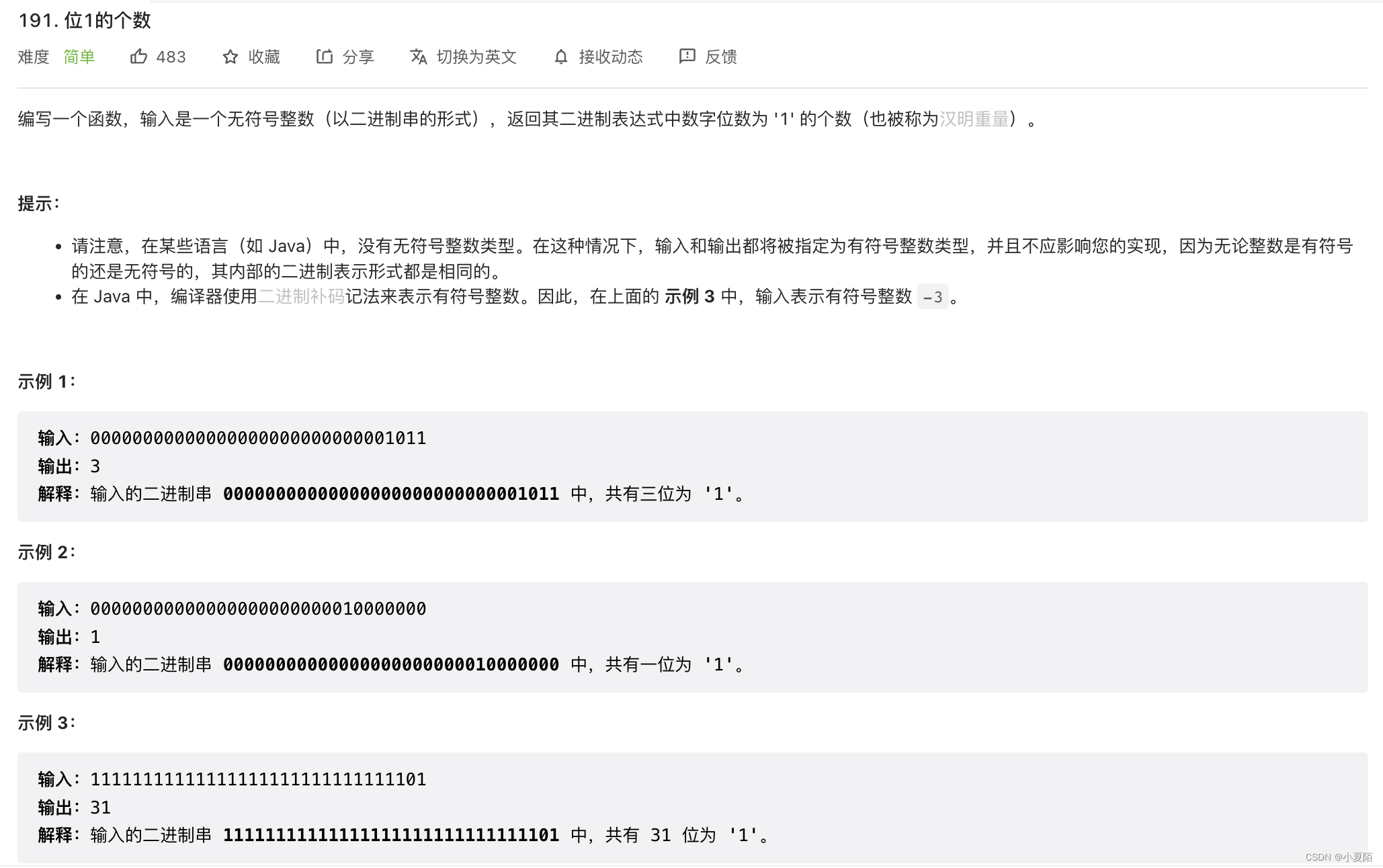
题目解析：与 1 << i 依次进行 & 运算，即可判断当前数字i位是否为1。
代码如下：

/**
 * 位运算
 */
public class Solution {
    public int hammingWeight(int n) {
        int ret = 0;
        for (int i = 0; i < 32; i++) {
            if ((n & (1 << i)) != 0) {
                ret++;
            }
        }
        return ret;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

201. 数字范围按位与

题目解析：用右移的方式，找到最长公共前缀即可。
代码如下：

/**
 * 位运算 
 */
class Solution {
    public int rangeBitwiseAnd(int m, int n) {
        int shift = 0;
        // 找到公共前缀
        while (m < n) {
            m >>= 1;
            n >>= 1;
            ++shift;
        }
        return m << shift;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

231. 2 的幂

题目解析：如果一个数是2的幂，则它的二进制为100000…，1后n个零。
代码如下：

/**
 * 位运算
 */
class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n <= 0){
            return false;
        }
        // 与减1的二进制做且运算，如果是2的幂，则结果一定为0
        return ( n & (n-1)) == 0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

260. 只出现一次的数字 III

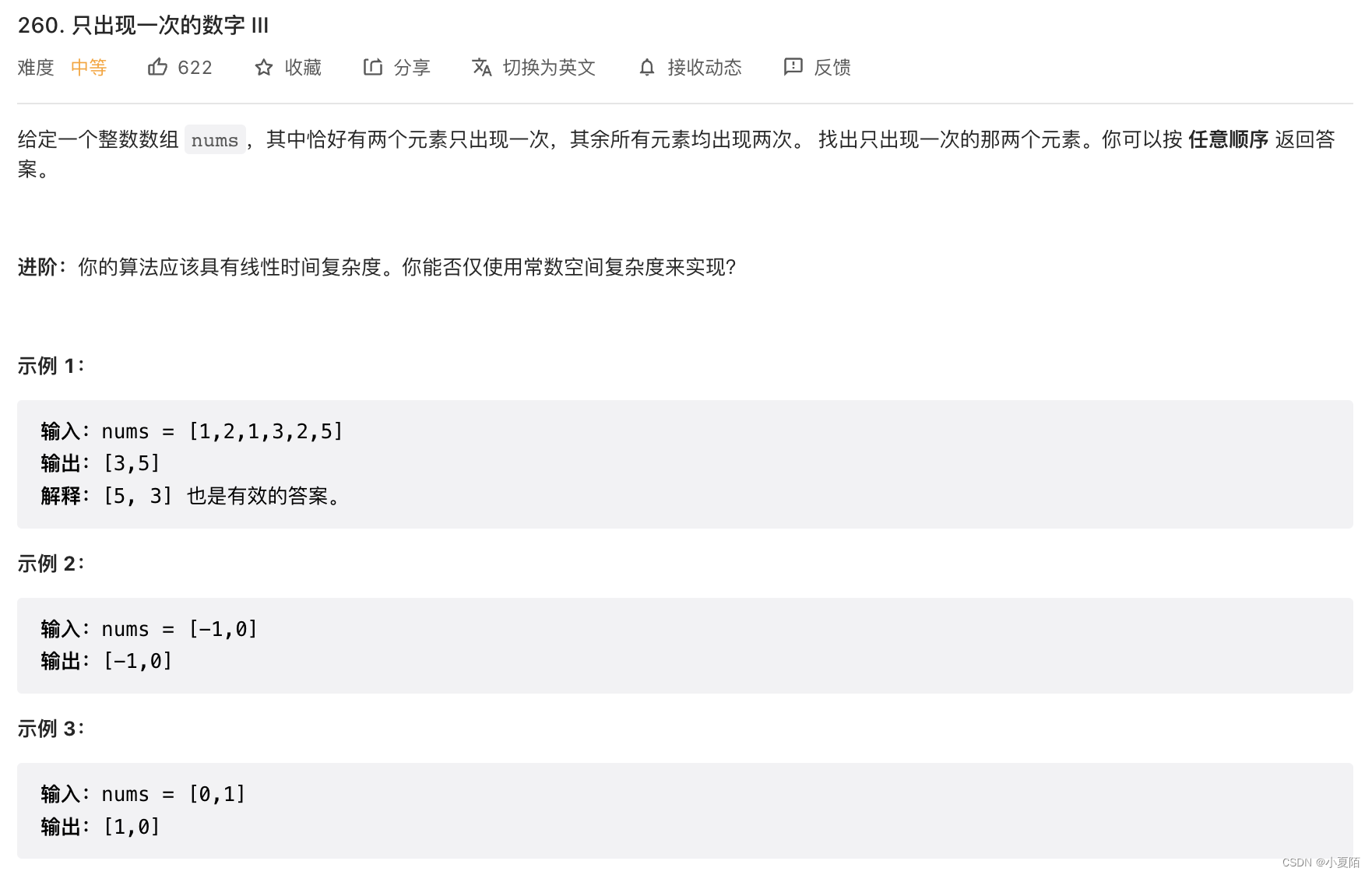
题目解析：异或操作，首先异或整个数组，剩下x和y的异或结果，然后找到结果二进制为1的位，此位能将数组分为两部分，一部分包括x，一部分包括y和其它出现两次的数，分别对x和y的异或结果求异或操作，即可得出结果。
代码如下：

/**
 * 位运算
 */
class Solution {
    public int[] singleNumber(int[] nums) {
        int a= 0;
        for (int num : nums) {
            a ^= num;
        }
        int i = 0;
        for (; i <31 ; i++) {
            if ((a>>i&1)==1)
                break;
        }
        int x=0, y = 0;
        for (int num : nums) {
            if ((num>>i&1)==0)
                x^=num;
            else
                y^=num;
        }
        return new int[]{x,y};
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

268. 丢失的数字

题目解析：还是异或操作，使用异或操作的特性：相同为0，不同为1。0与任意数异或等于原数。异或同一个数两次，原数不变。
代码如下：

/**
 * 位运算
 */
class Solution {
    public int missingNumber(int[] nums) {
        int res = 0, index = 1;
        for (int num : nums)
            res ^= num ^ index++;
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11

回到首页

刷 leetcode 500+ 题的一些感受

下一篇

[xxxxx]