数据结构-非线性结构-集合-树（一般树-二叉树）-图（有向图、无向图）

一般树

概述

• 概念：
  树是n个（n>=0）有限结点组成的具有层次关系的集合，n=0时，是空树；

任意非空树应该满足的条件：

• 有且仅有一个特定的被称为根的节点；
• 当n>1时，其余节点可以分为m（m>0）个互不相交的有限集合，其中每一个集合本身又是一棵树，称为根节点的子树。

n个节点的树有n-1条边；

性质
树中的节点数 = 所有节点的度数 加 1

基本术语

度
树中各结点度的最大值称为该树的度。
树中一个结点的子结点的个数称为该结点的度。

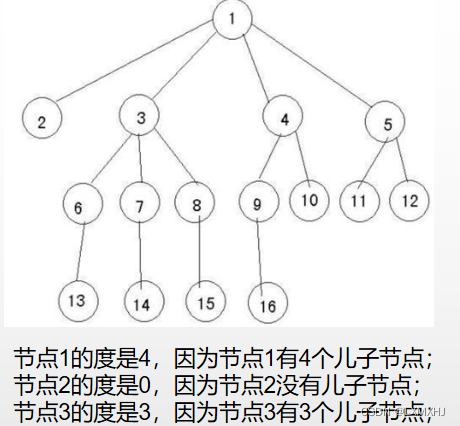
分支结点和叶子结点
度大于0的结点 称为 分支结点；
度为0的节点 称为 叶子结点。

层次、高度、深度

有序树和无序树

路径
树中两个结点之间的路径是由两个结点之间所经过的结点序列构成的。

路径长度：路径上所经历边的个数；

森林
m（m>=0）棵互不相交的树的集合 。

二叉树

概述

• 二叉树
  每个节点至多只有二棵子树，左子树和右子树，次序不能颠倒。

• 逻辑上分类
  空二叉树、只有一个根结点的二叉树、只有左子树、只有右子树、完全二叉树(特例：满二叉树)。
  

• 遍历二叉树
  按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次，有前序、中序、后序遍历。
  前序 = 根左右；中序 = 左根右；后序 = 左右根。
  

• 二叉查找树（二叉搜索树）
  为了解决数据库索引排好序的原则而提出。
  在满足二叉树的条件下，左子树的节点值总是小于根的节点值，右子树的节点值总是大于根的节点值，也就是左子树节点值 < 根的节点值 < 右子树节点值。
  但是二叉查找树构建可能极不平衡，最后构建成了一个链表。

• 平衡二叉树（AVL树）
  为了解决二叉查找树构建极不平衡的情况。提出。
  符合二叉查找树的定义，其次必须满足任何节点的两个子树的高度之差的绝对值不超过 1。
  当数据量过多时，二叉树高度会越来越高，1000个数据有9-10层，那么可能找一个数据需要9-10次IO。
  就会出现平衡二叉树高度过高导致的IO问题。提出B-tree 和 B+tree

• B-tree
  每个节点上多放一些元素，减少磁盘IO。
  多路搜索树；

• B+tree
  是B-tree树的变体，是一种多路搜索树；

性质

若根的层次为1，则二叉树的第i层最多有2^i-1个节点；
一棵非空二叉树，叶子节点数 = 度为2
不属于二叉树的是：B树，它是多叉树；
而AVL树、二叉排序树、哈夫曼树都是二叉树。

B-tree

• 特性：
  关键字集合分布在整颗树中；
  任何一个关键字只能出现在一个结点中；
  搜索有可能在非叶子结点结束；
  搜索性能等价于在关键字全集内做一次二分查找；
  自动层次控制：
  由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少利用率，其最底搜索性能为：O（logN）；

B+tree

图示：

作用：
优势= 更加高效的单元素查找。

图

概述

• 概念
  图 = 一些顶点的集合，顶点通过一系列边连接。

• 为什么使用图？
  有些编程问题可以通过顶点和边表示出来，图算法 = 广度优先搜索 或 深度优先搜索。

• 分类
  根据各元素之前的联系单双向：有向图 和 无向图。
  有向图 = 各元素之间的联系是单向的；
  无向图 = 各元素之间的联系是双向的。