• 算法设计 - 分治法

    目录

    分治法

    什么是分治法

    分治思想和递归

    分治法的适用条件

    分治法实例

    快速排序

    快速排序的原理

    快速排序的最优和最差情况下的时间复杂度推导

    快速排序的实现 - 双边循环

    快速排序的实现 - 单边循环

    快速排序的优化 - 打乱有序数组

    归并排序

    归并排序和中国好声音晋级机制

    归并排序的原理

    归并排序的实现

    归并排序的时间复杂度

    归并排序的非递归实现

    分治法

    什么是分治法

    分治法，即运用分治思想来设计算法。

    分治思想和递归

    分治思想，即将大的问题分解成多个小问题，然后通过解决小问题，再将小问题的解合并为大问题的解。即中国古代“分而治之”的策略。

    分治思想的实现依赖于递归，递归思想的本质就是分治思想。也就是说分治思想和递归二者是相辅相成的。

    想要学好分治法，最好先学习递归

    算法设计 - 递归_伏城之外的博客-CSDN博客

    分治法的适用条件

    1. 该问题的规模小到一定的程度就可以轻松求解（存在base case，即递归出口）
    2. 该问题可以分为若干个规模较小的相同问题，并分解出来的问题的解可以合并为原始问题的解（能够relate hard case to simple case，即存在递归公式）
    3. 该问题所分解出的各个子问题是相互独立的，即子问题之间不好含公共的子问题（避免无意义的重复递归）

    分治法实例

    快速排序

    快速排序的原理

    快速排序是基于分治思想设计的排序算法。

    快速排序分解逻辑如下：

    1. 选取无序数组中任意一个元素作为基准值pivot，遍历其他数组元素：
    2. 将比pivot值大的数组元素放到pivot元素的右边
    3. 将比pivot值小的数组元素放到pivot元素的左边
    4. 此时pivot元素处于有序位置，但是pivot左边所有数组元素、pivot右边所有数组元素任然处于无序状态。
    5. 将pivot左边所有数组元素当成一个无序子数组、pivot右边所有数组元素当一个无序子数组，重复上述逻辑
    6. 当子数组只有一个元素，就可以退出上述逻辑

    如下图，所以每次都取无序数组的首元素为基准值，将比基准值小的元素放到其左边，将比基准值大的元素放到其右边。

    按此分解逻辑，一个无序数组，将会被拆分两个无序子数组和一个有序元素，而无序子数组又重复此分解逻辑，直到子数组本身只有一个元素无法拆分时。

    而分解的最终结果就是所有的元素都处于有序位置。

    此时也就达到了排序目的，而无需合并操作了。

    快速排序的最优和最差情况下的时间复杂度推导

    快速排序最优的情况是，每次数组拆分出来的两个子数组元素数目都是相等的，此时快速排序时间复杂度为：

    • 第1轮需要拆分1次，每次约遍历n个元素
    • 第2轮需要拆分2次，每次约遍历n/2个元素
    • 第3轮需要拆分4次，每次约遍历n/4个元素
    • 第4轮需要拆分8次，每次约遍历n/8个元素
    • ......
    • 第x轮需要拆分2^(x-1)次，每次约遍历n/2^(x-1)个元素，假设此时每个子数组元素个数为1，即每次只需要遍历1个元素，即 n/2^(x-1) = 1，则 x = logn + 1 ≈ logn

    当n接近无穷大时，则每轮近似要遍历n个元素，一共要遍历 logn轮，所以时间复杂度为O(nlogn)

     快速排序最差的情况是，数组本身就是有序的，此时

    • 第1轮需要拆分1次（得到一个子数组长度为0，一个子数组长度为n-1），一共约遍历n个元素
    • 第2轮需要拆分1次（同上），一共约遍历n-1个元素
    • 第3轮需要拆分1次（同上），一共约遍历n-2个元素
    • ......
    • 第x轮需要拆分1次，一共约遍历1个元素

    即：总共需要遍历  1 + 2 + 3 +...+ (n-2) + (n-1) + n = n * (n+1) / 2

    当n接近无穷大时，时间复杂度约为O（n^2）

    快速排序的实现 - 双边循环

    快速排序的实现方式分为两种：双边循环、单边循环。

    双边循环实现：

    1. /* JavaScript Node ACM模式 控制台输入获取 */
    2. const readline = require("readline");
    3.  
    4. const rl = readline.createInterface({
    5.   input: process.stdin,
    6.   output: process.stdout,
    7. });
    8. rl.on("line", (line) => {
    9.   const arr = line.split(",");
    10.   quickSort(arr); // 4,7,2,0,9,6,8,1,3,5
    11. });
    12.  
    13. /* 快速排序算法 */
    14. function quickSort(arr, start = 0, end = arr.length - 1) {
    15.   if (start >= end) {
    16.     return;
    17.   }
    18.  
    19.   let pivot = arr[start];
    20.   let left = start;
    21.   let right = end;
    22.   console.log(`pivot=${pivot}, left=${left}, right=${right}`); // test
    23.   visibleCursor(arr, left, right); // test
    24.  
    25.   while (left !== right) {
    26.     while (right > left && arr[right] >= pivot) {
    27.       right--;
    28.       visibleCursor(arr, left, right); // test
    29.     }
    30.  
    31.     while (left < right && arr[left] <= pivot) {
    32.       left++;
    33.       visibleCursor(arr, left, right); // test
    34.     }
    35.  
    36.     if (right > left) {
    37.       let tmp = arr[right];
    38.       arr[right] = arr[left];
    39.       arr[left] = tmp;
    40.       visibleCursor(arr, left, right); // test
    41.     }
    42.   }
    43.  
    44.   arr[start] = arr[left];
    45.   arr[left] = pivot;
    46.   visibleCursor(arr, left, right); // test
    47.  
    48.   quickSort(arr, start, left - 1);
    49.   quickSort(arr, left + 1, end);
    50. }
    51.  
    52. /* left、right游标打印 */
    53. function visibleCursor(arr, left, right) {
    54.   console.log(arr.join(" "));
    55.   console.log(
    56.     arr
    57.       .slice()
    58.       .map((_, index) => {
    59.         if (index === left) {
    60.           if (left === right) {
    61.             return "↑";
    62.           }
    63.           return "L";
    64.         } else if (index === right) {
    65.           return "R";
    66.         } else {
    67.           return " ";
    68.         }
    69.       })
    70.       .join(" ")
    71.   );
    72. }

    双边循环快速排序，指的是使用两个游标left、right来界定左子数组范围、右子数组范围，left游标左边的就是左子数组，right游标右边的就是右子数组。

    left、right游标工作原理如下：

    初始时，left游标指向数组头部位置，代表左子数组暂无元素，right游标指向数组尾部位置，代表右子数组暂无元素。

    之后，right游标开始向左游动，当right游标指向的数组元素小于pivot基准值时（表示该元素应该被放到左子数组中），则暂停游动，否则保持游动，直到right和left相遇才停止游动。

    当right游标暂停游动时，left游标开始向右移动，当left游标指向的数组元素大于pivot基准时（表示该元素应该被放到右子数组中），则暂停游动，否则保持游动，直到left和right相遇才停止游动。

    当left、right都暂停游动时，判断

    • 若left === right，则停止游动
    • 若left !== right，则直接交换arr[left]和arr[right]值，继续当前数组的下一轮游动

    当left、right都停止游动时，则此时left必然等于right，我们需要将arr[left/right]的元素值和arr[start]元素值交换。

    此时我们会得到两个子数组，分别是 [0，left-1]数组索引范围，和[left+1，arr.length-1]数组索引范围，然后对这两个子数组分别进行双边循环快排，直到子数组只有一个元素时，退出快排。

    具体实例，请看下面的运行日志，L代表游标left，R代表游标right

    1. PS D:\Desktop\DS> node .\haha.js
    2. 4,7,2,0,9,6,8,1,3,5
    3. pivot=4, left=0, right=9
    4. 4 7 2 0 9 6 8 1 3 5     //如果R指向值小于pivot，则暂停左移，否则保持左移
    5. L                 R     
    6. 4 7 2 0 9 6 8 1 3 5     //arr[R] = 3 < 4，R暂停左移，若R暂停左移，则L开始右移
    7. L               R  
    8. 4 7 2 0 9 6 8 1 3 5     //如果L指向值大于pivot，则暂停右移，否则保持左移，此时arr[L]= 7 > 4
    9.   L             R       
    10. 4 3 2 0 9 6 8 1 7 5     //R、L都暂停移动时，若 R > L，则交换对应元素的值
    11.   L             R       
    12. 4 3 2 0 9 6 8 1 7 5     
    13.   L           R         
    14. 4 3 2 0 9 6 8 1 7 5     
    15.     L         R         
    16. 4 3 2 0 9 6 8 1 7 5     
    17.       L       R         
    18. 4 3 2 0 9 6 8 1 7 5     
    19.         L     R         
    20. 4 3 2 0 1 6 8 9 7 5     
    21.         L     R         
    22. 4 3 2 0 1 6 8 9 7 5     
    23.         L   R           
    24. 4 3 2 0 1 6 8 9 7 5     
    25.         L R             
    26. 4 3 2 0 1 6 8 9 7 5     // 当R、L指向同一个位置时，则停止游动，交换arr[start]和arr[L]的值
    27.         ↑               
    28. 1 3 2 0 4 6 8 9 7 5     // 此时L游标往左就是左子数组（不含L），R游标往右就是右子数组（不含R）
    29.         ↑               
    30. pivot=1, left=0, right=3
    31. 1 3 2 0 4 6 8 9 7 5     
    32. L     R                 
    33. 1 3 2 0 4 6 8 9 7 5     
    34.   L   R                 
    35. 1 0 2 3 4 6 8 9 7 5     
    36.   L   R                 
    37. 1 0 2 3 4 6 8 9 7 5     
    38.   L R                   
    39. 1 0 2 3 4 6 8 9 7 5     
    40.   ↑                     
    41. 0 1 2 3 4 6 8 9 7 5
    42.   ↑
    43. pivot=2, left=2, right=3
    44. 0 1 2 3 4 6 8 9 7 5
    45.     L R
    46. 0 1 2 3 4 6 8 9 7 5
    47.     ↑
    48. 0 1 2 3 4 6 8 9 7 5
    49.     ↑
    50. pivot=6, left=5, right=9
    51. 0 1 2 3 4 6 8 9 7 5
    52.           L       R
    53. 0 1 2 3 4 6 8 9 7 5
    54.             L     R
    55. 0 1 2 3 4 6 5 9 7 8
    56.             L     R
    57. 0 1 2 3 4 6 5 9 7 8
    58.             L   R
    59. 0 1 2 3 4 6 5 9 7 8
    60.             L R
    61. 0 1 2 3 4 6 5 9 7 8
    62.             ↑
    63. 0 1 2 3 4 5 6 9 7 8
    64.             ↑
    65. pivot=9, left=7, right=9
    66. 0 1 2 3 4 5 6 9 7 8
    67.               L   R
    68. 0 1 2 3 4 5 6 9 7 8
    69.                 L R
    70. 0 1 2 3 4 5 6 9 7 8
    71.                   ↑
    72. 0 1 2 3 4 5 6 8 7 9
    73.                   ↑
    74. pivot=8, left=7, right=8
    75. 0 1 2 3 4 5 6 8 7 9
    76.               L R
    77. 0 1 2 3 4 5 6 8 7 9
    78.                 ↑
    79. 0 1 2 3 4 5 6 7 8 9
    80.                 ↑

    快速排序的实现 - 单边循环

    单边循环实现：

    1. /* JavaScript Node ACM模式 控制台输入获取 */
    2. const readline = require("readline");
    3.  
    4. const rl = readline.createInterface({
    5.   input: process.stdin,
    6.   output: process.stdout,
    7. });
    8. rl.on("line", (line) => {
    9.   const arr = line.split(",");
    10.   quickSort(arr); // 4,7,2,0,6,8,1,3,5
    11. });
    12.  
    13. /* 快速排序算法 */
    14. function quickSort(arr, start = 0, end = arr.length - 1) {
    15.   if (start >= end) {
    16.     return;
    17.   }
    18.  
    19.   let mark = start;
    20.   let pivot = arr[start];
    21.   console.log(`pivot=${pivot}, start=${start}, end=${end}`); // test
    22.  
    23.   for (let i = start + 1; i <= end; i++) {
    24.     visibleCursor(arr, mark, i); // test
    25.     if (arr[i] < pivot) {
    26.       mark++;
    27.       visibleCursor(arr, mark, i); // test
    28.       let tmp = arr[mark];
    29.       arr[mark] = arr[i];
    30.       arr[i] = tmp;
    31.       visibleCursor(arr, mark, i); // test
    32.     }
    33.   }
    34.  
    35.   arr[start] = arr[mark];
    36.   arr[mark] = pivot;
    37.   visibleCursor(arr, mark); // test
    38.  
    39.   quickSort(arr, start, mark - 1);
    40.   quickSort(arr, mark + 1, end);
    41. }
    42.  
    43. /* mark游标打印 */
    44. function visibleCursor(arr, mark, i) {
    45.   console.log(arr.join(" "));
    46.   console.log(
    47.     arr
    48.       .slice()
    49.       .map((_, index) => {
    50.         if (index === mark) {
    51.           return "m";
    52.         } else if (index === i) {
    53.           return "i";
    54.         } else {
    55.           return " ";
    56.         }
    57.       })
    58.       .join(" ")
    59.   );
    60. }

    单边循环快速排序，指的是只依赖于于一个游标mark来界定左右子数组的范围，mark游标左边的范围就是左子数组，mark游标右边的范围就是右子数组。

     mark游标无法单独进行工作，需要搭配for循环遍历数组元素的i指针同时工作才可以。

    下面是mark游标和for循环i指针的工作原理：

    初始时，mark指针指向数组头部位置，for循环从数组第二个元素开始遍历

    for循环每遍历一个数组元素，都要和pivot基准值进行比较，若比pivot小，则意味着左子数组长度+1，即mark游标此时需要向右移动一位

    然后交换mark指向的元素 和 for循环此时遍历的元素，即i指针指向的元素

    之后，继续下一次循环，直到for循环遍历结束

    需要注意的是，mark指向的元素是比pivot小的元素，所以最后需要将mark指向的元素和arr[start]元素交换位置。

    此时mark游标左边都是比pivot小的元素，即形成左子数组，右边都是比pivot大的元素，即形成右子数组。

    分别将左子数组和右子数组投入单边循环快排。直到子数组只有一个元素时，退出快排。

    具体实例，请看下面的运行日志，m代表游标mark，i代表for循环指针。

    1. PS D:\Desktop\DS> node .\haha.js
    2. 4,7,2,0,6,8,1,3,5
    3. pivot=4, start=0, end=8
    4. 4 7 2 0 6 8 1 3 5      // 初始时，m指向数组第一个元素，for循环指针i从数组第二个元素开始
    5. m i                    
    6. 4 7 2 0 6 8 1 3 5      // for循环开始遍历数组元素
    7. m   i                  
    8. 4 7 2 0 6 8 1 3 5      // 若for循环指针i遍历到的值小于pivot，则m++，表示拓展左子数组长度
    9.   m i                  
    10. 4 2 7 0 6 8 1 3 5      // 然后交换arr[m]和arr[i]的位置，让小于pivot的值加入到左子数组中
    11.   m i                  
    12. 4 2 7 0 6 8 1 3 5      // 交换完成后，继续for循环
    13.   m   i                
    14. 4 2 7 0 6 8 1 3 5      
    15.     m i                
    16. 4 2 0 7 6 8 1 3 5      
    17.     m i                
    18. 4 2 0 7 6 8 1 3 5      
    19.     m   i              
    20. 4 2 0 7 6 8 1 3 5      
    21.     m     i            
    22. 4 2 0 7 6 8 1 3 5      
    23.     m       i          
    24. 4 2 0 7 6 8 1 3 5      
    25.       m     i          
    26. 4 2 0 1 6 8 7 3 5      
    27.       m     i          
    28. 4 2 0 1 6 8 7 3 5      
    29.       m       i        
    30. 4 2 0 1 6 8 7 3 5      
    31.         m     i        
    32. 4 2 0 1 3 8 7 6 5      
    33.         m     i        
    34. 4 2 0 1 3 8 7 6 5      // 当for循环结束时，m右边都是大于pivot的值，而m左边除了第一个元素外
    35.         m       i      
    36. 3 2 0 1 4 8 7 6 5      // 都是小于pivot的值，而m自身指向的元素是小于pivot的值，所以交换arr[m]和arr[start]的值
    37.         m              
    38. pivot=3, start=0, end=3
    39. 3 2 0 1 4 8 7 6 5      
    40. m i                    
    41. 3 2 0 1 4 8 7 6 5
    42.   m
    43. 3 2 0 1 4 8 7 6 5
    44.   m
    45. 3 2 0 1 4 8 7 6 5
    46.   m i
    47. 3 2 0 1 4 8 7 6 5
    48.     m
    49. 3 2 0 1 4 8 7 6 5
    50.     m
    51. 3 2 0 1 4 8 7 6 5
    52.     m i
    53. 3 2 0 1 4 8 7 6 5
    54.       m
    55. 3 2 0 1 4 8 7 6 5
    56.       m
    57. 1 2 0 3 4 8 7 6 5
    58.       m
    59. pivot=1, start=0, end=2
    60. 1 2 0 3 4 8 7 6 5
    61. m i
    62. 1 2 0 3 4 8 7 6 5
    63. m   i
    64. 1 2 0 3 4 8 7 6 5
    65.   m i
    66. 1 0 2 3 4 8 7 6 5
    67.   m i
    68. 0 1 2 3 4 8 7 6 5
    69.   m
    70. pivot=8, start=5, end=8
    71. 0 1 2 3 4 8 7 6 5
    72.           m i
    73. 0 1 2 3 4 8 7 6 5
    74.             m
    75. 0 1 2 3 4 8 7 6 5
    76.             m
    77. 0 1 2 3 4 8 7 6 5
    78.             m i  
    79. 0 1 2 3 4 8 7 6 5
    80.               m
    81. 0 1 2 3 4 8 7 6 5
    82.               m
    83. 0 1 2 3 4 8 7 6 5
    84.               m i
    85. 0 1 2 3 4 8 7 6 5
    86.                 m
    87. 0 1 2 3 4 8 7 6 5
    88.                 m
    89. 0 1 2 3 4 5 7 6 8
    90.                 m
    91. pivot=5, start=5, end=7
    92. 0 1 2 3 4 5 7 6 8
    93.           m i
    94. 0 1 2 3 4 5 7 6 8
    95.           m   i
    96. 0 1 2 3 4 5 7 6 8
    97.           m
    98. pivot=7, start=6, end=7
    99. 0 1 2 3 4 5 7 6 8
    100.             m i
    101. 0 1 2 3 4 5 7 6 8
    102.               m
    103. 0 1 2 3 4 5 7 6 8
    104.               m
    105. 0 1 2 3 4 5 6 7 8
    106.               m

    快速排序的优化 - 打乱有序数组

    如果一个数组本身就是有序的，然后对他进行快速排序，则此时时间复杂度会变为O(n^2)，为了避免这种极端情况，我们需要随机打乱原数组的排序，来避免快速排序一个有序数组。

    我们以双边循环为例，来改进算法

    1. /* JavaScript Node ACM模式 控制台输入获取 */
    2. const readline = require("readline");
    3.  
    4. const rl = readline.createInterface({
    5.   input: process.stdin,
    6.   output: process.stdout,
    7. });
    8.  
    9. rl.on("line", (line) => {
    10.   const arr = line.split(",");
    11.   quickSort(arr); // 1,2,3,4,5,6,7,8,9
    12.  
    13. /* 快速排序算法 */
    14. function quickSort(arr, start = 0, end = arr.length - 1) {
    15.   if (start >= end) {
    16.     return;
    17.   }
    18.  
    19.   randomSwap(arr, start, end); // 每次快排前，将数组指定范围内的首元素和其他元素交换，避免快排一个有序数列
    20.  
    21.   let pivot = arr[start];
    22.   let left = start;
    23.   let right = end;
    24.   console.log(`pivot=${pivot}, left=${left}, right=${right}`); // test
    25.   visibleCursor(arr, left, right); // test
    26.  
    27.   while (left !== right) {
    28.     while (right > left && arr[right] >= pivot) {
    29.       right--;
    30.       visibleCursor(arr, left, right); // test
    31.     }
    32.  
    33.     while (left < right && arr[left] <= pivot) {
    34.       left++;
    35.       visibleCursor(arr, left, right); // test
    36.     }
    37.  
    38.     if (right > left) {
    39.       let tmp = arr[right];
    40.       arr[right] = arr[left];
    41.       arr[left] = tmp;
    42.       visibleCursor(arr, left, right); // test
    43.     }
    44.   }
    45.  
    46.   arr[start] = arr[left];
    47.   arr[left] = pivot;
    48.   visibleCursor(arr, left, right); // test
    49.  
    50.   quickSort(arr, start, left - 1);
    51.   quickSort(arr, left + 1, end);
    52. }
    53.  
    54. /* 打乱有序数列 */
    55. function randomSwap(arr, start, end) {
    56.   console.log("before swap:" + arr);
    57.   const diff = end - start + 1;
    58.   const index = Math.floor(Math.random() * diff);
    59.   let tmp = arr[start + index];
    60.   arr[start + index] = arr[start];
    61.   arr[start] = tmp;
    62.   console.log("after swap:" + arr);
    63. }
    64.  
    65. /* left、right游标打印 */
    66. function visibleCursor(arr, left, right) {
    67.   console.log(arr.join(" "));
    68.   console.log(
    69.     arr
    70.       .slice()
    71.       .map((_, index) => {
    72.         if (index === left) {
    73.           if (left === right) {
    74.             return "↑";
    75.           }
    76.           return "L";
    77.         } else if (index === right) {
    78.           return "R";
    79.         } else {
    80.           return " ";
    81.         }
    82.       })
    83.       .join(" ")
    84.   );
    85. }
    1. PS D:\Desktop\DS> node .\haha.js
    2. 1,2,3,4,5,6,7,8,9
    3. before swap:1,2,3,4,5,6,7,8,9
    4. after swap:5,2,3,4,1,6,7,8,9 
    5. pivot=5, left=0, right=8     
    6. 5 2 3 4 1 6 7 8 9
    7. L               R
    8. 5 2 3 4 1 6 7 8 9
    9. L             R  
    10. 5 2 3 4 1 6 7 8 9
    11. L           R    
    12. 5 2 3 4 1 6 7 8 9
    13. L         R      
    14. 5 2 3 4 1 6 7 8 9
    15. L       R        
    16. 5 2 3 4 1 6 7 8 9
    17.   L     R        
    18. 5 2 3 4 1 6 7 8 9
    19.     L   R        
    20. 5 2 3 4 1 6 7 8 9
    21.       L R        
    22. 5 2 3 4 1 6 7 8 9
    23.         ↑        
    24. 1 2 3 4 5 6 7 8 9
    25.         ↑        
    26. before swap:1,2,3,4,5,6,7,8,9
    27. after swap:2,1,3,4,5,6,7,8,9 
    28. pivot=2, left=0, right=3     
    29. 2 1 3 4 5 6 7 8 9
    30. L     R
    31. 2 1 3 4 5 6 7 8 9
    32. L   R
    33. 2 1 3 4 5 6 7 8 9
    34. L R
    35. 2 1 3 4 5 6 7 8 9
    36.   ↑
    37. 1 2 3 4 5 6 7 8 9
    38.   ↑
    39. before swap:1,2,3,4,5,6,7,8,9
    40. after swap:1,2,3,4,5,6,7,8,9 
    41. pivot=3, left=2, right=3
    42. 1 2 3 4 5 6 7 8 9
    43.     L R
    44. 1 2 3 4 5 6 7 8 9
    45.     ↑
    46. 1 2 3 4 5 6 7 8 9
    47.     ↑
    48. before swap:1,2,3,4,5,6,7,8,9
    49. after swap:1,2,3,4,5,8,7,6,9
    50. pivot=8, left=5, right=8
    51. 1 2 3 4 5 8 7 6 9
    52.           L     R
    53. 1 2 3 4 5 8 7 6 9
    54.           L   R
    55. 1 2 3 4 5 8 7 6 9
    56.             L R
    57. 1 2 3 4 5 8 7 6 9
    58.               ↑
    59. 1 2 3 4 5 6 7 8 9
    60.               ↑
    61. before swap:1,2,3,4,5,6,7,8,9
    62. after swap:1,2,3,4,5,6,7,8,9
    63. pivot=6, left=5, right=6
    64. 1 2 3 4 5 6 7 8 9
    65.           L R
    66. 1 2 3 4 5 6 7 8 9
    67.           ↑
    68. 1 2 3 4 5 6 7 8 9
    69.           ↑

    归并排序

    归并排序和中国好声音晋级机制

    归并排序非常类似于电视节目中音乐类选秀节目的晋级机制。

    比如，中国好声音，

    • 每个导师会通过盲选得到14名学员
    • 第一轮PK：14名学员进行两两分组，共7组，每组组内学员进行PK，胜出者可以晋级下一轮比赛，第一轮PK结束后，每个导师会得到7强学员，
    • 第二轮PK：7强学员再进行两两分组，而匹配不到对手的学员，直接晋级四强，剩余3组进行组内PK，得出其余三名四强学员。
    • 第三轮PK：4强学员继续两两分组PK，得出二强学员。
    • 第四轮PK：2强学员PK，得出最强学员。

    最后四位导师带着各自的最强学员，进行总决赛。

    当然，上面的晋级机制选拔出来的冠军是赛制公平的，但是亚军、季军、殿军是不公平的。

    为什么这么说呢？

    我们假设给14名学员的实力进行1~14的标记，1代表最弱，14代表最强。

    我们可以发现，冠军14确实是最强的，但是亚军12并非实力使然，而是利用了晋级机制的漏洞。真实实力排名亚军的13，由于运气比较差，在第一轮就遇到了冠军实力的14，所以早早退场。

    因此为了保证公平，一般赛制都会引入复活赛概念。所谓复活赛，即在每轮比赛失败的学员中进行PK，复活出实力较强的失败学员，然后让他们再次挑战已经晋级的学员，将因为运气晋级的学员PK下去。

    但是复活赛机制依旧不是公平的。

    真正公平的赛制是这样的，比如第一轮选拔中，13被14PK下去了，这只能证明13的实力弱于14，并不能证明13的实力弱于第一轮中其他晋级选手，所以为了公平，13可以继续跳转除了14外的所有选手。

    而这就是归并排序。 

    归并排序的原理

    归并排序是基于分治思想设计的排序算法。

    归并排序的分解逻辑是，将无序数组不停的进行平分，每次平分都得到两个子序列，直到平分得到的子序列只有一个元素时，才停止平分。

    如下图，就是归并排序对无序数组的分解过程，原数组为[4,7,2,0,9,6,8,1,3,5]，共10个元素，第一轮分解时，start=0，end=9, mid = (start+end)/2 = 4，则start~mid（0~4）分为一个子序列，mid+1~end（5~9）分为一个子序列。然后利用同样地方式将子序列平分，直到分解出来的子序列只有一个元素无法平分时停止。

    当归并排序某个子序列完成彻底分解后，就可以进行合并操作，而合并操作就是将子序列合并为父序列/原数组的过程，并且合并前，需要对子序列与子序列进行比较排序。

    例如，{4,7}序列分解为4、7后就无法再次分解了，此时我们可以比较4、7，将小的首先放入父序列头部，然后再放其他的。

    按此操作，即最终{4,7}序列内容依旧是{4,7}

    此时{4,7}序列有序了，{2}只有单个元素所以也是有序的，因此可以将它们合并会父序列中。合并前，需要比较排序。

    此时的比较策略是，先将{4,7}序列的最小值和{2}序列的最小值进行比较，小的先放入父序列中。

    由于{4,7}序列是有序的，所以4是该序列的最小值，而{2}序列只有一个元素，所以2就是自身序列的最小值，比较4，2，发现2更小，所以将2放入父序列中，然后{2}序列就没有元素了，换句话说，{4,7}序列没有了比较对象了，因此{4,7}序列整个放入父序列中，因此父序列为{2,4,7}。

    接着，比较0，9，得到有序序列{0,9}

    此时，{2,4,7}有序了，{0,9}有序了，因此可以将它们合并到父序列了。同样地，在合并前，对两个序列进行比较排序，

    • 首先比较两个序列的最小值，即比较{2,4,7}的2，和{0，9}的0，最终0较小，被首先放入父序列中
    • 之后，比较{2,4,7}序列和{9}序列的最小值，即2和9的比较，最终2较小，被放入父序列
    • 之后，比较{4,7}序列和{9}序列的最小值，即4和9的比较，最终4较小，被放入父序列
    • 之后比较{7}序列和{9}序列的最小值，即7和9的比较，最终7较小，被放入父序列
    • 此时{2,4,7}序列的元素全部被放入了父序列，因此{9}序列没有了比较对象，直接放入父序列

    因此父序列元素为{0,2,4,7,9}

    按照上面的方式，同理可得如下

    归并排序的实现

    1. /* JavaScript Node ACM模式 控制台输入获取 */
    2. const readline = require("readline");
    3.  
    4. const rl = readline.createInterface({
    5.   input: process.stdin,
    6.   output: process.stdout,
    7. });
    8.  
    9. rl.on("line", (line) => {
    10.   const arr = line.split(",");
    11.   mergeSort(arr); // 4,7,2,0,9,6,8,1,3,5
    12.   console.log(arr.join(" "));
    13. });
    14.  
    15. /* 归并排序 */
    16. function mergeSort(arr, start = 0, end = arr.length - 1) {
    17.   /* 归并排序分解逻辑 */
    18.   if (start < end) { // 当子序列只有一个元素时，停止分解
    19.     let mid = Math.floor((start + end) / 2);
    20.     mergeSort(arr, start, mid);
    21.     mergeSort(arr, mid + 1, end);
    22.     merge(arr, start, mid, end); //分解到子序列只有一个元素时，或子序列有序时，进行合并
    23.   }
    24. }
    25.  
    26. /* 归并排序合并逻辑 */
    27. function merge(arr, start, mid, end) {
    28.   let tmp = []; // tmp数组作为存储父序列的临时容器
    29.   let i = start; // 游标i，指向有序子序列（start~mid）最小值的位置，初始时，有序子序列（start~mid）最小值的位置在start
    30.   let j = mid + 1; // 游标j，指向有序子序列（mid+1~end）最小值的位置，初始时，有序子序列（mid+1~end）最小值的位置在mid+1
    31.  
    32.   for (let k = start; k <= end; k++) { // for循环的k是tmp数组的索引，我们需要将两个子序列排序后合入父序列中，因此k的循环范围是start~end
    33.     if (i > mid) { // 当游标i已经超出子序列（start~mid）范围，则表示当前子序列元素已经全部加入父序列，因此另一个子序列（mid+1, end）的元素已经没有比较对象，可以直接加入父序列
    34.       tmp[k] = arr[j++];
    35.     } else if (j > end) { // 当游标j已经超出子序列（mid+1~end）范围，则表示当前子序列元素已经全部加入父序列，因此另一个子序列（start, mid）的元素已经没有比较对象，可以直接加入父序列
    36.       tmp[k] = arr[i++];
    37.     } else if (arr[i] < arr[j]) { // 比较两个子序列的最小值，将较小的存入tmp中，然后对应游标位置后移一位，表示之前游标指向的最小值已经合入父序列tmp中，同时tmp的k也随着for循环自增
    38.       tmp[k] = arr[i++];
    39.     } else {
    40.       tmp[k] = arr[j++];
    41.     }
    42.   }
    43.  
    44.   for (let n = start; n <= end; n++) { // 将tmp数组中存储的父序列合入原始数组对应范围
    45.     arr[n] = tmp[n];
    46.   }
    47. }

    归并排序的时间复杂度

    归并排序分解过程不停的将数组进行二分，假设数组元素有n个，则最多要分解logn轮，

     然后每轮合并时比较排序的次数最多是n次，因此归并排序的时间复杂度为O(nlogn)。

    归并排序的非递归实现

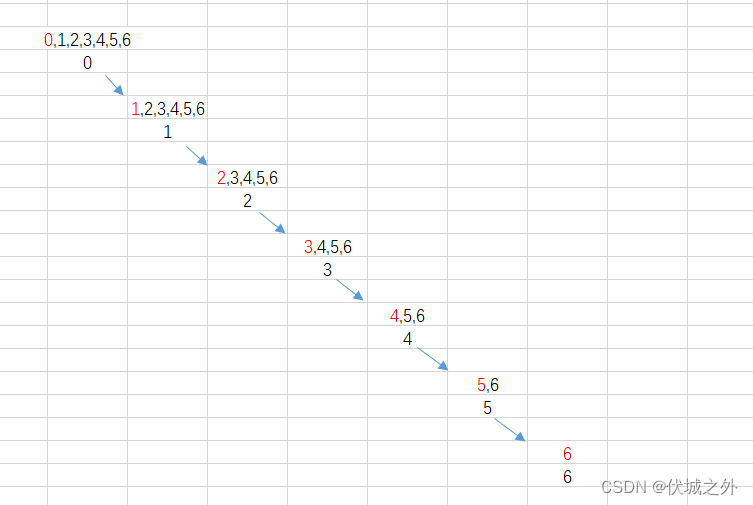
    归并排序的递归实现中，递归仅用于将无序数组不停的平分，直到无序数组被平分至所有子序列都只有一个元素。如下图所示：

    也就是说，递归分解的最终目的是将

    [4,7,2,0,9,6,8,1,3,5] 分解为 {4},{7},{2},{0},{9},{6},{8},{1},{3},{5}

    然后进行合并。

    但是，[4,7,2,0,9,6,8,1,3,5] 分解为 {4},{7},{2},{0},{9},{6},{8},{1},{3},{5} 的工作，并不一定要依赖于递归，通过for循环遍历出每一个数组元素，也能够完成 [4,7,2,0,9,6,8,1,3,5] 分解为 {4},{7},{2},{0},{9},{6},{8},{1},{3},{5} 的工作。并且改用for的话，消耗的内存要比递归函数小很多。

    只是分解后的如何合并成了新的问题？

    采用递归实现的归并排序的合并流程是依赖于分解流程的，也就是说基于递归的合并流程，其实是自顶向下的递归的回溯流程。

    而当前我们不再使用递归来进行分解，而是采用for来进行分解，则合并流程就如下图所示，变成一个单纯的自底向上的流程。

    自底向上的合并流程

    • 第一轮：每两个元素合并为一个有序序列
    • 第二轮：每四个元素（两组有序序列）合并为一个有序序列
    • 第三轮：每八个元素（两组有序序列）合并为一个有序序列
    • ......

    如果原数组一共有n个元素，则需要合并 logn 轮，考虑到 logn 可能不是整数，所以对其进行向上取整。

    因此，实现代码如下：

    1. /* JavaScript Node ACM模式 控制台输入获取 */
    2. const readline = require("readline");
    3.  
    4. const rl = readline.createInterface({
    5.   input: process.stdin,
    6.   output: process.stdout,
    7. });
    8.  
    9. rl.on("line", (line) => {
    10.   let arr = line.split(",");
    11.   arr = arr.map((item) => parseInt(item));
    12.   mergeSort(arr);
    13.   console.log(arr.join(" "));
    14. });
    15.  
    16. function mergeSort(arr) {
    17.   let cycle = Math.ceil(Math.log2(arr.length));
    18.   let count = 0;
    19.  
    20.   while (cycle > 0) {
    21.     let inc = 2 << count;
    22.     for (let i = 0; i < arr.length; i += inc) {
    23.       merge(arr, i, i + inc - 1);
    24.     }
    25.     count++;
    26.     cycle--;
    27.   }
    28.  
    29.   /* for (let i = 0; i < arr.length; i += 2) {
    30.     merge(arr, i, i + 1);
    31.   }
    33.   for (let i = 0; i < arr.length; i += 4) {
    34.     merge(arr, i, i + 3);
    35.   }
    37.   for (let i = 0; i < arr.length; i += 8) {
    38.     merge(arr, i, i + 7);
    39.   }
    41.   for (let i = 0; i < arr.length; i += 16) {
    42.     merge(arr, i, i + 15);
    43.   } */
    44. }
    45.  
    46. function merge(arr, start, end) {
    47.   let mid = Math.floor((start + end) / 2);
    48.  
    49.   let tmp = [];
    50.   let i = start;
    51.   let j = mid + 1;
    52.  
    53.   for (let k = start; k <= end; k++) {
    54.     if (i > mid) {
    55.       tmp[k] = arr[j++];
    56.     } else if (j > end) {
    57.       tmp[k] = arr[i++];
    58.     } else if (arr[i] > arr[j]) {
    59.       tmp[k] = arr[j++];
    60.     } else {
    61.       tmp[k] = arr[i++];
    62.     }
    63.   }
    64.  
    65.   for (let k = start; k <= end; k++) {
    66.     arr[k] = tmp[k];
    67.   }
    68. }
  • 相关阅读:
    十三、MySQL 主从复制
    2022.11.25Dungeon Master POJ - 2251
    基于PRM(probabilistic roadmaps)算法的机器人路线规划算法matlab仿真
    力扣每日一题2022-09-05中等题：寻找重复的子树
    nn.KLDivLoss,nn.CrossEntropyLoss,nn.MSELoss,Focal_Loss
    Docker部署Emqx并配置ssl支持微信小程序
    C++结构型模式-组合模式
    Excel二维码图片生成器
    2_1 计算机组成与体系结构
    LoadBalancer （本地负载均衡）
  • 原文地址：https://blog.csdn.net/qfc_128220/article/details/126120670