CH11：Divide and Conquer：More Algorithms

10.1 Square matrix multiplication 矩阵相乘

10.1.1 分治算法

$A=(a_{ij})，B=(b_{ij})$，都是n×n的矩阵

定义： $C=A\times B,c_{ij}={\sum }_{k=1}^n{a}_{i,k}{b}_{k,j}$

矩阵相乘的算法：

分治：partition

矩阵相乘符合标量乘法

矩阵乘法的分治：Square-Matrix-Multiply-Recursive(A,B)

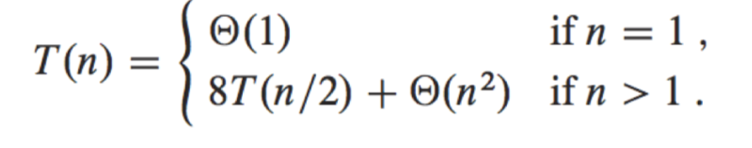
10.1.2 Strassen’s method

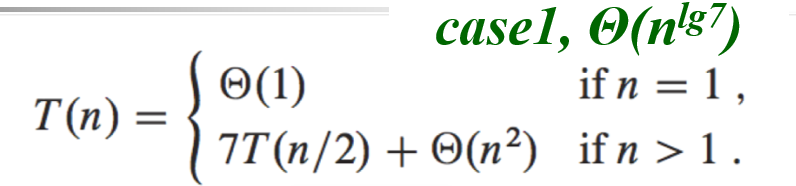
10.2 The Maximum - subarray problem

10.2.1 问题背景

要求最低点买入？最高点卖出？

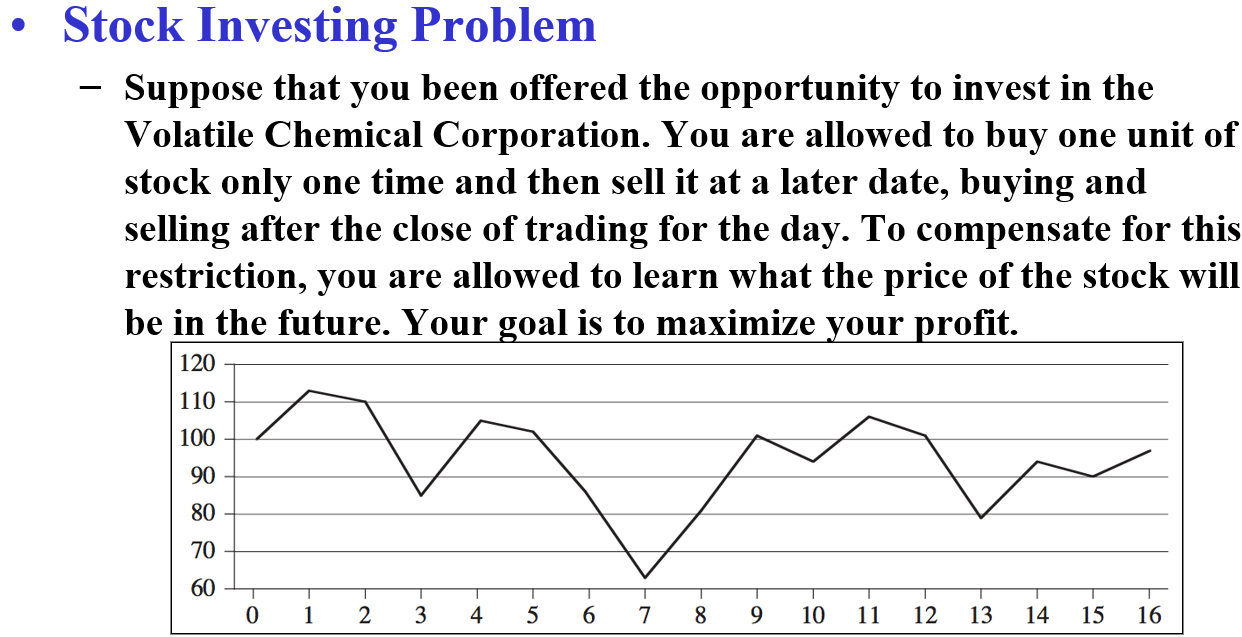
建模为最和子数组和问题：

10.2.2 暴力解法

暴力解法：穷举所有的子数组——穷举所有的下标可能情况，找出最大值的子数组.

暴力解法程序如下：

// 暴力穷举子数组 
int maxSum_brute(vector<int>& vec) {
	int maxSum = -1;
	int besti = -1, bestj = -1;
	for (int i = 0; i < vec.size(); i++) {
		int tempSum = vec[i];
		for (int j = i+1; j < vec.size(); j++) {
			tempSum += vec[j];
			if (tempSum > maxSum) {
				maxSum = tempSum;
				besti = i;
				bestj = j;
			}
		}
	}
	return maxSum;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

时间复杂度是$O(n^2)$

10.2.3 分治法

分治法需要额外考虑一个cross的情况：最优解可能是在两个子数组的中间得到。
{ 二分 n 推 n − 1

{二分n推n−1​

• Divide：把数组分成两个数组
• Conquer：递归求解子问题，并额外求解跨越中间的情况
• Combine：三挑一，找到最大和子数组

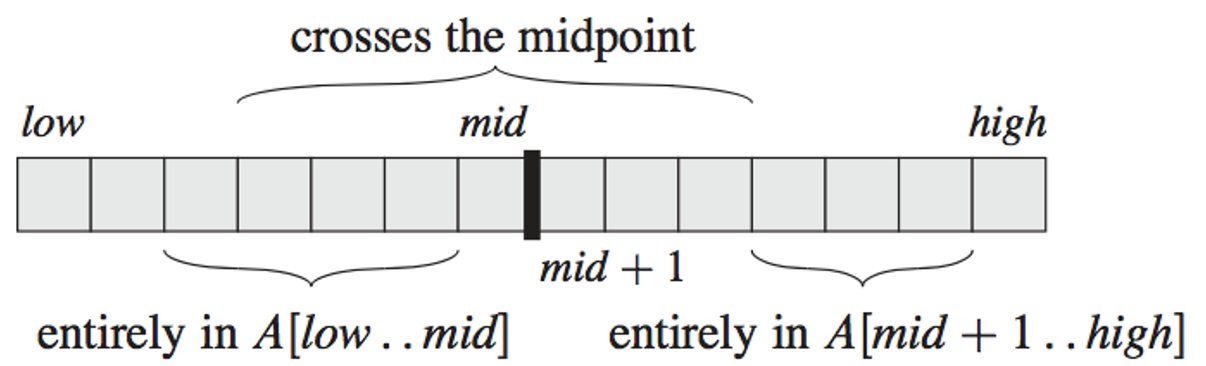
算法实现如下：

// 分治法，含有cross
int getMidMax(vector<int>& vec, int start, int end, int mid) {
	int maxsum = vec[mid];
	int maxNum = vec[mid];
	for (int i = mid - 1; i >= start; i--) {
		maxsum += vec[i];
		if (maxsum > maxNum) {
			maxNum = maxsum;
		} 
	}
	maxsum = maxNum;
	for (int i = mid + 1; i <= end; i++) {
		maxsum += vec[i];
		if (maxsum > maxNum) {
			maxNum = maxsum;
		}
	} 
	return maxNum;
}

int maxSum(vector<int>& vec, int start, int end) {
	if (start == end) 
		return vec[start];
	// 分 
	int mid = (start + end) / 2;
	// 治 
	int maxSumLeft = maxSum(vec, start, mid);
	int maxSumRight = maxSum(vec, mid + 1, end);
	int maxSumCross = getMidMax(vec, start, end, mid);
	// 合并 
	int maxNum = max(maxSumLeft, maxSumRight);
	maxNum = max(maxNum, maxSumCross);
	return maxNum;
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

时间复杂度：$nlgn$

$T(n)=2T(n/2)+\Theta (n)$

$f(n)=n^{lo{g}_2^2}=n=\Theta (nl{g}^{0}k)$