【考研】数据结构考点——直接插入排序

​前言

本文内容源于对《数据结构（C语言版）》（第2版）、王道讲解学习所得心得、笔记整理和总结。

插入排序的三种方法：直接插入排序、折半插入排序和希尔排序。本文内容主要针对直接插入排序，包括了基于顺序表、带头结点单链表和不带头结点单链表的直接插入排序算法。“干货”较足，建议收藏，以防丢失。

可搭配以下链接一起学习：

【考研】数据结构考点——顺序查找_住在阳光的心里的博客-CSDN博客

【考研复习：数据结构】查找（不含代码篇）_住在阳光的心里的博客-CSDN博客

本文已参加活动，其地址：CSDN21天学习挑战赛

一、基本概念

1、插入排序的基本思想：

       每一趟将一个待排序的记录，按其关键字的大小插入到已排好序的一组记录的适当位置上，直到所有待排序记录全部插入为止。

2、直接插入排序（Straight Insertion Sort）的基本操作：

        将一条记录插入到已排好序的有序表中，从而得到一个新的、记录数量增1的有序表（最简单的排序方法）。

3、排序算法效率的评价指标：

（1）执行时间：高效的排序算法的比较次数和移动次数都应该尽可能的少。

（2）辅助空间：理想的空间复杂度为 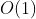 ，即算法执行期间所需要的辅助空间与待排序的数据量无关。

 
二、基于顺序表的直接插入排序

//数据元素类型定义
 
#define MAXSIZE 20    //顺序表的最大长度
typedef int KeyType;   //定义关键字类型为整型
typedef struct{   
    KeyType key;   //关键字项
    InfoType otherinfo;   //其他数据项
}RedType;    //记录类型
 
typedef struct {
    RedType r[MAXSIZE + 1];   // r[0] 闲置或用做哨兵单元
    int length;    //顺序表长度
}SqList;   //顺序表类型

三、算法实现

（一）算法步骤

1、设待排序的记录存放在数组中 r[1...n] 中，r[1] 是一个有序序列。
2.、循环 n - 1 次，每次使用顺序查找法，查找 r[i] (i = 2 ,..., n) 在已排好序的序列 r[1...i-1] 中的插入位置，然后将 r[i] 插人表长为 i - 1 的有序序列 r[1...i-1]，直到将 r[n] 插入表长为 n - 1 的有序序列r[1...n-1] ,最后得到一个表长为 n 的有序序列。

举例：

已知待排序记录的关键字序列为{49, 38, 65, 97, 76, 13, 27, 49}, 请给出用直接插入排序法进行排序的过程。

解：直接插入排序过程下图所示，其中表格底色为黄色为已排好序的记录的关键字。 

在具体实现 r[i] 向前面的有序序列插人时，有两种方法:

（1）将r[i] 与 r[1], r[2]，... , r[i-1] 从前向后顺序比较;

（2）将 r[i] 与 r[i-1], r[i-2]，... , r[1] 从后向前顺序比较。

这里采用（2）方法，和顺序查找类似，为了在查找插入位置的过程中避免数组下标出界，在 r[0] 处设置监视哨，在自 i - 1 起往前查找插入位置的过程中，可以同时后移记录。

（二）算法描述

// 对顺序表 L 做直接插入排序
// 从后往前找
void InsertSort (SqList &L){     
    for(i = 2; i <= L. length; ++i){
        if(L.r[i].key < L.r[i-1].key){        //“<"， 需将 r[i] 插入有序子表
            L.r[0] = L.r[i];       //将待插入的记录暂存到监视哨中
            L.r[i] = L.r[i-1];      //r[i-1] 后移
            for(j = i-2; L.r[0].key < L.r[j].key; --j)     //从后向前寻找插入位置
                L.r[j+1] = L.r[j];       //记录逐个后移，直到找到插入位置
            L.r[j+1] = L.r[0];     //将 r[0] 即原 r[i], 插入到正确位置
        }
    }
}

（三）算法分析

（1）时间复杂度

• 从时间来看，排序的基本操作为：比较两个关键字的大小和移动记录。
• 对于其中的某趟插入排序， 上述算法中内层的 for 循环次数取决于待插记录的关键字与前 i - 1个记录的关键字之间的关系。
• 在最好情况（正序：待排序序列中记录按关键字非递减有序排列）下，比较1次，不移动；
• 在最坏情况（逆序：待排序序列中记录按关键字非递增有序排列下，比较 i 次(依次同前面的 i -1 个记录进行比较，并和哨兵比较 1 次)，移动 i + 1次(前面的 i -1 个记录依次向后移动，另外开始时将待插入的记录移动到监视哨中，最后找到插人位置，又从监视哨中移过去)。
• 对于整个排序过程需执行 n - 1 趟，最好情况下，总的比较次数达最小值 n - 1，记录不需移动；最坏情况下，总的关键字比较次数 KCN 和记录移动次数 RMN 均达到最大值，分别为

若待排序序列中出现各种可能排列的概率相同，则可取上述最好情况和最坏情况的平均情况。在平均情况下，直接插入排序关键字的比较次数和记录移动次数均约为   ，由此，直接插入排序的时间复杂度为O(n)。

（2）空间复杂度
直接插入排序只需要一个记录的辅助空间 r[0]，所以空间复杂度为O(1)。
 

（四）算法特点

（1）稳定排序。
（2）算法简便，且容易实现。
（3）也适用于链式存储结构，只是在单链表上无需移动记录，只需修改相应的指针。
（4）更适合于初始记录基本有序(正序)的情况，当初始记录无序，n 较大时，此算法时间复杂度较高，不宜采用。

四、补充：基于单链表的直接插入排序

建议搭配以下链接来一起学习：
还在写，待补充：区分带头结点与不带头结点的单链表

typedef struct LNode{    //单链表的结构定义
	int data;   //结点的数据域
	struct LNode *next;   //结点的指针域
}LNode, *LinkList;

（一）复习单链表插入操作（带头结点的单链表 ）

【算法步骤】
将值为 e 的新结点插入到表的第 i 个结点的位置上，即插入到结点  与  之间，具体插入过程如上图所示，图中对应的 5 个步骤说明如下。
① 查找结点  并由指针 p 指向该结点。
② 生成一个新结点 *s。
③ 将新结点 *s 的数据域置为 e。
④ 将新结点 *s 的指针域指向结点  。
⑤ 将结点 *p 的指针域指向新结点 *s。

【算法描述】

// 在带头结点的单链表 L 中第 i 个位置插入值为 e 的新结点
Status ListInsert (LinkList &L, int i, ElemType e)
{
    p = L;
    j = 0;
    while(p && (j < i - 1)){    //查找第 i-1 个结点，P指向该结点
        p = p->next;
        ++j;
    }
 
    if(!p || j > i - 1)     // i > n+1 或者 i < 1
        return ERROR;
   
    s = new LNode;    //生成新结点 *s
    s->data = e;    //将结点 *s 的数据域置为 e
 
    s->next = p->next;   //将结点 *s 的指针域指向结点ai
 
 
    p->next = s;   //将结点 *p 的指针域指向结点 *s
    return OK;
}

【算法分析】

和顺序表一样，如果表中有 n 个结点，则插入操作中合法的插入位置有 n + 1 个，即1 ≤ i ≤ n+1。当 i = n + 1时，新结点则插在链表尾部。

在第 i 个结点之前插入一个新结点，必须首先找到第 i - 1 个结点，单链表的插入操作的时间复杂度为O(n)。

（二）带头结点的单链表的直接插入排序 

//单链表的结构定义
typedef struct LNode{    
	int data;   //结点的数据域
	struct LNode *next;   //结点的指针域
}LNode, *LinkList;
 
 
// 带头结点的单链表的直接插入排序
LNode* Insert_Sort(LNode* list)   // list为待排序关键字序列
{
    LNode* cur, *pre, *p;     
    cur = list->next->next;     //指向第二个结点 
    
    //断开第一个与第二个结点之间的链接，此时链表变成头结点+首元结点    
    list->next->next = NULL;
 
    while(cur){
        p = cur->next;      //保存当前结点的下一个结点的指针
        pre = list;     //临时指针pre
        
        //比较结点值大小，找到合适的位置 
        while(pre->next && pre->next->data < cur->data){
            pre = pre->next;
        }
 
        //进行插入操作 
        cur->next = pre->next; 
        pre->next = cur;
        cur = p;
    }
    return list;
}

可参考链接：c语言带头节点的单链表插入排序_ejdjdk的博客-CSDN博客 

（三）不带头结点的单链表的直接插入排序

//单链表的结构定义
typedef struct LNode{    
	int data;   //结点的数据域
	struct LNode *next;   //结点的指针域
}LNode, *LinkList;
 
 
// 不带头结点的单链表的直接插入排序
LNode *Insert_Sort(LNode* list)
{
    LNode *p1 = list, *p2 = p1->next;   //p1所指结点为首元结点，p1和p2为向下移动指针
    LNode *q = NULL;    //q为从头指针移动的指针
    p1->next = NULL;    //从未排序的链表处断开
    p1 = p2;    //p1指向断开后未排序的第一个结点，即p2
    while(p1 != NULL)    //链表不为空，为真
    {
        p2 = p1->next;   //p2指向p1的下一个结点
        q = list;   //q移动到头结点
        if(list->data > p1->data)    //当待排序的数值小于头结点时后为真
        {
            p1->next = list;    //将小于头结点的结点设为头结点
            list = p1;    //头结点重新指向第一个单链表第一个结点
        }
        else{   //当单链表不为空且小于断开链表部分的待插入的前一个结点，
            while(q->next != NULL && q->next->data < p1->data)
                q=q->next;    //向下移动
 
            p1->next = q->next;    //插入结点操作
            q->next = p1;    //插入结点操作
        }
        p1 = p2;   //p1指向p2，即断开的待插入单链表的第一个结点
    }
    return list;
}

可参考链接：无头结点的单链表直接插入排序_xiaochenxiaoren的博客-CSDN博客 

​