矩阵分析与应用 - 码农知识堂

矩阵分析与应用

Kronecker积

Kronecker积是表示矩阵特殊乘积的一种简洁数学符号,也称直积或张量积。一个m*n矩阵A和一个p*q的矩阵B的Kronecker积记作 $A\otimes B$ ，它是一个mp*nq的矩阵。

右Kronecker积定义：m*n矩阵A和p*q的矩阵B的右Kronecker积 $A\otimes B$ 定义为：

$A\otimes B=[a_{ij}B]=\begin{bmatrix} a_{11}B &a_{12}B & .. . & a_{1n}B\\ a_{21}B & a_{22}B & .. .&a_{2n}B \\ .. . & .. . & .. .&.. . \\ a_{m1}B & a_{m1}B & .. .& a_{mn}B \end{bmatrix}$

左Kronecker积定义：m*n矩阵A和p*q的矩阵B的左Kronecker积 $A\otimes B$ 定义为：

$[A\otimes B]_{left}=[Ab_{ij}]=\begin{bmatrix} Ab_{11} &Ab_{12}& .. . & Ab_{1q}\\ Ab_{21} & Ab_{22} & .. .&Ab_{2q} \\ .. . & .. . & .. .&.. . \\ Ab_{p1} & Ab_{p1} & .. .& Ab_{pq} \end{bmatrix}$

左Kronecker积可以写成 $\left [A\otimes B \right ]_{left}$ 或者 $B\otimes A$ 。

若矩阵 $A_{m\times n}=ab^{T}$ ，则：

$vec(ab^{T})=b\otimes a$

定理：令 $A_{m\times p},B_{p\times q},C_{q\times n}$ ，则：

$vec(ABC)=(C^{T}\otimes A)vec(B)$

Kronecker积有以下性质：

1.对于矩阵 $A_{m\times p},B_{p\times q}$ ，一般有:

$A\otimes B\neq B\otimes A$

2.任意矩阵与零矩阵的Kronecker积对于零矩阵，即：

$A\otimes O=O\otimes A=O$

3.若 $\alpha , \beta$ 为常数，则：

$\alpha A \otimes \beta B=\alpha \beta\left ( A \otimes B \right )$

4对于矩阵 $A_{m\times n},B_{n\times k},C_{l\times p},D_{p\times q}$ ，有：

. $AB\otimes CD =(A\otimes C)(B\otimes D)$

5.对于矩阵 $A_{m\times n},B_{p\times q},C_{p\times q}$ ，有：

$A\oplus\left ( B\pm C \right )=A\oplus B\pm A\oplus C$

$\left ( B\pm C \right )\otimes A=B\otimes A\pm C\otimes A$

6.若矩阵A和B分别有广义逆矩阵 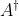$A^{\dagger }$ 和 $B^{\dagger }$ ，则：

$(A\otimes B)^{{\dagger }}=A^{{\dagger }}\otimes B^{{\dagger }}$

若A,B均为可逆的正方矩阵，则：

$\left (A\otimes B \right )^{-1}=A^{-1}\otimes B^{-1}$

7.对于矩阵 $A_{m\times n},B_{p\times q}$ ，有

$\left (A\otimes B \right )^{T}=A^{T}\otimes B^{T}$

$\left (A\otimes B \right )^{H}=A^{H}\otimes B^{H}$

8.对于矩阵 $A_{m\times n},B_{p\times q}$ ，有 $A_{m\times n},B_{p\times q},C_{n\times r},D_{q\times s}$

$rank(A\otimes B)=rank(A)rank(B)$

9.若A是m*m矩阵，B是n*n矩阵，则：

$det(A\otimes B)=(det(A))^{n}(det(B))^{m}$

10.若A是m*m矩阵，B是n*n矩阵，则：

$tr(A\otimes B)=tr(A)tr(B)$

11.对于矩阵 $A_{m\times n},B_{m\times n},C_{p\times q},D_{p\times q}$ ，有

$\left (A+B \right )\otimes \left (C+D \right )=A\otimes C+A\otimes D+B\otimes C+B\otimes D$

$\left [ \sum_{i=1}^{M} A(i)\right ]\otimes \left [ \sum_{j=1}^{N} B(j)\right ]= \sum_{i=1}^{M} \sum_{j=1}^{N}[A(i)\otimes B(j)]$

12.对于矩阵 $A_{m\times n},B_{k\times l},C_{p\times q},D_{r\times s}$ ，有：

$\left (A\otimes B \right )\otimes \left (C\otimes D \right )=A\otimes B\otimes C\otimes D$

13.若 $\alpha _{i}$ 是矩阵A与特征值 $\lambda _{i}$ 对应的特征向量， $\beta _{i}$ 是矩阵B与特征值 $\mu _{i}$ 对应的特征向量，则 $\alpha_{i}\otimes \beta _{i}$ 是矩阵 $A\otimes B$ 与特征值 $\lambda_{i} \mu _{i}$ 对应的特征向量，也是与特征值 $\lambda_{i}+ \mu _{i}$ 对应的特征向量。

14.对于矩阵 $A_{m\times n},B_{p\times q},C_{k\times l}$ ，有：

$\left (A\otimes B \right )\otimes C=A\otimes \left (B\otimes C \right )$

15.对于矩阵 $A_{m\times n},B_{p\times q},C_{n\times r},D_{q\times s}$ ，有：

$\left (A\otimes B \right )\left (C\otimes D \right )=AC\otimes BD$

16.对于矩阵 $A_{m\times n},B_{p\times q}$ ，有：

$exp(A\otimes B)=exp(A)\otimes exp(B)$

广义Kronecker积：给定N个m*r矩阵 $A_{i},i=1,2,.. .,N$ ，它们组成矩阵组 $\left \{ A \right \}_{N}$ 。该矩阵组与N*l矩阵B的Kronecker积称为广义Kronecker积，定义为：

$\left \{ A \right \}_{N}\otimes B=\begin{bmatrix} A _{1}\otimes b_{1}\\ A _{2}\otimes b_{2}\\ .. .\\ A _{N}\otimes b_{N} \end{bmatrix}$

式中， $b_{i}$ 是矩阵B的第i个行向量

与两个矩阵的Kronecker积不同，广义Kronecker积是多个矩阵组成的矩阵组与另一个矩阵的Kronecker积。

设：

$\left \{ A \right \}_{2}=\begin{Bmatrix} \begin{bmatrix} 1&1\\ 2&-1 \end{bmatrix}\\ \begin{bmatrix} 2 &-j\\ 1&j \end{bmatrix} \end{Bmatrix},B=\begin{bmatrix} 1 &2 \\ 1& -1 \end{bmatrix}$

则广义Kronecker积为：

$\left \{ A \right \}_{2}=\begin{Bmatrix} \begin{bmatrix} 1&1\\ 2&-1 \end{bmatrix}\otimes \begin{bmatrix} 1 &2 \end{bmatrix} \\ \begin{bmatrix} 2 &-j\\ 1&j \end{bmatrix} \otimes \begin{bmatrix} 1& -1 \end{bmatrix}\end{Bmatrix}=\begin{bmatrix} 1&1 &2 &2 \\ 2 & -1& 4& -2\\ 2 &-j &-2 &j \\ 1 & j& -1& -j \end{bmatrix}$

广义Kronecker积的性质：

1.若 $\left \{ A \right \}$ 的每一个矩阵为 $m_{1}\times n_{1}$ 矩阵， $\left \{ B \right \}$ 的每一个矩阵为 $m_{2}\times n_{2}$ 矩阵，并且 $\left \{ C\right \}$ 的每一个矩阵为 $m_{3}\times n_{3}$ 矩阵，则：

$\left ( \left \{ A \right \}\otimes \left \{ B \right \}\right )\otimes \left \{ C \right \}= \left \{ A \right \}\otimes \left ( \left \{ B \right \}\otimes \left \{ C \right \} \right )$

2.广义Kronecker积与矩阵直和之间存在以下关系：

$\left \{ A \right \}_{N}\otimes I_{N}=\bigoplus _{i=1}^{N}A_{i}$
相关阅读:
The 2019 ICPC Asia Nanjing Regional Contest J.Spy
MySQL备份与恢复
 Python武器库开发-基础篇(二)
数据结构第四课 -----线性表之队列
 LeetCode_原地哈希_中等_442.数组中重复的数据
 07 SpringMVC 拦截器
 NDP 协议介绍
 JVM系列——jvm常用指令，问题排查
 redis
机器学习-4
原文地址：https://blog.csdn.net/weixin_46007132/article/details/126118926