-
矩阵分析与应用-15-逆矩阵
逆矩阵的定义与性质
一个n xn矩阵称为非奇异矩阵,若它具有n个线性无关的列向量和n个线性无关的行向量。非奇异矩阵也可以从线性系统的观点出发定义:一线性变换或正方矩阵A称为非奇异的。也就是说若它只对零输入产生零输出。否则,它是奇异的。如果一个矩阵非奇异,那么它必定存在逆矩阵。反之,一奇异矩阵肯定不存在逆矩阵。一个n x n 的正方矩阵B满足
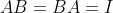 时,就称矩阵B是矩阵A的逆矩阵,记为
时,就称矩阵B是矩阵A的逆矩阵,记为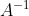 。
。若一个正方矩阵A的所有元素
 分别由它们的余子式
分别由它们的余子式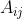 ,代替,然后转置,所得到的矩阵称为A的伴随矩阵,记作 adj(A),
,代替,然后转置,所得到的矩阵称为A的伴随矩阵,记作 adj(A),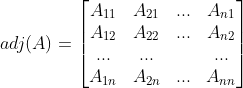
若行列式det(A)≠0,则矩阵A的逆矩阵
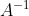 存在,并且唯一。逆矩阵
存在,并且唯一。逆矩阵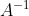 由下式给出:
由下式给出:
例:


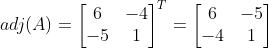
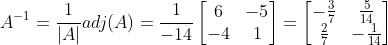
伴随矩阵具有下面的性质
矩阵
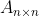 的伴随矩阵 adj(A)的转置等于A的转置的伴随矩阵,即有[
的伴随矩阵 adj(A)的转置等于A的转置的伴随矩阵,即有[![[adj(A)]^T=adj(A^T)](https://1000bd.com/contentImg/2022/08/09/101303393.gif) 。
。若矩阵A 的逆矩阵存在,则称矩阵A是非奇异的或可逆的。关于矩阵的非奇异性或可逆性,下列叙述等价。
(1)A非奇异;
(2)
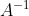 存在;
存在;(3) rank(A) =n;
(4)A的行线性无关;
(5)A 的列线性无关;
(6) det(A)≠ 0;
(7)A的值域的维数是n;
(8)A的零空间的维数是0;
(9)
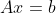 对每一个
对每一个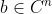 都是一致方程;
都是一致方程;(10)
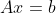 对每一个b有唯一的解;
对每一个b有唯一的解;(11)
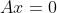 只有平凡解
只有平凡解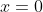 .
.n ×n 矩阵A 的逆矩阵A—1具有以下性质
n ×n 矩阵A 的逆矩阵
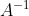 具有以下性质
具有以下性质(1)
 。
。(2)
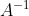 是唯一的。
是唯一的。(3)逆矩阵的行列式等于原矩阵行列式的倒数,即
 。
。(4)逆矩阵是非奇异的。
(5)
 。
。(6)复共瓴转置矩阵
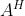 的逆矩阵等于逆矩阵
的逆矩阵等于逆矩阵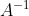 的复共辄转置,即
的复共辄转置,即 。逆矩阵的复共辄转置常采用符号
。逆矩阵的复共辄转置常采用符号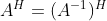 。
。(7)若
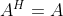 ,则
,则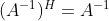 。
。(8)
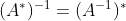 。
。(9)如果A和B都是可逆的,则
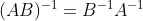
更一般地,有
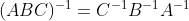
(10)若A = diag(
 )为对角矩阵,则其逆矩阵
)为对角矩阵,则其逆矩阵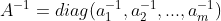
(11)若A非奇异,则
A为正交矩阵
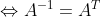
A为酉矩阵
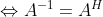
矩阵求逆引理
Sherman-Morrison 公式:令A是一个n× n的可逆矩阵,并且 x和y是两个n × 1向量,使得
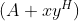 可逆,则
可逆,则
矩阵求逆引理可以推广为矩阵之和l的求逆公式

或
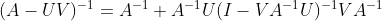
下面是分块矩阵的几种求逆公式。
(1)矩阵A可逆时,为
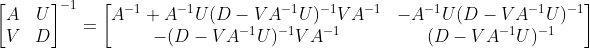
(2)矩阵A和D可逆时,为

(3)矩阵A和D可逆时,为
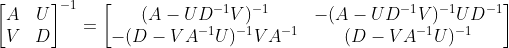
或

-
相关阅读:
硬件及接口学习总结
生产环境TiDB集群缩容TiKV操作步骤
SpringBoot bbs (二) 抓取标签<img>并且打包
docker基础
python html转为为PDF
Hi,你有一份Code Review攻略待查收
【基本数据结构】平衡二叉树
.NET Core 实现后台任务(定时任务)Longbow.Tasks 组件(三)
【附源码】计算机毕业设计SSM时事新闻管理系统
【学习总结】SpringBoot中使用单例模式+ScheduledExecutorService实现异步多线程任务(若依源码学习)
- 原文地址:https://blog.csdn.net/Xiao__fly/article/details/126145326