LeetCode

一、LeetCode - 102. 二叉树的层序遍历

首先，层序遍历表明，是一层一层来存放，并且是从上到下一层一层遍历【我们可以使用队列的结构来存放（类比“遍历文件夹”）】

1 创建queue，根据链表中的size来判断poll的次数

每次记录queue的size，表明队列中还有几个元素，然后挨个弹出node，并且在弹出的过程中，判断node的左子树与右子树是否为null，如果不为null，添加进queue（相当于进行深层次遍历）

int size = queue.size();
ArrayList<Integer> list = new ArrayList<>();
while(size > 0){
    TreeNode node = queue.poll();
    list.add(node.val);
    if(node.left != null){
        queue.add(node.left);
    }
    if(node.right != null){
        queue.add(node.right);
    }
    size--;
}
res.add(list);
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2 全代码

class Solution {
    private List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        if(root == null) return res;
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            ArrayList<Integer> list = new ArrayList<>();
            while(size > 0){
                TreeNode node = queue.poll();
                list.add(node.val);
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
                size--;
            }
            res.add(list);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

拓展：如果该题目没有要求用List的话，可以使用数组来代替（速度会更快）

 // while(!queue.isEmpty()){
 //     int size = queue.size();
 //     int[] list = new int[size];
 //     for(int i = 0; i <= size; ++i){
 //         TreeNode node = queue.poll();
 //         list[i] = node.val;
 //         if(node.left != null){
 //             queue.add(node.left);
 //         }
 //         if(node.right != null){
 //             queue.add(node.right);
 //         }
 //     }
 //     res.add(list);
 // }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

二、LeetCode - 110. 平衡二叉树

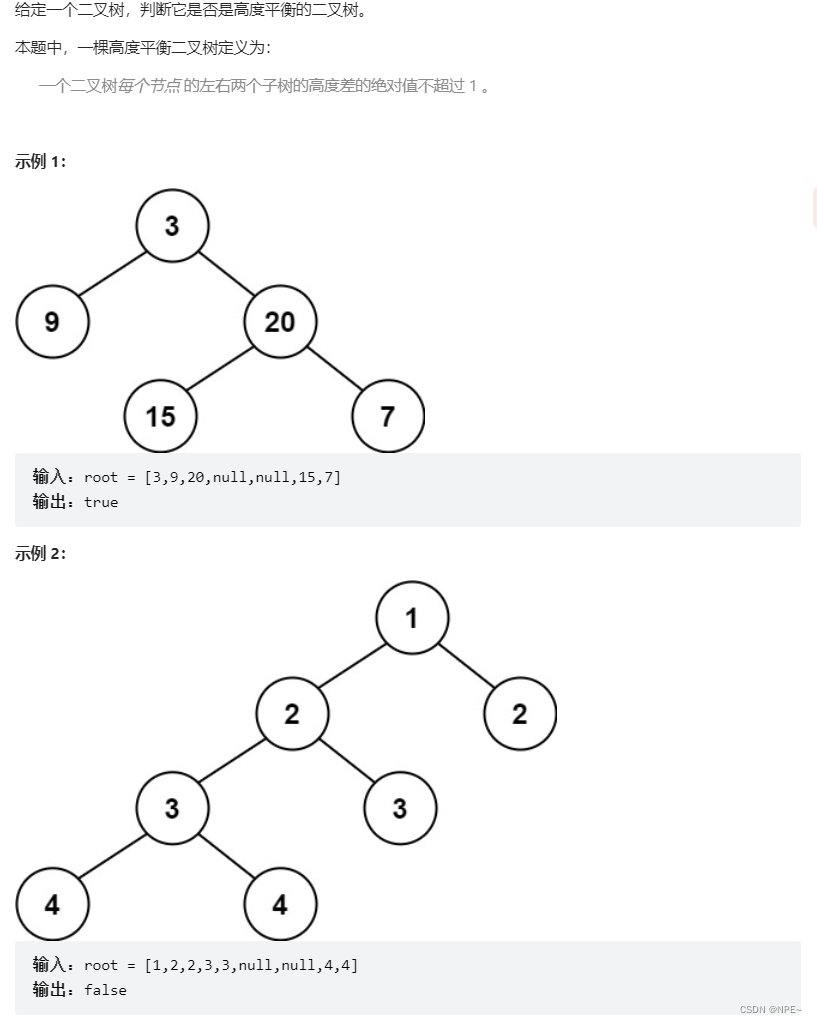
平衡二叉树：叶子节点的高度差不超过1；
因此，我们只需要构造函数，记录以该节点为根节点，判断是否是平衡二叉树，同时，记录下该节点高度，最后判断两叶子节点高度差是否不超过1

1 定义内部类，用于存储高度及该节点信息

class Info{
	public boolean isBalanced;
	public int height;
	
	public Info(boolean isBalanced, int height){
		this.isBalanced = isBalanced;
		this.height = height;
	}
}
1
2
3
4
5
6
7
8
9

2 定义递归函数，用于判断是否是二叉平衡树

public Info process(TreeNode node){
	//如果当前节点为null，默认该节点为平衡的，且高度为0
    if(node == null){
        return new Info(true, 0);
    }
    //当前节点的左子树信息
    Info leftInfo = process(node.left);
    //当前节点的右子树信息
    Info rightInfo = process(node.right);
    //当前节点的高度信息：左右子树的最大高度 + 自身高度1
    int height = Math.max(leftInfo.height, rightInfo.height) + 1;
    //当前节点的isBalanced信息，取决于：左右子树是否平衡，同时左右子树的高度差是否小于2
    boolean isBalanced = leftInfo.isBalanced && rightInfo.isBalanced && 
        Math.abs(leftInfo.height - rightInfo.height) < 2;
     //构建当前节点node信息
    return new Info(isBalanced, height);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

3 全部代码

class Solution {
    public boolean isBalanced(TreeNode root) {
        return process(root).isBalanced;
        
    }
    class Info{
        public boolean isBalanced;
        public int height;
        
        public Info(boolean isBalanced, int height){
            this.isBalanced = isBalanced;
            this.height = height;
        }
    }
    
    public Info process(TreeNode node){
        if(node == null){
            return new Info(true, 0);
        }
        Info leftInfo = process(node.left);
        Info rightInfo = process(node.right);
        int height = Math.max(leftInfo.height, rightInfo.height) + 1;
        boolean isBalanced = leftInfo.isBalanced && rightInfo.isBalanced && 
            Math.abs(leftInfo.height - rightInfo.height) < 2;
        return new Info(isBalanced, height);
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

三、LeetCode - 098. 验证二叉搜索树

二插搜索树：根节点root的左节点的值小于根，右节点的值大于根
leftNode.val < root.val < rightNode.val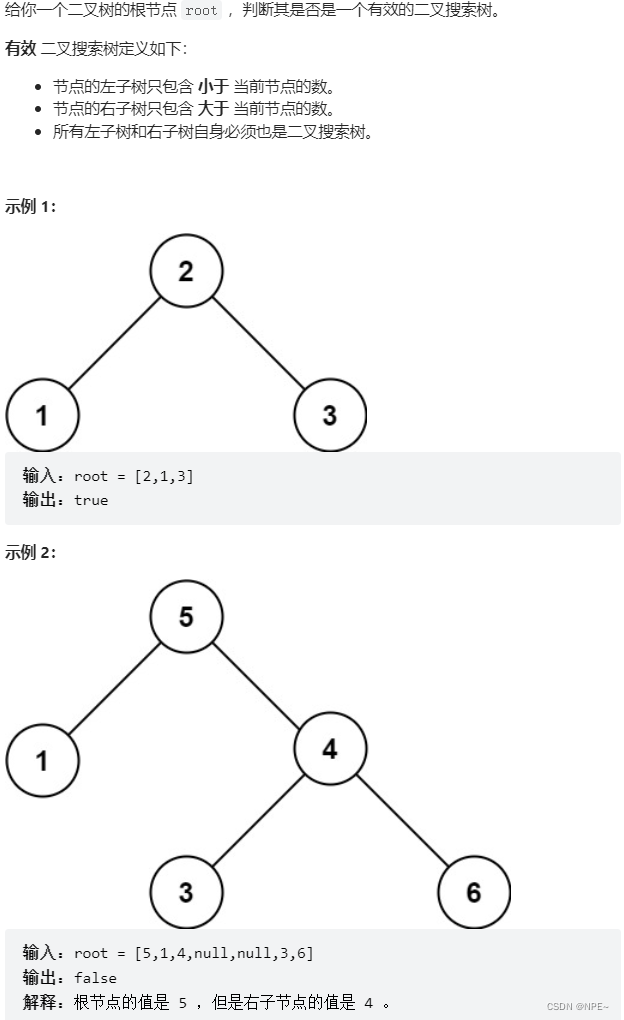

1 定义内部类Info存储子树的最大值，最小值，以及当前节点信息

public Info(boolean isBST, int min, int max){
	   this.isBST = isBST;
	   this.min = min;
	   this.max = max;
}
1
2
3
4
5

2 定义递归方法process，用于处理节点信息

public Info process(TreeNode node){
    if(node == null){
        //此处不能创建空的Info信息返回，因为如果创建空的返回，int默认是0，但是节点的值有可能是负数，会影响判断
        return null;
    }
    Info leftInfo = process(node.left);
    Info rightInfo = process(node.right);
    int max = node.val;
    int min = node.val;
    //每次更新当前节点及其子节点的最大值与最小值
    if(leftInfo != null){
        max = Math.max(leftInfo.max, max);
        min = Math.min(leftInfo.min, min);
    }
    if(rightInfo != null){
        max = Math.max(rightInfo.max, max);
        min = Math.min(rightInfo.min, min);
    }
    boolean isBST = true;
    //当前左节点信息不为null，且不是搜索树
    if(leftInfo != null && !leftInfo.isBST){
        isBST = false;
    }
    if(rightInfo != null && !rightInfo.isBST){
        isBST = false;
    }
    //判断左子树的最大值是否小于root的最小值
    boolean leftMaxLessNode = leftInfo == null ? true : (leftInfo.max < node.val);
    boolean rightMinMoreNode = rightInfo == null ? true : (rightInfo.min > node.val);
    if(!leftMaxLessNode || !rightMinMoreNode){
        isBST = false;
    }
    return new Info(isBST, min, max);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

3 全部代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        return process(root).isBST;
    }
    class Info{
        public boolean isBST;
        public int min;
        public int max;
        
        public Info(boolean isBST, int min, int max){
            this.isBST = isBST;
            this.min = min;
            this.max = max;
        }
    }
    public Info process(TreeNode node){
            if(node == null){
                //此处不能创建空的Info信息返回，因为如果创建空的返回，int默认是0，但是节点的值有可能是负数，会影响判断
                return null;
            }
            Info leftInfo = process(node.left);
            Info rightInfo = process(node.right);
            int max = node.val;
            int min = node.val;
            //每次更新当前节点及其子节点的最大值与最小值
            if(leftInfo != null){
                max = Math.max(leftInfo.max, max);
                min = Math.min(leftInfo.min, min);
            }
            if(rightInfo != null){
                max = Math.max(rightInfo.max, max);
                min = Math.min(rightInfo.min, min);
            }
            boolean isBST = true;
            //当前左节点信息不为null，且不是搜索树
            if(leftInfo != null && !leftInfo.isBST){
                isBST = false;
            }
            if(rightInfo != null && !rightInfo.isBST){
                isBST = false;
            }
            //判断左子树的最大值是否小于root的最小值
            boolean leftMaxLessNode = leftInfo == null ? true : (leftInfo.max < node.val);
            boolean rightMinMoreNode = rightInfo == null ? true : (rightInfo.min > node.val);
            if(!leftMaxLessNode || !rightMinMoreNode){
                isBST = false;
            }
            return new Info(isBST, min, max);
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65