-
四元数简要理解(主要针对计算机图形学)
1.a+bi,a被称为实部,b被称为虚部
2.a+bi->(a,b) 用有序数对来表示
(a,b)=(a,0)+(b,0)
(a,0)+(b,0) = a(1,0)+b(0,1)
那么只需要证明
(1,0) = 1 (0,1)=i
首先证明(1,0)=1
(1,0)(1,0)=(1,0)等同
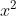 =x 求得x=1,也就证明了(1,0)等同于自然数1
=x 求得x=1,也就证明了(1,0)等同于自然数1(0,1)(0,1)=(-1,0)等同
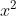 =-1因为只有
=-1因为只有 = -1,所以(0,1)等同于
= -1,所以(0,1)等同于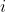
经此证明 复数可以用对数序列来表示
3.a+bi->
 用矩阵来表示
用矩阵来表示这个理解起来就略显生涩,这里大概说一下基本的思想
①C = a
 +b
+b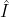 注释 C:矩阵
注释 C:矩阵  :代表1的矩阵
:代表1的矩阵 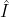 代表
代表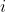 的矩阵。
的矩阵。像有序对表示复数一样,我们需要找到能够代表1的矩阵和代表
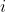 的矩阵
的矩阵②.a*1=a 1的矩阵就意味着什么都不做可以使用
 单位阵
单位阵③1很好理解一个数乘以1代表什么都不干,用方阵就可以表示。
那
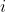 怎么办呢,这就不得不提i的一个特性就是乘以
怎么办呢,这就不得不提i的一个特性就是乘以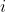 等同于旋转90度
等同于旋转90度也就是
 ,这里就有点生硬了,因为这部分知识需要用到复平面的知识,在后面会有介绍
,这里就有点生硬了,因为这部分知识需要用到复平面的知识,在后面会有介绍④经过2和3我们可以得到

还需要注意一点就是这里用的是列矩阵
4.复平面:x坐标作为实部,y坐标作为虚部,xy构成的二维平面就是复平面
欧拉公式
 ,实部作为横坐标,虚部作为纵坐标,则再二维平面构成了一个圆
,实部作为横坐标,虚部作为纵坐标,则再二维平面构成了一个圆当
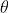 =
= 时得到
时得到
同理还可推得
 = 0.207879.............
= 0.207879.............极坐标表示法


第一象限

第二象限

第三象限

1):初识旋转(a+bi)i = -b + ai相当于旋转90,回想刚才的欧拉公式

2):二维平面假设(x,y)绕原点旋转
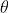 度,
度, 作为旋转公式
作为旋转公式
了解矩阵旋转的应该知道二维旋转矩阵是
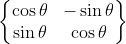 ,可以验证上面的方法是正确的,这里需要回想一下复数的矩阵表示法(这里这么严格的证明都是为了让一切都说的通)
,可以验证上面的方法是正确的,这里需要回想一下复数的矩阵表示法(这里这么严格的证明都是为了让一切都说的通)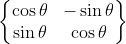


3).三维空间的复数应该怎么写呢,
1) 爱尔兰著名数学家哈密顿初版的想法是既然二维空间是a+bi,那么三维的应该a+bi+cj
那两个四元数相乘

这里的
 无法解决,这个难题困扰了哈密顿10多年,直到十年之后,哈密顿和夫人在小河边溜达,突然灵光乍现想到了现在的四元数
无法解决,这个难题困扰了哈密顿10多年,直到十年之后,哈密顿和夫人在小河边溜达,突然灵光乍现想到了现在的四元数 ,英文名quaternion,哈密顿成四元数的实部为scalar虚部为vector
,英文名quaternion,哈密顿成四元数的实部为scalar虚部为vector 四元数相乘
![q_aq_b=[s_a,a][s_b,b]=[s_as_b - a\cdot b,s_ab+s_ba+a\bigotimes b]](https://1000bd.com/contentImg/2022/08/09/023639505.gif)
纯虚函数
 自己可以验证纯四元数相乘并不是纯四元数,这个结论感觉更重要
自己可以验证纯四元数相乘并不是纯四元数,这个结论感觉更重要单位四元数
![\check{q}=[0,\check{v}]](https://1000bd.com/contentImg/2022/08/09/023641721.gif)

共轭四元数
![q= [s,v] \:\:q^{*}=[s,-v]](https://1000bd.com/contentImg/2022/08/09/023643774.gif) 推理可得
推理可得标准化四元数
![q=[s,v] \:\:\: q{}'=\frac{q}{\sqrt{s^2+v^2}}](https://1000bd.com/contentImg/2022/08/09/023645155.gif)
单位四元数相乘的结果摸为1

![q_a=[s_a,a] \: q_b=[s_b,b] \\ {|q_aq_b|}^2=s_a^2(s_b^2+b^2)+a^2(s_b^2+b^2)=(s_a^2+a^2)(s_b^2+b^2)=|q_a|^2|q_b|^2](https://1000bd.com/contentImg/2022/08/09/023647102.gif) (个人觉得这个推理过程比最后的结论要精彩的多)
(个人觉得这个推理过程比最后的结论要精彩的多)根据余弦定理(
 )
)根据上图可得
![q_c = [s_c,c]=[s_a,a][s_b,b]=[s_as_b-a\bigodot b,s_ab+s_ba+a\otimes b] \\d^2 = s_b^2a^2 + s_a^2b^2 -2s_bas_abcos(\pi-\theta ) \\ =s_b^2a^2 + s_a^2b^2+2s_bas_abcos\theta\\ c^2=d^2+a^2b^2sin^2\theta\\= s_b^2a^2 + s_a^2b^2+2s_bas_abcos\theta+a^2b^2sin^2\theta\\](https://1000bd.com/contentImg/2022/08/09/023649197.gif)


逆四元数证明过程

4.经过一系列的铺垫,我们终于要琢磨怎么才能用四元数进行旋转呢
假设旋转轴为

旋转角度为
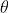
被旋转点为p(这里有一个隐形前提就是旋转轴是穿过原点的)
则旋转四元数为q=
![[cos\theta,sin \theta \hat{v}\]](https://1000bd.com/contentImg/2022/08/09/023655181.gif) ,被旋转点
,被旋转点![[0,p]](https://1000bd.com/contentImg/2022/08/09/023655976.gif) (向量也行,因为我们暂时只考虑穿过原点)
(向量也行,因为我们暂时只考虑穿过原点)1)假设p和旋转轴(
 ),垂直,
),垂直,![[cos \theta , sin \theta \hat v][0,p]=[0,cos \theta p+sin \theta \hat v \bigotimes p]](https://1000bd.com/contentImg/2022/08/09/023657782.gif) (推理过程可得知,只要旋转轴和待旋转向量垂直,就不会生四元数缩放,也就是实部为0)
(推理过程可得知,只要旋转轴和待旋转向量垂直,就不会生四元数缩放,也就是实部为0)这里我们假设旋转角度为90,p为(1,0,0)旋转轴为(0,1,0)带入上面进行验证结果为[0,-k],证明是正确的
2).如果p和旋转轴(
 )不垂直我们会得到
)不垂直我们会得到 ![[cos \theta , sin \theta \hat v][0,p]=[-sin\theta \hat v\cdot p,cos \theta p+sin \theta \hat v \bigotimes p]](https://1000bd.com/contentImg/2022/08/09/023658579.gif) 可以看到这里实部不为0(也就是产生了缩放)
可以看到这里实部不为0(也就是产生了缩放)然后一个奇葩的四元数旋转就产生了
![q=[s,\lambda \hat v] \:\:\:s^2+\lambda^2=1](https://1000bd.com/contentImg/2022/08/09/023659610.gif) (因为q是单位四元数)
(因为q是单位四元数)![p=[0,p]](https://1000bd.com/contentImg/2022/08/09/023700642.gif)
![q^{-1}=[s,-\lambda \hat v]](https://1000bd.com/contentImg/2022/08/09/023701439.gif) //因为q是单位四元数所以
//因为q是单位四元数所以
 =
=![[s,\lambda \hat v][0,p][s,-\lambda \hat v]](https://1000bd.com/contentImg/2022/08/09/023704315.gif) =
=带入s=cos
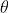
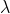 =sin
=sin
![qpq^{-1}=[0,(1-cos2\theta)(\hat v\cdot p)\hat v+cos2\theta p+sin2\theta\hat v\otimes p]](https://1000bd.com/contentImg/2022/08/09/023709583.gif) (不知道怎么来的 可以看看三角函数尝试自己推导一下)
(不知道怎么来的 可以看看三角函数尝试自己推导一下)依据这个公式
我们假设旋转轴为(0,0,i)旋转变量为(i,0,0)旋转角度为90
则s=0

![\hat v =[0,0,1] p=[1,0,0]](https://1000bd.com/contentImg/2022/08/09/023712286.gif) 带入上面的公式
带入上面的公式 [0,-p]也就是[1,0,0]旋转之后变为[-1,0,0]实际却旋转了180度,比我们想要的多了一倍,然后就是著名的半角(half-angle)旋转
[0,-p]也就是[1,0,0]旋转之后变为[-1,0,0]实际却旋转了180度,比我们想要的多了一倍,然后就是著名的半角(half-angle)旋转如果我们将要旋转的角度除以2带入公式则
![qpq^{-1}=[0,(1-cos\theta)(\hat v\cdot p)\hat v+cos\theta p+sin\theta\hat v\otimes p]](https://1000bd.com/contentImg/2022/08/09/023714630.gif)
还是以转轴为(0,0,i)旋转变量为(i,0,0)旋转角度为90距离我们的到
 [0,[0,1,0]]此时符合结论,当然这个例子是比较简单的,但是我也不想过于复杂的去证明,觉得没啥必要,了解一点点帮助理解和记忆,我觉得对于图形学中的四元数旋转就足够了,这里同样没有解释为什么就想到了来通过
[0,[0,1,0]]此时符合结论,当然这个例子是比较简单的,但是我也不想过于复杂的去证明,觉得没啥必要,了解一点点帮助理解和记忆,我觉得对于图形学中的四元数旋转就足够了,这里同样没有解释为什么就想到了来通过 来完成旋转,感兴趣的小伙伴可以自己去看看,我这里碍于自己能力和时间成本的原因就不再多解释了
来完成旋转,感兴趣的小伙伴可以自己去看看,我这里碍于自己能力和时间成本的原因就不再多解释了5.复数的矩阵形式和简写



根据结合律

那么我们回忆一下
四元数旋转公式
 ,那么可以看到原来需要两步计算的 现在可以一步完成
,那么可以看到原来需要两步计算的 现在可以一步完成


-
相关阅读:
Redis缓存设计与性能优化
PostgreSQL基础入门
X11协议基础与实践
锂热电池检测设备 你一定没见过这种检测方式!
【Java】泛型通配符
C++继承出现class不明确的解决办法
第四章 流程编排
最新基于R语言lavaan结构方程模型(SEM)技术
详细安装node.js管理工具nvm,以及对应版本的npm(npm6.x)过程中遇到的问题
Kubernetes新增节点
- 原文地址:https://blog.csdn.net/panzhijiepanzhiyang/article/details/125760914