---

直接插入排序算法的时间复杂度为O(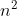),如果待排序的序列为"正序"时，时间复杂度为O(n)，但是如果比较大的数字在第一个位置，那么进行排序的话需要一直移动到最后一位，比较适合基本有序的排序和数据量不大的排序。希尔排序基于这两点分析对直接插入排序进行改进

---

目录

一、排序过程

二、代码

三、性能及稳定性分析

1.空间复杂度

2.时间复杂度

3.稳定性

---

一、排序过程

先将待排序的序列表分割成若干形如L[i,i+d,i+2d,...,i+kd]的“特殊”子表，即把相隔某个“增量”的记录组成一个子表，对每个子表进行直接插入排序，当执行到表中的元素基本有序的时候，在对全体元素进行一次直接插入排序。

固定增量的计算为d=n/2,，并且最后一个增量为1。

推荐一个关于数据结构的网站里面有很多知识，排序、堆栈、索引等。数据结构

示意图：（后面几轮和前面几轮思想一样，所以速度加快了）

二、代码

package sort;
 
/**
 * @author The丶Alanx
 */
public class ShellSort {
    public static void main(String[] args) {
        int[] arr = {3, 6, 4, 1, 9, 6, 5, 8, 7, 2};
        System.out.println("排序前为：");
        for (int i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
        shellsort(arr, arr.length);
        System.out.println("排序后为：");
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }
 
    public static void shellsort(int[] arr, int n) {
        int temp = 0;
        for (int dk = n / 2; dk >= 1; dk = dk / 2) {    //步长变化
            for (int i = dk; i < n; i++) {
                if (arr[i] < arr[i - dk]) {             //将arr[i]插入有序增量子表
                    temp = arr[i];                          //中间变量存放在temp
                    for (int j = i - dk; j >= 0 && temp < arr[j]; j -= dk) {
                        arr[j + dk] = arr[j];               //记录后移，查找插入的位置
                        arr[j] = temp;             //插入
                    }
                }
            }
        }
    }
}

第一趟排序过程： 

结果：

  

三、性能及稳定性分析

1.空间复杂度

因为排序的整个过程中，仅在当前的数组中操作，没有使用另一个空数组，仅使用了常熟个辅助单元，因此时间复杂度为O(1)。

2.时间复杂度

因为希尔排序的时间复杂度和增量序列函数有关系，所以当n在某个特定范围内，希尔排序的时间复杂度约为O(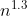),在最坏情况下希尔排序的时间复杂度为O()

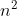3.稳定性

由上上图对希尔排序第一趟的分析，黑色的6开始在前面蓝色的6在后面，而排完序后黑色的6在蓝色6的后面，当相同关键字的记录被划分到不同的子表时，可能会改变他们的顺序。因此希尔排序是一个不稳定的排序。

---