【无标题】

04-树5 Root of AVL Tree

分数 25

作者 陈越

单位 浙江大学

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

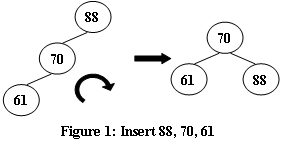
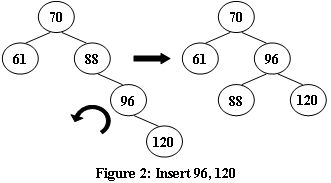
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

 

主要就是对AVL树的插入维护：

#include 
#include 
 
using namespace std;
 
typedef struct TNode* BinTree;
struct TNode
{
    int data;
    BinTree lchild,rchild;
    int height;
};
 
BinTree NewNode(int val);
int getHeight(BinTree root);
void updateHeight(BinTree& root);
int getBalanceFactor(BinTree root);
void L(BinTree& root);
void R(BinTree& root);
void Insert(BinTree &BST,int val);
int main()
{
    int n;
    scanf("%d",&n);
    BinTree BST=NULL;
    for(int i=0;i
    {
        int val;
        scanf("%d",&val);
        Insert(BST,val);
    }
    printf("%d\n",BST->data);
    return 0;
}
 
 
BinTree NewNode(int val)
{
    BinTree node=new TNode;
    node->data=val;
    node->height=1;
    node->lchild=node->rchild=NULL;
    return node;
}
 
int getHeight(BinTree root)
{
    if(root==NULL)
        return 0;
    else
        return root->height;
}
 
void updateHeight(BinTree& root)
{
    root->height=max(getHeight(root->lchild),getHeight(root->rchild))+1;
}
 
int getBalanceFactor(BinTree root)
{
    return getHeight(root->lchild) - getHeight(root->rchild);
}
 
void L(BinTree& root)
{
    BinTree temp=root->rchild;
    root->rchild=temp->lchild;
    temp->lchild=root;
    updateHeight(root);
    updateHeight(temp);
    root=temp;
}
 
void R(BinTree& root)
{
    BinTree temp=root->lchild;
    root->lchild=temp->rchild;
    temp->rchild=root;
    updateHeight(root);
    updateHeight(temp);
    root=temp;
}
 
void Insert(BinTree &BST,int val)
{
    if(!BST)
    {
        BST=NewNode(val);
        return;
    }
 
    if(valdata)
    {
        Insert(BST->lchild,val);
        updateHeight(BST);
        if(getBalanceFactor(BST)==2)
        {
            if(getBalanceFactor(BST->lchild)==1)
                R(BST);
            else if(getBalanceFactor(BST->lchild)==-1)
            {
                L(BST->lchild);
                R(BST);
            }
        }
    }
    else
    {
        Insert(BST->rchild,val);
        updateHeight(BST);
        if(getBalanceFactor(BST)==-2)
        {
            if(getBalanceFactor(BST->rchild)==-1)
                L(BST);
            else if(getBalanceFactor(BST->rchild))
            {
                R(BST->rchild);
                L(BST);
            }
        }
    }
}