第二章 OpenGL图形管线

1. OpenGL是整合软硬件的多平台2D和3D图形API

OpenGL

• 软件层提供c的接口调用
• 硬件层提供一个多级图形管线，并提供GLSL语言编程

2. OpenGL程序概览

3. OpenGL图形管线

• 顶点着色器：对顶点进行操作，主要处理顶点的位置
• 曲面细分着色器：用以生成大量三角形(TCS/TES)
• 几何着色器：以图元(三角形/点/四边形)为单位，可操作图元中的多个顶点，主要用于生成额外图元的能力
• 光栅化： 将3D世界的点、三角形展现到2D平面的显示器上，转化为以像素为单位的阵列(插值处理)
• 片段着色器：用于处理光栅化后的像素，指定像素颜色
• 像素操作：处理隐藏面消隐（HSR/z-buffer)

第三章 数学基础

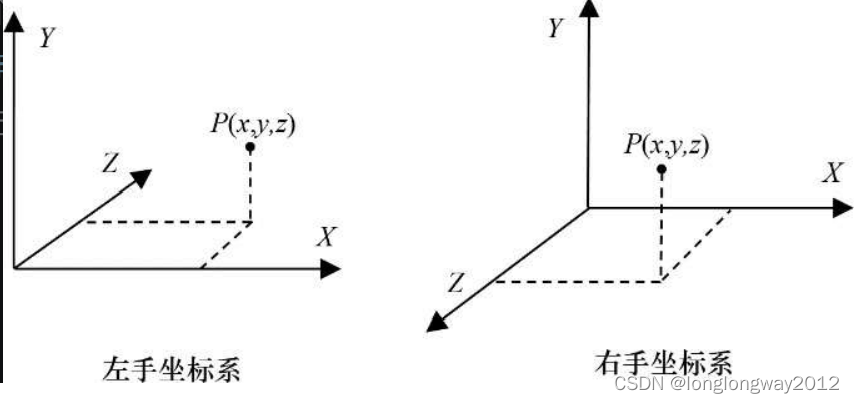
1. 3D坐标系

OpenGL使用右手系,DirectX使用左手系

2. 齐次坐标

• 点的表示(x,y,z,1)
• 向量(x,y,z,0)

3. 矩阵

• 矩阵分为行主序矩阵和列主序矩阵

• OpenGL使用列主序矩阵，计算乘法执行从左往右

• 矩阵类型

  • 单位矩阵
    [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ]

    [1000010000100001]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢1000010000100001⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
    ⎣ ⎡​1000​0100​0010​0001​⎦ ⎤​

  • 转置矩阵: 将矩阵的主对角线翻转，交换矩阵的行索引与列索引
    [ A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 ] = [ A 00 A 10 A 20 A 30 A 01 A 11 A 21 A 31 A 02 A 12 A 22 A 32 A 03 A 13 A 23 A 33 ] T

    [A00A01A02A03A10A11A12A13A20A21A22A23A30A31A32A33]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢A00A10A20A30A01A11A21A31A02A12A22A32A03A13A23A33⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}{A}_{00}& A_{01}& A_{02}& A_{03}\\ A_{10}& A_{11}& A_{12}& A_{13}\\ A_{20}& A_{21}& A_{22}& A_{23}\\ A_{30}& A_{31}& A_{32}& A_{33}\end{array}\right]$$
    =
    [A00A10A20A30A01A11A21A31A02A12A22A32A03A13A23A33]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢A00A01A02A03A10A11A12A13A20A21A22A23A30A31A32A33⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}{A}_{00}& A_{10}& A_{20}& A_{30}\\ A_{01}& A_{11}& A_{21}& A_{31}\\ A_{02}& A_{12}& A_{22}& A_{32}\\ A_{03}& A_{13}& A_{23}& A_{33}\end{array}\right]$$
    ^T ⎣ ⎡​A00​A10​A20​A30​​A01​A11​A21​A31​​A02​A12​A22​A32​​A03​A13​A23​A33​​⎦ ⎤​=⎣ ⎡​A00​A01​A02​A03​​A10​A11​A12​A13​​A20​A21​A22​A23​​A30​A31​A32​A33​​⎦ ⎤​T

  • 逆矩阵： $$A\ast A^{-1}=E$$ 或$$AB=BA=E$$

  • 正交矩阵：$$A{A}^T=E$$，即： 转置等于其逆的矩阵 $$A^T=A^{-1}$$

• 矩阵运算

  • 加法
    [ A + a B + b C + c D + d E + e F + f G + g H + h I + i J + j K + k L + l M + m N + n O + o P + p ] = [ A B C D E F G H I J K L M N O P ] + [ a b c d e f g h i j k l m n o p ]
    [A+aB+bC+cD+dE+eF+fG+gH+hI+iJ+jK+kL+lM+mN+nO+oP+p]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢A+aE+eI+iM+mB+bF+fJ+jN+nC+cG+gK+kO+oD+dH+hL+lP+p⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}A+a& B+b& C+c& D+d\\ E+e& F+f& G+g& H+h\\ I+i& J+j& K+k& L+l\\ M+m& N+n& O+o& P+p\end{array}\right]$$
    =
    [ABCDEFGHIJKLMNOP]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢AEIMBFJNCGKODHLP⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}A& B& C& D\\ E& F& G& H\\ I& J& K& L\\ M& N& O& P\end{array}\right]$$
    +
    [abcdefghijklmnop]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢aeimbfjncgkodhlp⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}a& b& c& d\\ e& f& g& h\\ i& j& k& l\\ m& n& o& p\end{array}\right]$$
    ⎣ ⎡​A+aE+eI+iM+m​B+bF+fJ+jN+n​C+cG+gK+kO+o​D+dH+hL+lP+p​⎦ ⎤​=⎣ ⎡​AEIM​BFJN​CGKO​DHLP​⎦ ⎤​+⎣ ⎡​aeim​bfjn​cgko​dhlp​⎦ ⎤​

• 乘法
  [ A X B Y C Z D E X F Y G Z H I X J Y K Z L M X N Y O Z P ] = [ A B C D E F G H I J K L M N O P ] × ( X Y Z )

  [AXBYCZDEXFYGZHIXJYKZLMXNYOZP]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢AXEXIXMXBYFYJYNYCZGZKZOZDHLP⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}AX& BY& CZ& D\\ EX& FY& GZ& H\\ IX& JY& KZ& L\\ MX& NY& OZ& P\end{array}\right]$$
  =
  [ABCDEFGHIJKLMNOP]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢AEIMBFJNCGKODHLP⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}A& B& C& D\\ E& F& G& H\\ I& J& K& L\\ M& N& O& P\end{array}\right]$$
  \times
  (XYZ)" role="presentation" style="position: relative;">⎛⎝⎜XYZ⎞⎠⎟$$\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)$$
  ⎣ ⎡​AXEXIXMX​BYFYJYNY​CZGZKZOZ​DHLP​⎦ ⎤​=⎣ ⎡​AEIM​BFJN​CGKO​DHLP​⎦ ⎤​×⎝ ⎛​XYZ​⎠ ⎞​

• 平移矩阵
  ( X + T x Y + T y Z + T z 1 ) = [ 1 0 0 T x 0 1 0 T y 0 0 1 T z ] × ( X Y Z )

  (X+TxY+TyZ+Tz1)" role="presentation" style="position: relative;">⎛⎝⎜⎜⎜X+TxY+TyZ+Tz1⎞⎠⎟⎟⎟$$\left(\begin{array}{c}X+T_x\\ Y+T_y\\ Z+T_z\\ 1\end{array}\right)$$
  =
  [100Tx010Ty001Tz]" role="presentation" style="position: relative;">⎡⎣⎢100010001TxTyTz⎤⎦⎥$$\left[\begin{array}{cccc}1& 0& 0& T_x\\ 0& 1& 0& T_y\\ 0& 0& 1& T_z\end{array}\right]$$
  \times
  (XYZ)" role="presentation" style="position: relative;">⎛⎝⎜XYZ⎞⎠⎟$$\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)$$
  ⎝ ⎛​X+Tx​Y+Ty​Z+Tz​1​⎠ ⎞​=⎣ ⎡​100​010​001​Tx​Ty​Tz​​⎦ ⎤​×⎝ ⎛​XYZ​⎠ ⎞​
  • 缩放矩阵
    [ X ∗ S x Y ∗ S y Z ∗ S z ] = [ S x 0 0 0 0 S y 0 0 0 0 S z 0 0 0 0 1 ] × [ X Y Z 1 ]
    [X∗SxY∗SyZ∗Sz]" role="presentation" style="position: relative;">⎡⎣⎢X∗SxY∗SyZ∗Sz⎤⎦⎥$$\left[\begin{array}{c}X\ast S_x\\ Y\ast S_y\\ Z\ast S_z\end{array}\right]$$
    =
    [Sx0000Sy0000Sz00001]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢⎢Sx0000Sy0000Sz00001⎤⎦⎥⎥⎥⎥$$\left[\begin{array}{cccc}{S}_x& 0& 0& 0\\ 0& S_y& 0& 0\\ 0& 0& S_z& 0\\ 0& 0& 0& 1\end{array}\right]$$
    \times
    [XYZ1]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢XYZ1⎤⎦⎥⎥⎥$$\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$
    ⎣ ⎡​X∗Sx​Y∗Sy​Z∗Sz​​⎦ ⎤​=⎣ ⎡​Sx​000​0Sy​00​00Sz​0​0001​⎦ ⎤​×⎣ ⎡​XYZ1​⎦ ⎤​
  • 右手系转左手系矩阵
    [ 1 0 0 0 0 1 0 0 0 0 − 1 0 0 0 0 1 ]
    [1000010000−100001]" role="presentation" style="position: relative;">⎡⎣⎢⎢⎢1000010000−100001⎤⎦⎥⎥⎥$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& 1\end{array}\right]$$
    ⎣ ⎡​1000​0100​00−10​0001​⎦ ⎤​
    

  旋转矩阵的数值很是类似，个人总结了以下规律：

  • 条件：
    • 右手坐标系，列主序矩阵
    • 旋转方向：从开始轴到目标轴
  • 被旋转的轴所对应的矩阵分量值不变
  • 起始轴向目标轴旋转，目标轴$sin(\theta )$值前加负号
  • 左侧列总为：$cos(\theta ),sin(\theta )$组合
  • 右侧列总为: $sin(\theta ),cos(\theta )$组合

• 投影矩阵

  • 透视投影
    

  • 正交投影
    
    投影矩阵范围中，z方向的范围为[0,1]（opengl投影矩阵z方向为[-1,1]，可以参考opengl编程指南附录部分)

  • LookAt矩阵
    
    

  4. 向量运算

  • 加减
    $$A\pm B=(u\pm x,v\pm y,w\pm z)$$

  • 点积
    $$A\cdot B=(ux+vy+wz)$$

  • 叉积
    $$A\times B=(vz-wy,wx-uz,uy-vx)$$

关注公众号