• （五）算法基础——分治

    目录

    基本概念

    实例

    称硬币 

    例子

    归并排序

    快速排序

    例题

    输出前m大的数

    求排列的逆序数

    基本概念

            把一个任务，分成形式和原任务相同，但规模更小的几个部分任务（通常是两个部分），分别完成，或只需要选一部完成。然后再处理完成后的这一个或几个部分的结果，实现整个任务的完成。

    实例

    称硬币 

            16硬币，有可能有1枚假币，假币比真币轻。有一架天 平，用最少称量次数确定有没有假币，若有的话，假 币是哪一枚。

            这个我们之前应该接触过，解决办法就是一次一次不断分解，两边先称8个，然后4个，然后两个，最后一个，就能得出结果。 

    1. 8 – 8 一称，发现无假币，或假币所在的那8枚
    2. 4 – 4 一称
    3. 2 – 2 一称
    4. 1 – 1 一称

    例子

    归并排序

    步骤

    数组排序任务可以如下完成：

    1. 把前一半排序
    2. 把后一半排序
    3. 把两半归并到一个新的有序数组，然后再拷贝回原 数组，排序完成。

    代码实现

    1. #include
    2. void Merge(int a[],int s,int m, int e,int tmp[]) 
    3. {
    4. //将数组a的局部a[s,m]和a[m+1,e]合并到tmp,并保证tmp有序，然后再拷贝回a[s,m]
    5. //归并操作时间复杂度：O（e-m+1),即O（n)
    6. int pb = 0,i;
    7. int p1 = s,p2 = m+1; // 两个指针，比较大小，把小的放入数组之后再移动 
    8. while( p1 <= m && p2 <= e) {
    9. 	if( a[p1] < a[p2]) 
    10. 		tmp[pb++] = a[p1++];
    11. 	else 
    12. 		tmp[pb++] = a[p2++];
    13. 	}
    14. 	while( p1 <= m) // 一个数组以及完成，将另一个数组放入 
    15. 		tmp[pb++] = a[p1++];
    16. 	while( p2 <= e)
    17. 		tmp[pb++] = a[p2++];
    18. 	for(i = 0;i < e-s+1; ++i)// 拷贝 
    19. 	a[s+i] = tmp[i];
    20. }
    21. // 归并排序 
    22. void MergeSort(int a[],int s,int e,int tmp[])
    23. {
    24. 	if( s < e) {
    25. 		int m = s + (e-s)/2;
    26. 		MergeSort(a,s,m,tmp);
    27. 		MergeSort(a,m+1,e,tmp);
    28. 		Merge(a,s,m,e,tmp);
    29. 	}
    30. }
    31.  
    32. int a[10] = { 13,27,19,2,8,12,2,8,30,89};
    33. int b[10]; 
    34. int main()
    35. {
    36. int size = sizeof(a)/sizeof(int),i;
    37. MergeSort(a,0,size-1,b);
    38. for(i = 0;i < size; ++i)
    39. 	printf("%d ",a[i]);
    40. return 0;
    41. }

            可能有些同学对归并函数（Merge）不是特别熟悉，我们来简单的介绍一下。就是通过两个指针，不断比较大小，然后得到有序数组。

     

    时间复杂度 

            归并排序的时间复杂度是O(nlog(n))，具体证明方法如下，就不做详细介绍。

    对n个元素进行排序的时间：

    • T(n) = 2*T(n/2) + a*n (a是常数,具体多少不重要）
    • = 2*(2*T(n/4)+a*n/2)+a*n
    • = 4*T(n/4)+2a*n
    • = 4*(2*T(n/8)+a*n/4)+2*a*n
    • = 8*T(n/8)+3*a*n ...
    • = 2k *T(n/2k)+k*a*n 一直做到 n/2k = 1 (此时 k = log2n)，
    • T(n)= 2k *T(1)+k*a*n = 2k *T(1)+k*a*n = 2k+k*a*n = n+a*(log2n)*n

            复杂度O(nlogn)

    快速排序

    步骤

    数组排序任务可以如下完成：

    1. 设k=a[0], 将k挪到适当位置，使得比k小的元素都 在k左边,比k大的元素都在k右边，和k相等的，不关心 在k左右出现均可 （O（n)时间完成）
    2. 把k左边的部分快速排序
    3. 把k右边的部分快速排序

            1、将第一个元素设为K,偶数时用 j 去比较 i ，如果 j 小于 i ，则交换 i 与 j 的位置。如果 j 大于 i，j --。

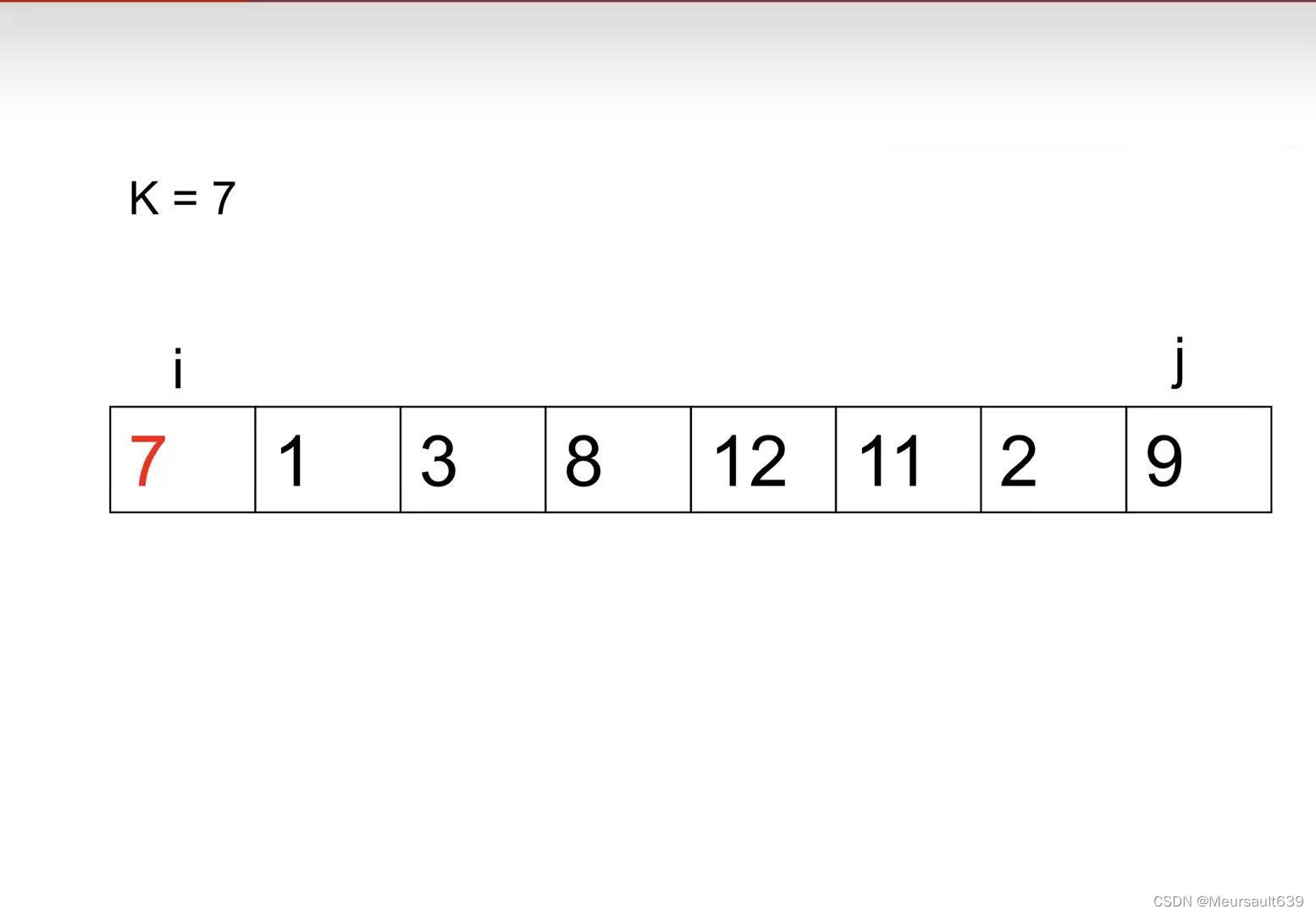
    j --; 

    中南大学算法实验报告
    docx 0星 超过10%的资源 106KB
    下载

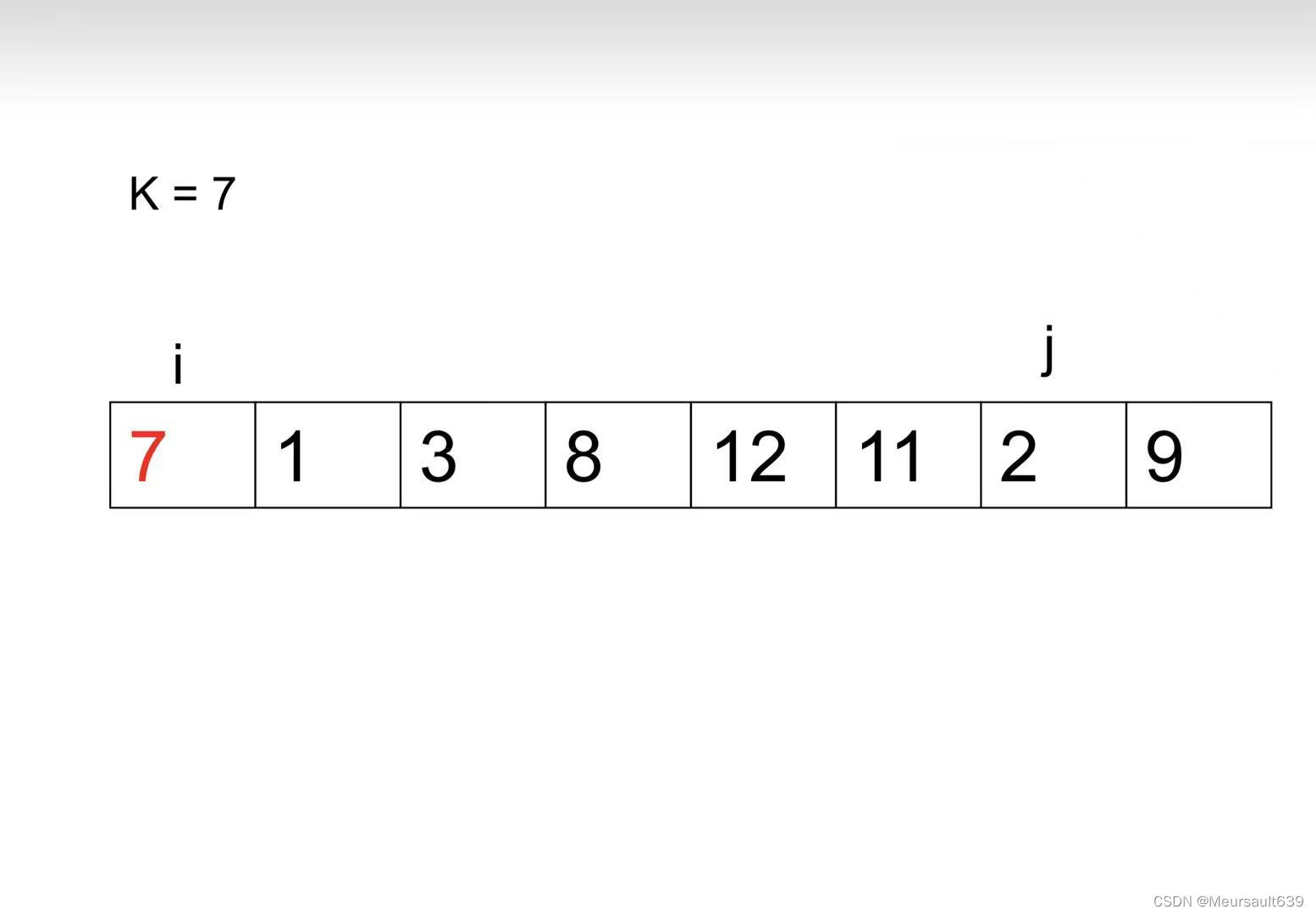
     交换；

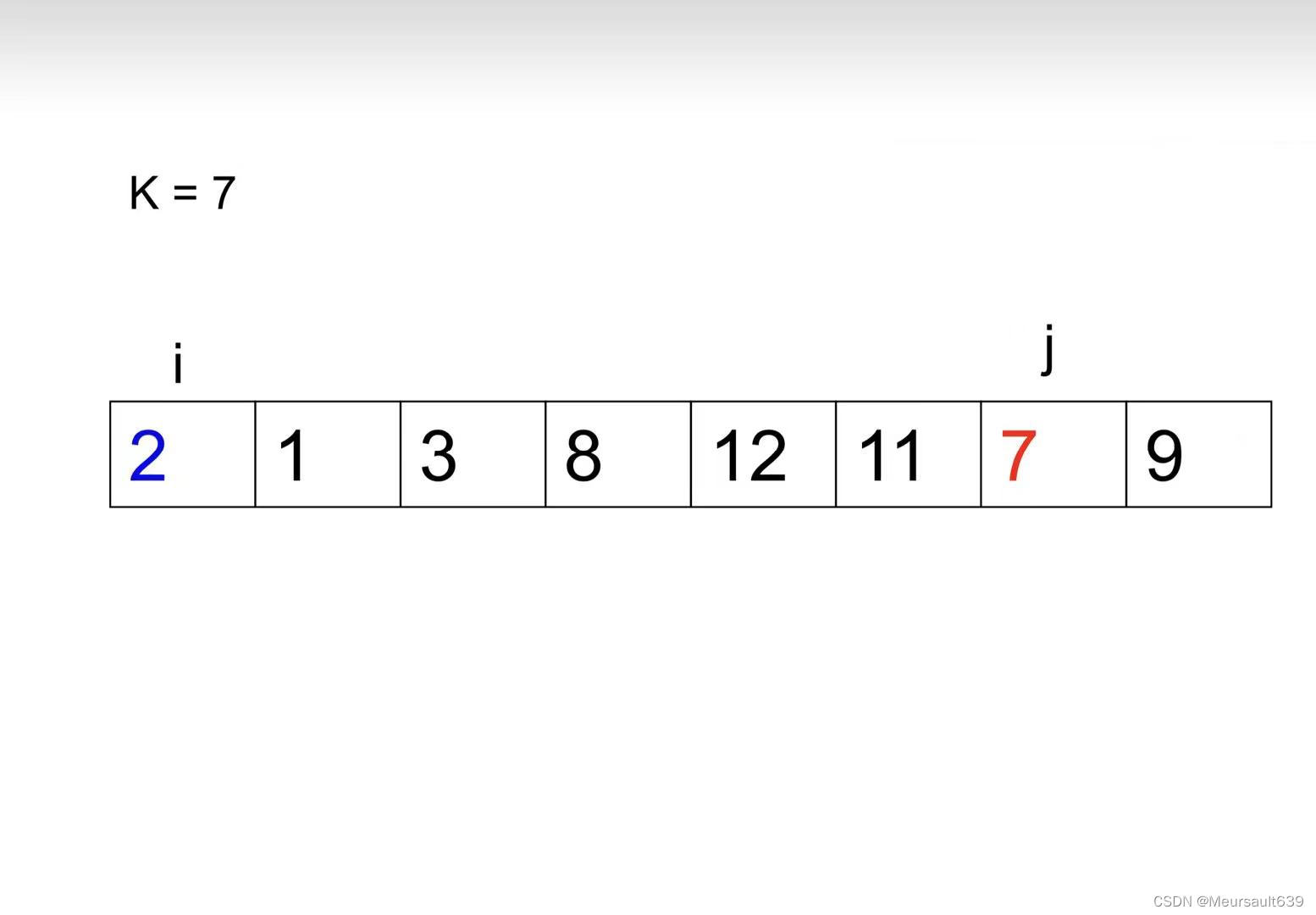
            2、 当交换次数为奇数时，用 i 去比较 j ，如果 i 小于 j ，i++。如果 i 大于 j，则交换 i 与 j 的位置。

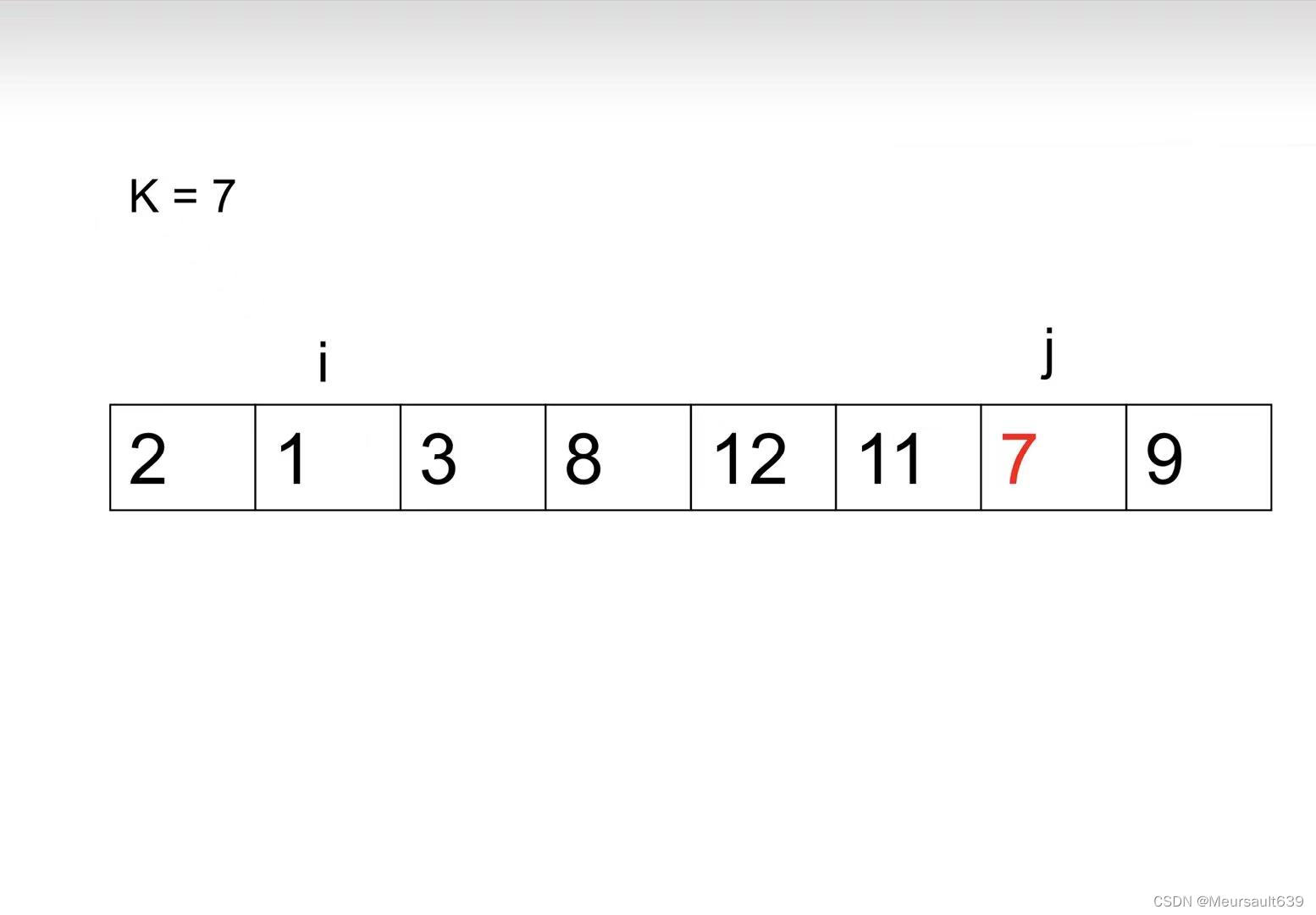
    i++; 

     

    交换； 

     

     

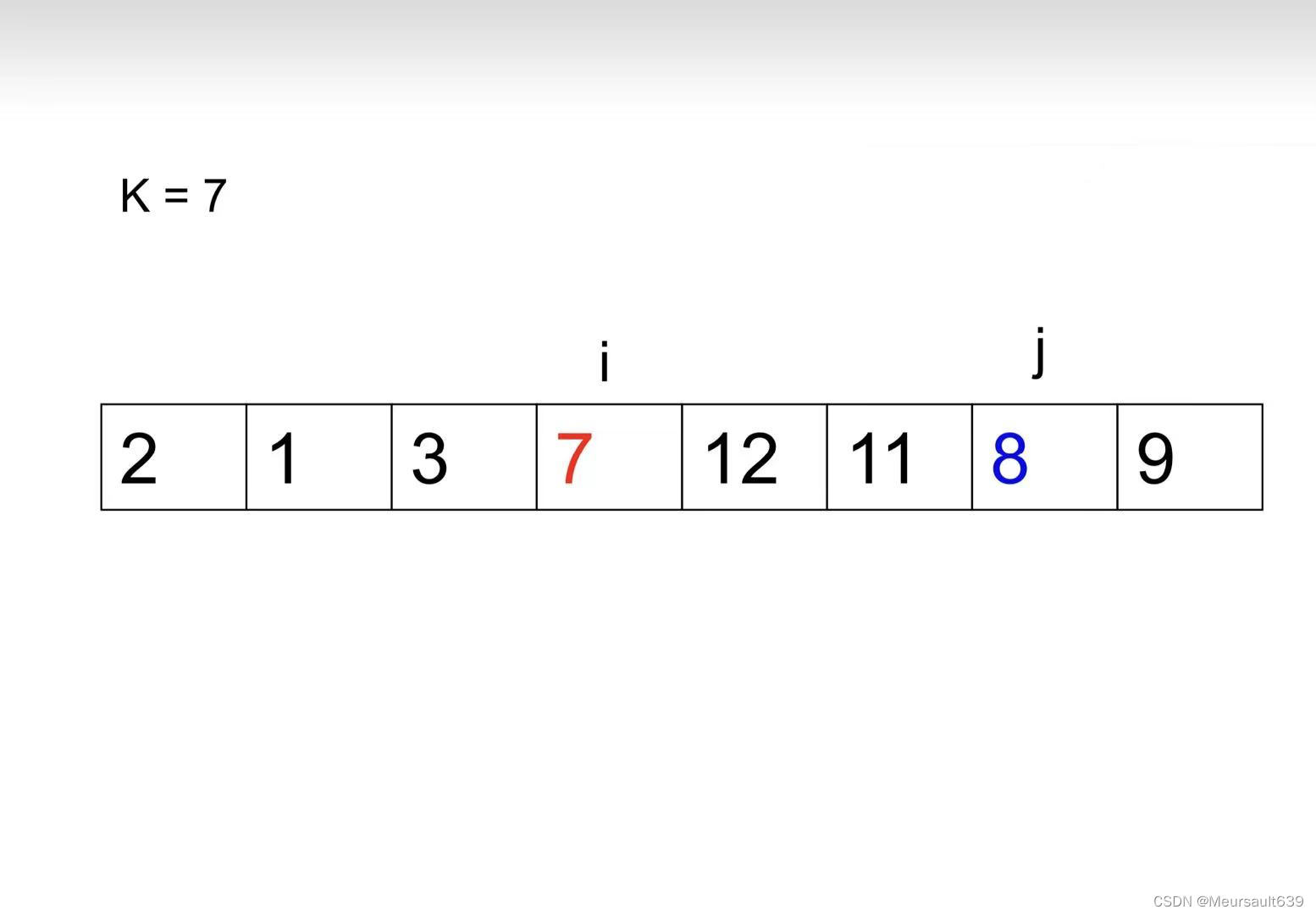
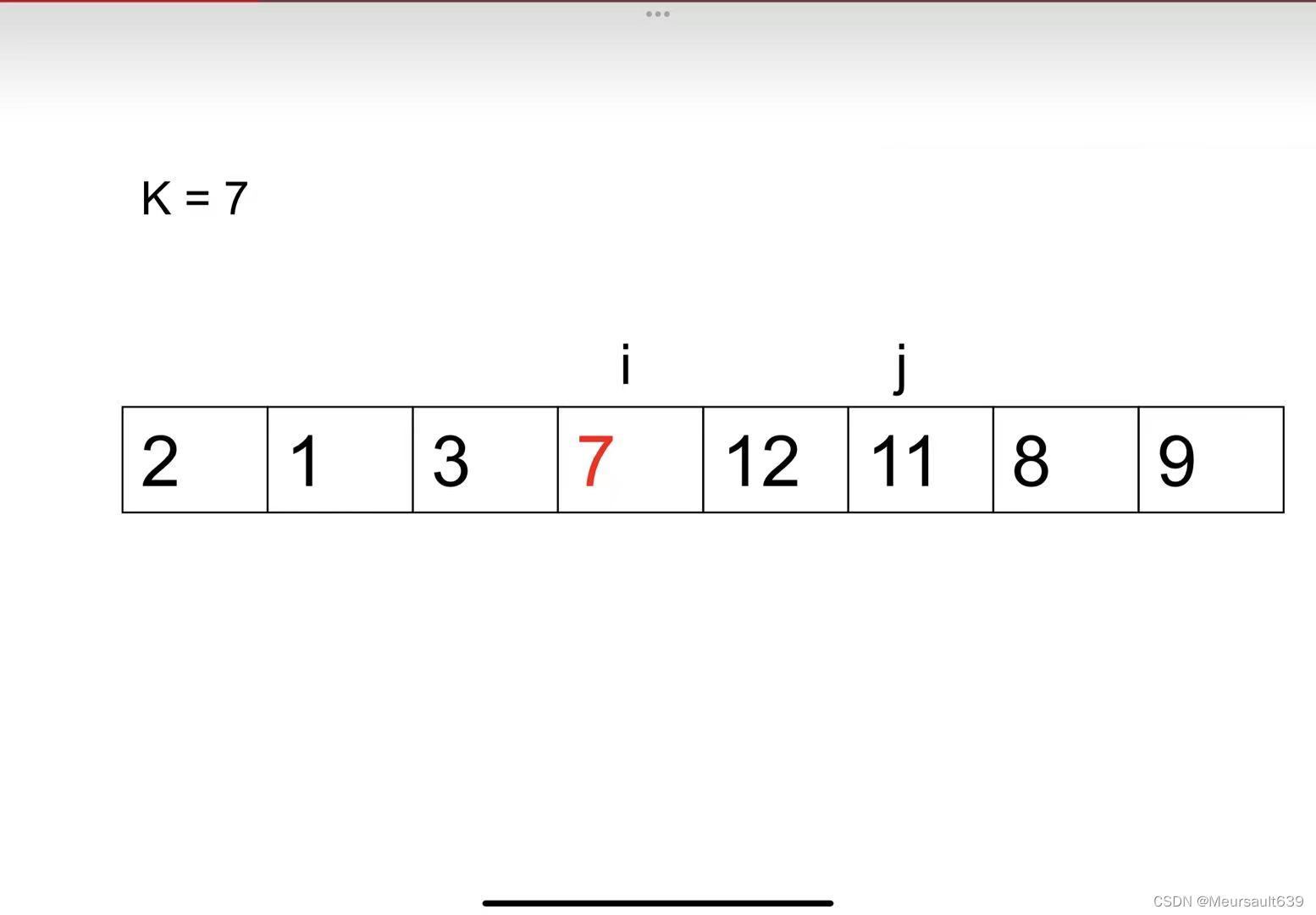
            3、j=i,停止。 

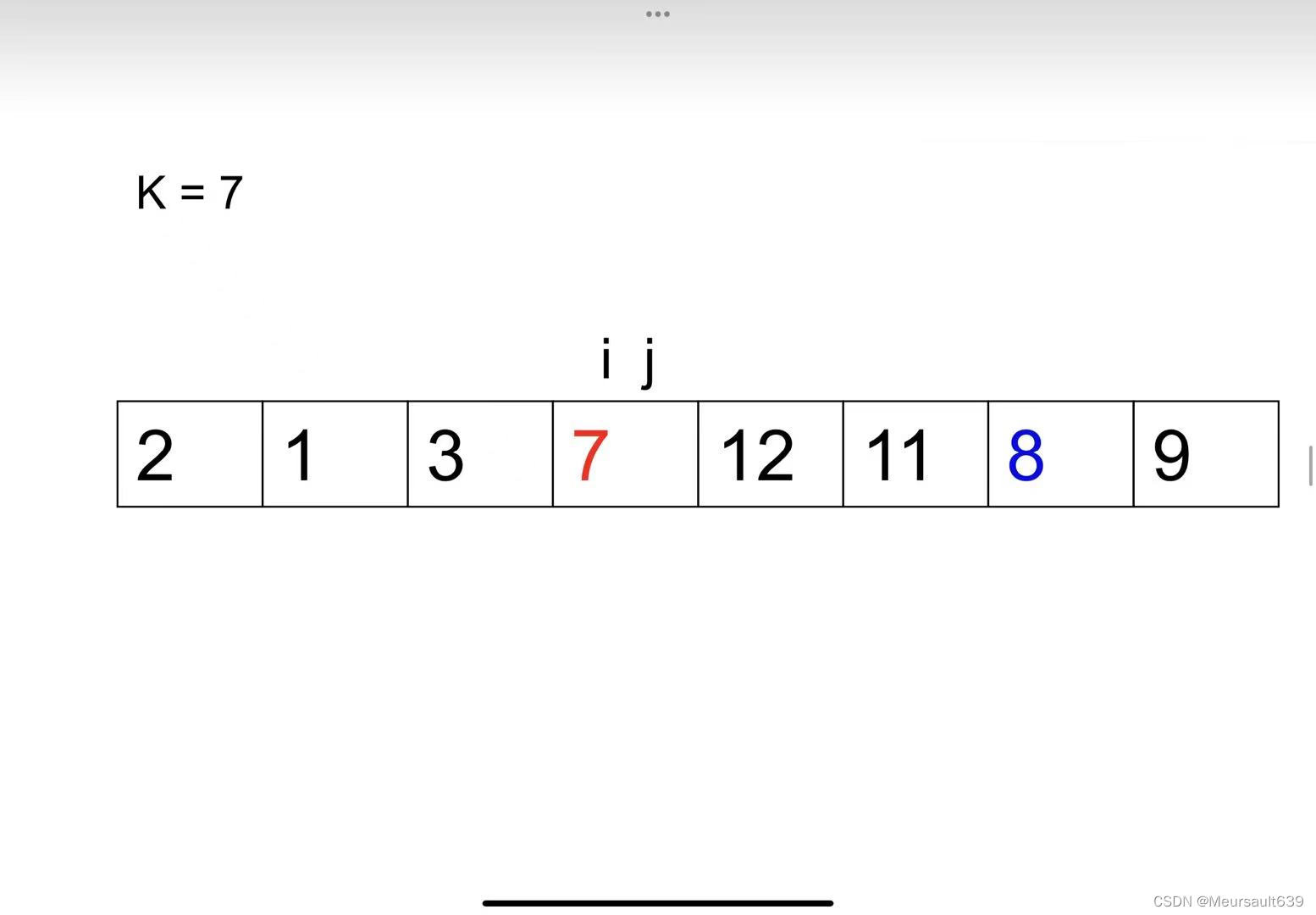
    代码如下

    1. #include
    2. void swap(int * a,int * b) //交换变量a,b值
    3. {
    4. 	int tmp = *a;
    5. 	*a = *b;
    6. 	*b = tmp;
    7. }
    8. void QuickSort(int a[],int s,int e)
    9. {
    10. 	if( s >= e)
    11. 		return;
    12. 	int k = a[s];
    13. 	int i = s,j = e;
    14. 		while( i != j ) {
    15. 			while( j > i && a[j] >= k )
    16. 				--j;
    17. 			swap(&a[i],&a[j]);
    18. 			while( i < j && a[i] <= k ) 
    19. 				++i;
    20. 			swap(&a[i],&a[j]);
    21. 	} //处理完后，a[i] = k
    22. 	QuickSort(a,s,i-1);
    23. 	QuickSort(a,i+1,e);
    24. }
    25. int a[] = { 93,27,30,2,8,12,2,8,30,89};
    26. int main()
    27. {
    28. int size = sizeof(a)/sizeof(int),i;
    29. QuickSort(a,0,size-1);
    30. for(i = 0;i < size; ++i)
    31. 	printf("%d ",a[i]);
    32. return 0;
    33. }

            时间复杂度也是 O(nlogn)，就不做过多介绍。

    例题

    算法设计与分析课程ppt全集
    zip 0星 超过10%的资源 4.60MB
    下载

    输出前m大的数

    • 描述

            给定一个数组包含n个元素，统计前m大的数并且把这m个数从大到小输出。

    • 输入

            第一行包含一个整数n，表示数组的大小。n < 100000。 第二行包含n个整数，表示数组的元素，整数之间以一个空格分开 。每个整数的绝对值不超过100000000。 第三行包含一个整数m。m < n。

    • 输出

            从大到小输出前m大的数，每个数一行。

    解题思路

            首先是可以选择先排序再输出，复杂度是  O(nlogn)；但是除此之外，还可以选择用分治的思想把前m大的都弄到数组最右边，然后对这最右边m个元素排序， 再输出。这样的话复杂度是O(n+mlogm)，在大部分情况下，比第一种解法要更好。

    操作

    如何将前k大的都弄到最右边

    1. 设key=a[0], 将key挪到适当位置，使得比key小的元素都在 key左边，比key大的元素都在key右边（线性时间完成）
    2. 选择数组的前部或后部再进行 arrangeRight操作

    具体如下所示

     

    1. #include
    2. void swap(int * a,int * b) //交换变量a,b值
    3. {
    4. 	int tmp = *a;
    5. 	*a = *b;
    6. 	*b = tmp;
    7. }
    8. void arrangeRight(int a[],int s,int e,int m)
    9. {
    10. 	if( s >= e)
    11. 		return;
    12. 	int k = a[s];
    13. 	int i = s,j = e;
    14. 		while( i != j ) {
    15. 			while( j > i && a[j] >= k )
    16. 				--j;
    17. 			swap(&a[i],&a[j]);
    18. 			while( i < j && a[i] <= k ) 
    19. 				++i;
    20. 			swap(&a[i],&a[j]);
    21. 	} //处理完后，a[i] = k
    22. 	
    23. 	if(e-i == m){
    24. 		return;
    25. 		//a = k return 
    26. 	}
    27. 	if(e-i > m){
    28. 		return arrangeRight(a,i+1,e,m);
    29. 		//a > k 对最右边a-1个元素再进行arrangeRigth
    30. 	}
    31. 	if(e-i < m){
    32. 		return arrangeRight(a,0,i-1,m-e+i);
    33. 		//a < k 对左边b个元素再进行arrangeRight
    34.  
    35. 	}
    36. }
    37. // 快排其实可以用自带的函数，但我还是用了上面自己写的。 
    38. void QuickSort(int a[],int s,int e)
    39. {
    40. 	if( s >= e)
    41. 		return;
    42. 	int k = a[s];
    43. 	int i = s,j = e;
    44. 		while( i != j ) {
    45. 			while( j > i && a[j] >= k )
    46. 				--j;
    47. 			swap(&a[i],&a[j]);
    48. 			while( i < j && a[i] <= k ) 
    49. 				++i;
    50. 			swap(&a[i],&a[j]);
    51. 	} //处理完后，a[i] = k
    52. 	QuickSort(a,s,i-1);
    53. 	QuickSort(a,i+1,e);
    54. }
    55. int main(void)
    56. {
    57. 	int i,m,n,x;
    58. 	scanf("%d",&n);
    59. 	int a[n];
    60. 	for(i = 0;i < n; ++i)
    61. 		scanf("%d",&a[i]);	
    62. 	scanf("%d",&m);
    63. 	//分治 
    64. 	arrangeRight(a,0,n-1,m);
    65. 	//排序 
    66. 	QuickSort(a,m,n-1);
    67. 	//输出 
    68. 	for(i = n-m;i < n; ++i)
    69. 		printf("%d ",a[i]);
    70. 	return 0;
    71. }

    求排列的逆序数

    题目

            考虑1,2,…,n (n ik， 那么就称(ij ,ik )是这个排列的一个逆序。 一个排列含有逆序的个数称为这个排列的逆序数。例如排列 263451 含有8个 逆序(2,1),(6,3),(6,4),(6,5),(6,1),(3,1),(4,1),(5,1)，因此该排列的逆序数就是8。 现给定1,2,…,n的一个排列，求它的逆序数。

    解题思路

            一开始当然是可以用遍历去解决，但是那样时间复杂度为 O(n^2 )，所以我们采用分治的方法去解决。其实也就是归并排序，其实仔细想想，就会发现需要我们求得刚好就是我们按照升序排序时移动元素的次数。所以我们只需要在之前的归并排序上改动一点点，就能实现我们的需求。

    代码实现如下

             我没有加上输入，这个比较简单，大家稍作修改就好了。

    1. #include
    2. int sum = 0;
    3. void Merge(int a[],int s,int m, int e,int tmp[]) 
    4. {
    5. //将数组a的局部a[s,m]和a[m+1,e]合并到tmp,并保证tmp有序，然后再拷贝回a[s,m]
    6. //归并操作时间复杂度：O（e-m+1),即O（n)
    7. int pb = 0,i;
    8. int p1 = s,p2 = m+1; // 两个指针，比较大小，把小的放入数组之后再移动 
    9. while( p1 <= m && p2 <= e) {
    10. 	if( a[p1] < a[p2]) 
    11. 		tmp[pb++] = a[p1++];
    12. 	else {
    13. 		tmp[pb++] = a[p2++];
    14. 		sum += m-p1+1; // 计数
    15. 	}
    16. 		
    17. 	}
    18. 	while( p1 <= m) // 一个数组以及完成，将另一个数组放入 
    19. 		tmp[pb++] = a[p1++];
    20. 	while( p2 <= e)
    21. 		tmp[pb++] = a[p2++];
    22. 	for(i = 0;i < e-s+1; ++i)// 拷贝 
    23. 	a[s+i] = tmp[i];
    24. }
    25. // 归并排序 
    26. void MergeSort(int a[],int s,int e,int tmp[])
    27. {
    28. 	if( s < e) {
    29. 		int m = s + (e-s)/2;
    30. 		MergeSort(a,s,m,tmp);
    31. 		MergeSort(a,m+1,e,tmp);
    32. 		Merge(a,s,m,e,tmp);
    33. 	}
    34. }
    35.  
    36. int a[6] = { 2,6,3,4,5,1};
    37. int b[6]; 
    38.  
    39. int main()
    40. {
    41. int size = sizeof(a)/sizeof(int),i;
    42. MergeSort(a,0,size-1,b);
    43. 	printf("%d",sum); // 输出
    44. return 0;
    45. }
  • 相关阅读:
    win11开机音效设置的方法
    2022腾讯全球数字生态大会【存储专场】它来了|预约有礼
    大厂光环下的功能测试，出去面试自动化一问三不知
    【python学习】基础篇-常用模块-multiprocessing模块：多进程
    18.3 NPCAP 构建中间人攻击
    【算法刷题】链表篇-删除链表中的重复节点
    #Day Day Plan# 《NCB_PCI_Express_Base 5.0.1.0》pdf 译文笔记
    FFmpeg入门详解之69：ffmpeg.c（4.3.1）源码剖析
    c语言编程题经典100例
    手把手教你编写LoadRunner脚本
  • 原文地址：https://blog.csdn.net/weixin_66578482/article/details/126068830