MySQL (6)

前言：

本文 内容 将完成 上文 聚合查询中 未完成的几个 查询 如 ： 子查询， 合并查询， 然后会讲到 面试常考 的 索引。
 
 

在此 之前我们 来 回顾 一下上文 讲到过的 内容 ：
 
 

1.表的 设计
 
 

总结:

先找 实体，再找关系，实体就算 关键性的 名词，每个实体都需要分配成 一张表，然后我们还需要考虑 实体与 实体之间的 关系 不同的关系 在设计表 又会 有 不同 的设计 方式 ，如 一对一 ，一 对 多， 多对多。
 

1. 一对一 ：
    
   ​ 每个中国本土居民和他们唯一的身份证编号。

 

2. 一对多
    
   一个年级段有多个平行班级，多个平行班都隶属于一个年级段。

    

3. 多对多
    
   一个班级有若干个老师，一个老师也可以带若干个班级。

 

新增： 和查询 操作 结合 在一起 的 新增 操作 语法 : insert into B select * from A (将 查询 到 A 的 记录 全部插入 到B 中)
 
注意: 这里 可以 通过 指定 列 来 对准 需要插入 的数据类型。
 

聚合查询： 行和行 之间 的数据加工

 

聚合 函数
 

函数	说明
count( 列名 / 表达式 )	返回查询到的数据的 数量（查询结果有多少行）
sum (列名 / 表达式)	返回查询到的数据的 总和，不是数字没有意义
avg (列名 / 表达式)	返回查询到的数据的 平均值，不是数字没有意义
max (列名 / 表达式)	返回查询到的数据的 最大值，不是数字没有意义
min (列名 / 表达式)	返回查询到的数据的 最小值，不是数字没有意义

 

分组操作 ： group by 根据行的值，对数据进行分组，把值相同的行都归为一组。
 
此时 每个组 又可以分别 的进行 聚合查询了，分组还可以指定条件筛选，如果是分组之前指定的条件，使用where如是分组之后使用 having
 

联合查询（多表查询） 和前面的 单表查询 相对应。
 

关键操作 笛卡尔积。
 

回忆 完成 下面 让我们 进入 本文的 学习， 这里我们 先来 学习 一下 自连接
 

联合查询(多表查询)

 

自连接

 

自连接， 是 把 自己和 自己 进行笛卡尔积
 
这里 属于 SQL 中 的 一种 奇淫巧计 （使用的 不多，只是 用来处理 一些特殊的场景的问题）。
 

那么 这里 就有 一个 问题 啥时候 需要使用 自连接呢？
 
这里我们 来 了解 一下 自连接 的 本质 ，自连接 其实 是把行和行 之间的比较条件 转化为 列和 列。

 

回忆 一下我们之间 的 SQL 操作 是不是 通过 SQL 指定 条件 ，按照 列和列之间进行指定的。
 

这里 拿出 以前 创建 的 exam_result 这张表 ，

 

这里 我们的 列和 列 查找 是不是 非常 好找 ，但是 有的时候我们 并不能直接 进行列和列的 查找，可以 会是 行和行
 

这里就来 举个例子
 

演示：显示所有“计算机原理”成绩比“Java”成绩高的成绩信息 这里我们 的问题 是 科目 之间 的分数比较 这 并不是 针对列 和 列 了 而是 针对 行和 行 了。
 
1.这里我们 还是 拿 这 4 张 表 来 看

 

2. 进行 笛卡尔积操作 ，添加 条件 完成 题目。
    

 
3.最后得出来 的 表格 是不是 有点 不好看 我们 可以 通过别名 进行 更改
 

总结 ： 自连接的关键所在 就算能把行转化成列（对自己使用笛卡尔积操作）。
 

子查询

 

这里 子查询 我们 只需了解 即可（因为面试 可以 会考）， 以后 工作 几乎 用不到。

子查询是指嵌入在其他sql语句中的select语句，也叫嵌套查询
 

也就是 将 多个 select 合并成 一个 ， 简单 来说 就是 套娃， 他能 一直套娃下去。
 
 

这里 扩充一下 ：
 
人脑的内存空间是是非常小的，硬盘很大，CPU 对于 返点数计算非常弱，但是对于图像意识非常强。'=
 
人脑同时一时刻一共能维护几个变量。 据研究受过专业的训练的人大概是7个
 
回忆一下
 
Java编程中，经常谈到的“封装”，都是顺着人脑的特点来展开的。
 

封装的目的就是让人脑一次只关注一个点，不用考虑过多细节。
 

如果需要考虑细节，进入细节里面考虑，又不必考虑上层的逻辑。
 

java里面的一些代码太过复制的时候，就需要将其拆分成多个方法，多个类来实现。
 

子查询就是做着与Java 编程相反的事情：将拆分好的代码给合并成一个。
 

使得代码的阅读性大大降低。所以这不是一个推荐用的操作。
 

单行子查询：返回一行记录的子查询

 

演示 ： 查找 不想毕业同学 的 同班 同学

 

这里我们 就需要 先 知道 不想毕业 这个同学 的班级 id 然后 根据 班级 id 在 学生表中 筛选 相同 班级 id 的 同学

 

1.查找不想毕业 同学的班级id
 

 

2.通过 不想毕业同学的 班级 id 在学生表 找 相同班级id 的同学
 

 

上面 就是我们 正常 的 操作 流程 分为 两步 ，而 子查询 就 需要 一步 下面我们来 看一看。
 

别看 现在 这个 子查询 简单，如果我们 套了 10个 8 个 SQL 呢 你还会觉的 子查询 简单吗？
 

多行子查询：返回多行记录的子查询

 
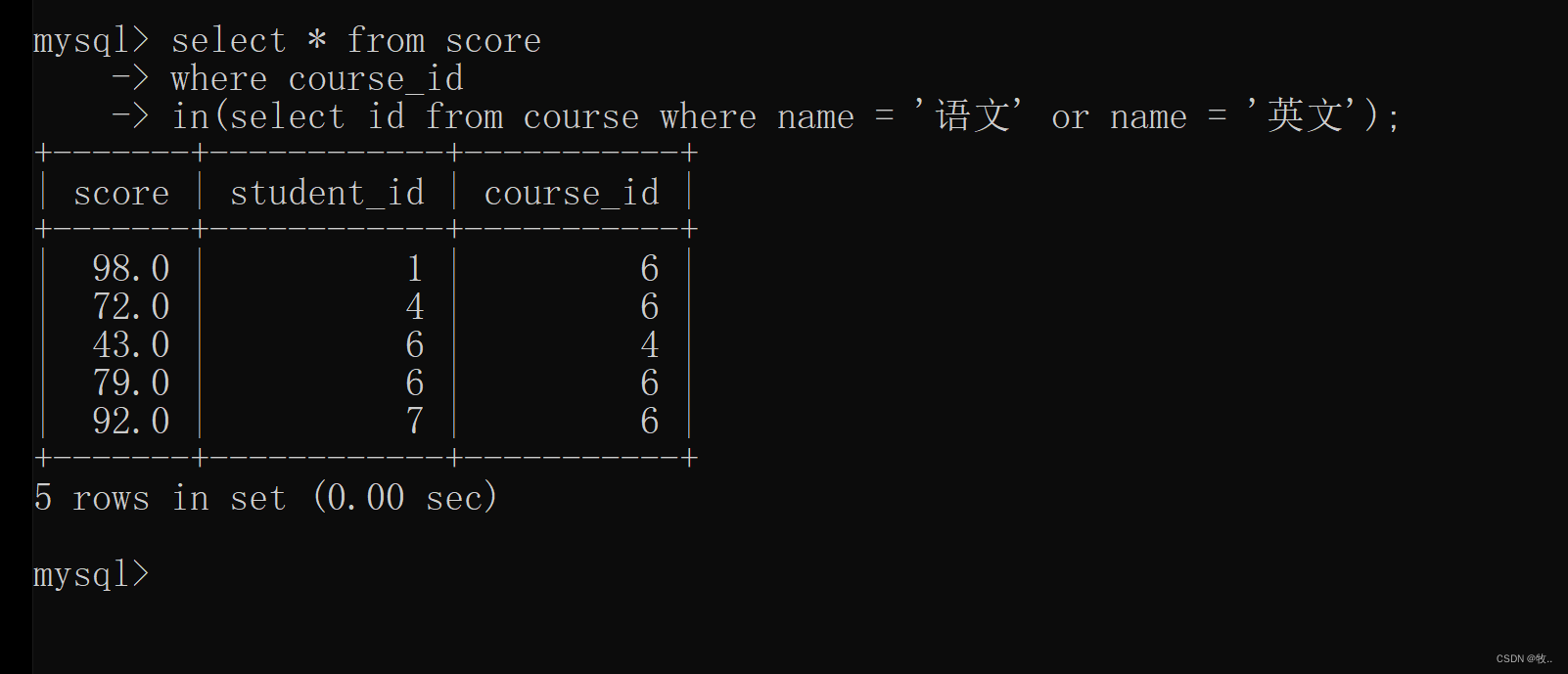
有的时候 子查询 可能 会 查询 出多条记录 ， 这里 就不能直接 使用 等号 = , 可能 需要 用到 in 这样的 一些 操作。

 

演示 ：查询 语文 或 英文课程 的 成绩信息

 

这里 我们 就需要 先查询 语文 和 英语 的课程 id 再根据课程id 找到 对应 的 成绩 信息。
 
1.查找 语文 或 英文的课程 id

2.查找 语文 或 英文 的成绩
 

 

这我们 就通过 多行子查询，将这两个 操作和 在一起。
 

补充：

在 子查询 中 除了 能使用 关键字 in , 其实 能 使用 关键字 [not] exists
 

[not] exists 关键字： 这里 我们 的 exists 属于 既 执行 效率 低 有难以 理解 ，如果 感兴趣 可以 自行 百度 了解，这里 就 不展开。

 

 

合并查询

 
合并查询 ： 将 多个 查询 语句 的结果 结合 并到 一起。

 

这里 我们 可以 使用 union 和 union all （如果 你 学过 c 语言 ，那么 肯定 了解 过 这个 union 他就代表 我们的 联合体 用一块内存表示不同内存的含义）
 
通过 union 把 两个 sql 的查询 结果 结合 合并 到 一起。
 
合并的前提是 两个sql 查询 的列得是对应的 （如 表中 的 没一列 类型 对应 ）。
 

这里 就来 演示一下。
 
查询 id 小于 3 或者 名字 为 英文 的 课程
 

 

这里我们 还可以 使用 or 来 完成
 

但是 这里 使用 or 必须 保证 针对 同一张表 指定 的 多个 条件 ，但 合并查询 union 不一定 正对 同一张表。
 

最后 ：union 和 union all 的 区别 是 union 会 自动 去重， 而 union all 不会 去重。
 

 
下面我们进入 MySQL 中 的 索引
 

 
这里我们 稍微 回忆 一下 之前的 内容，可以发现 ，他们都是 属于 操作 层面的 ， 没有太大难度，封顶 多表查询 稍微 有点难度， 只要 多 练习一下 就能掌握，

 

下面我们 要学习 MySQL 中 的 索引和 事物 ，都是 属于 MySQL 原理 层面的 东西 。

 

涉及到一些MySQL内部的一些实现机制， 该内容比较抽象。而且 MySQL 是一个背后非常庞大的软件 ， 内部的原理和机制，数不胜数，
 
（如果 你的 岗位 是 普通 程序员，这些东西 ，很少用的 到 ，为啥 这里 要学 呢， 单纯 就是 应付 面试 中 的 提问）。

 

索引

 
索引 （index） 相当于 一本书 的 目录 （index） 可以看到 他们的 英文 相同 这里 指的 是 同一个东西 只不过表型形式不一样
 

索引 的 概念 与 作用

 

索引 的优缺点

 
这里 继续 拿书 进行 举例：
 
我们 书 的 目录 一旦 确定 了 ，后续 每次 对 书 的内容 都可能 会影响 到 目录的 准确性，就需要重新 调整 目录  

这里 数据库 的 索引 也是 一样的 ，当 进行 增删改的时候 ，往往 也需要同步的调整索引的结构。

 

这里我们 来 看看 索引的 优缺点：
 

索引 带来 的好处 ：提高了 查找的 速度。
 

索引 带来的 坏处 ： 1. 占用 了 更多 的 空间， 2. 拖慢了增 删 改 的 速度。

 

有没有 同学 认为 坏处 有 两条 好处 有 一条， 这里 索引 就 不太好， 其实

 

从表面来上看，似乎索引的坏处 比 索引带来的好处要多。但！这不必意味着 弊大于利！！ 因为在实际需求的场景中，查询操作往往是最高频率的操作。
 

相对于“增删改” 的使用频率则低的可怜。 因此，查询作为一个高频操作，索引对其来说是不可缺少的，
  

另外，有了索引之后对于查询的效率的提升使非常巨大的！！！
 

当MySQL里面的数据量级 达到千万级别的时候（一个表里就有几千万，甚至破亿的数据）再去遍历表，就会非常非常的低效！！！
 

且 MySQL 在进行 比较 的 时候 不是

for(int i = 0; i< 1Kw ;i++){
	if(arr[i] == num){
		break;
	}
}
1
2
3
4
5

通过 一个 for 循环 来完成 的 ， 这个 查找是 在 内存 中 的 比较， 而MySQL 中 的比较 是在硬盘上 的， 每次 比较 会 涉及 到 硬盘上的 IO 操作，

 

且 硬盘 IO 的 速度 比内存 的 速度 慢 3 - 4 个 数量级 （数几万倍） 。 这里 使用 for 循环 查询 就会 非常非常慢
 

这了 就 有 了索引 操作，就能提高 数几万倍 的查询速度。

 

概念 作用 和 优缺点 了解完 我们来 了解了解 ， 索引 的 一些 SQL 操作。

 

索引 的 一些SQL 操作

 

1.查看 索引

 
语法 ：show index from 表名 查看 一个表上 都有那些 索引 。
 

 

2.创建索引

 
给 一个 表 中 某 一列 来创建 索引
 

语法 ： create index 索引名字 on 表名 （列名）;

注意： 创建 索引 这件 事情 是 非常 低效 的事情 ，尤其 是 当前 表里面 已经是 有很多 数据的时候。
 
另外 ： 不要 去 贸然 创建 索引，别 一个 回车 ，啪嚓 数据库 就挂了。 （这里 给个 忠告 ，我们操作 数据 库 时 一定 要 非常谨慎）、
 

3.删除 索引

 
语法： drop index 索引名字 on 表名 ;

 

注意： 这里 删除 索引 和创建 同理 ，都是 非常 低效 的事情 ，也容易 将 数据库 搞 挂。
 
这里我们 就需要 在创建表 的时候 规划 好 （是否需要创建 索引，删除 索引 等 ） 。
 

补充：
 
使用 SQL 主要还是 使用增删 改查， 虽然SQL 也 支持 条件， 循环， 变量 ，函数等 这些编程 语言普遍的机制 这些 操作 一般 很少 用到 。 （这里我们确实 需要使用 这些逻辑， 一般 会搭配其他的编程语言，比如 ： java）

 

上面 这些索引 操作 一般 面试 不考 ， 下面让我们 学习 一下 面试 常考 的 ， 索引 背后的数据结构。
 

索引背后的数据结构 （面试考点）

索引 背后的 数据 结构 需要能够 加快查找的 速度， 那么 那些 数据机构 能够 加快 查找速度呢？

这里 列举 我们学习 过的 数据结构
 

1. 顺序表

2. 链表

3. 二叉树（二叉搜索树） 【AVL 树 ， 红黑树 （虽然 还没 学 ，这里 这 列举到这里）】

4. 堆 （优先队列）

5. 哈希表

 

1.顺序表 ， 链表

 
这里我们 就要 考虑 使用 那个 才能 加快查询 速度 呢。
 
这里我们 的 顺序表 和 链表 坑定 是不行 的 ，这里我们 的 顺序表 和 链表 都需要遍历 才能 查找。

 

注意： 这里说 的 查找 是 按照 值 查找 ， 而不是 按照 下标 查找 ， 按照 下标 来访问 元素 ，不叫查找 。
 

补充：
 
这里 来 个 问题 ： 为啥 顺序 表 按照 下标访问的速度就快呢 ？
 
其实与 内存 相关 ， 顺序表 是在连续内存空间上，内存支持 随机访问 操作（访问任意地址上的数据，速度都是极快的 并且 每个数据 的访问速度 差不多）。
 
另外：
 
这里 内存 为啥 支持 随机 访问 操作 ，其实 与 内存的硬件 结构（RAM 存储器的 硬件 结构）。
 

顺序表 和 链表 不行 ，那么我们 的 二叉树 （二叉树搜索） 能不能 提高我们的 搜索效率 呢？

2.二叉树（二叉搜索树，AVL树，红黑树）

 
我们 知道 二叉树搜索树 的 特点 ： 左数的 节点 值 都会小于 根节点的 值 ， 右数的节点 值 都会大于 根节点的值 （子树 同样满足 这样的特点）。
 

这里 我们 每次 查找 都会 少掉 一半 ， 这里 就会大大的 加快了我们 的查找 速度 ，这么一看 我们 的 二叉搜索树 是 可以，
 
但是 我们 的 二叉搜索树 的时间复杂度 为 0(N) [ 需要按照 最坏的情况 ，单分子 的情况下 就为O(N) ]，
 
这里我们 最坏的 情况下 我们的 二叉搜索树 就变成 了 一个 链表。
 

这里 我们 为了 避免 二叉搜索树 出现 单分子 的情况 , 这里 就有 了 AVL 树 和 红黑树 ，

 

AVL 树 就 是 要求 比较 严格 的 平衡二叉 树 ， 要求 任意 节点 的左右 子树 高度 差 不超过 1 （不会 出现 单分子 的 情况， 查找速度快了，基本 等于二分查找）。
 
但是 ： 这里我们 数据库 是需要进行 增删 查改的 ，而AVL 树 中，是 不能随意 的 增删查的 ，会 破坏 树 的 结构 ，这里 增删 改 就会 效率 就会 降低。

 

红黑树 ： 要求 比较 宽松 的平衡二叉树 既能 保证 查找 效率 又能 减少 增删 改 的 效率。
 

那么 二叉树 （二叉树搜索树 ，AVL 树，红黑树） 能不能 成为我们 索引 背后的数据结构呢？
 
其实 是 不太 适合 了 ， 为什么呢？

 

这里 当 元素 放入 比较多的 时候，我们树的高度就高了。 （高度对应 着比较 次数）， 对于 数据库 来说 ， 每次 比较 都意味着 磁盘IO 。
 
效率 快了，但 树的 高度 难以控制 （每多 一次 磁盘 IO 都是 很伤 的），所以 不太 适合。
 

二叉树 都不能，那么我们 的哈希表 能不能 作为 索引结构呢？
 

3.哈希表

 
其实 哈希表 也 不太 适合，
 
虽然 哈希表 的查找速度 很快 O(1) ，但 哈希表 只针对 相等 进行 判定 ，不能 对 大于 小于，以及 范围 查找 进行 判定。
 

解释： 哈希表 存储 和 查找 都是 判断 key 值 或 value 值 是否 存在 ， 这里如果 需要 查找 一个 比 key值 大 或 小 的 值 就难以 做到，
 
我们的 哈希表 是通过 哈希 函数来 存储 的 ， 这里 找 大于小于 key 值的 位置 就难以 确定。
 

4.堆

 
最后我们来 看看我们的 堆 ，我们 学习 堆 的时候
 
在学习堆时 我们 是不是 学过 topk 问题， 用在 找 前 k 个 最小 或 最大 （通过 大根堆， 或 小跟堆）。
 
可以看到 我们的 堆 只能 找最小 或 最大 或 范围 查找 ，难以 找到我们 其中的某个 值，所以 堆 也难以胜任索引背后的数据结构。
 

我们 学习 的 数据结构看完 ，既然 没有 一个能 做 索引 的 ， 其实 我 们 最适合 做 索引 的 还是 我们的 树结构，只不过 不是 我们的二叉树 了 ，而是 多叉树搜索树。
 
此时 使用 多叉搜索树， 高度 就 自然就 下降了。
 

多叉搜索树 （索引背后的 男人）

 

 
但是 在数据库 中 使用的这个 多叉 搜索树 ，又不要太一样，是一个 很 特别的 树 成为 B+树 ( 这个 是 数据库索引 中 最常见的 数据结构)。

 

补充： 数据库 有很多 种，每个数据库底层 又支持很多存储引擎（实现了 数据 具体按照啥 结构来存储的程序 ,每个 存储引擎 存储 的 数据结构 可能 都不一样，背后的索引 数据结构 可能 也不同)、
 

这里我们 想要 了解 B+ 树 需要 先 了解 他的 前生 ，B树 （有 的资料上 也 写成 B - 树 ） 注意： 这是B树 的 另外一种 写法 ，而不是 B 减 树。
 
 

B树

 

了解 了 B+树的前身 B树，那么我们 来 了解 一下 B+树，（这里 B+树 只是 对 B 树 做出了 一些 改进）。
 
 

B+树

 

另外 （重点）： 所有 数据 存储 （载荷 ）都是 放到 叶子节点上 ， 非叶子节点 中 只保存 key 即可。 因此 非叶子 整体 占用 的空间 较小 ，甚至 可以 缓存 到内存 中！！！ （这里 一旦 能够 全放 在内存 当中 这个时候 ，磁盘 IO 几乎 就没了）

 

载荷 ：
 

 
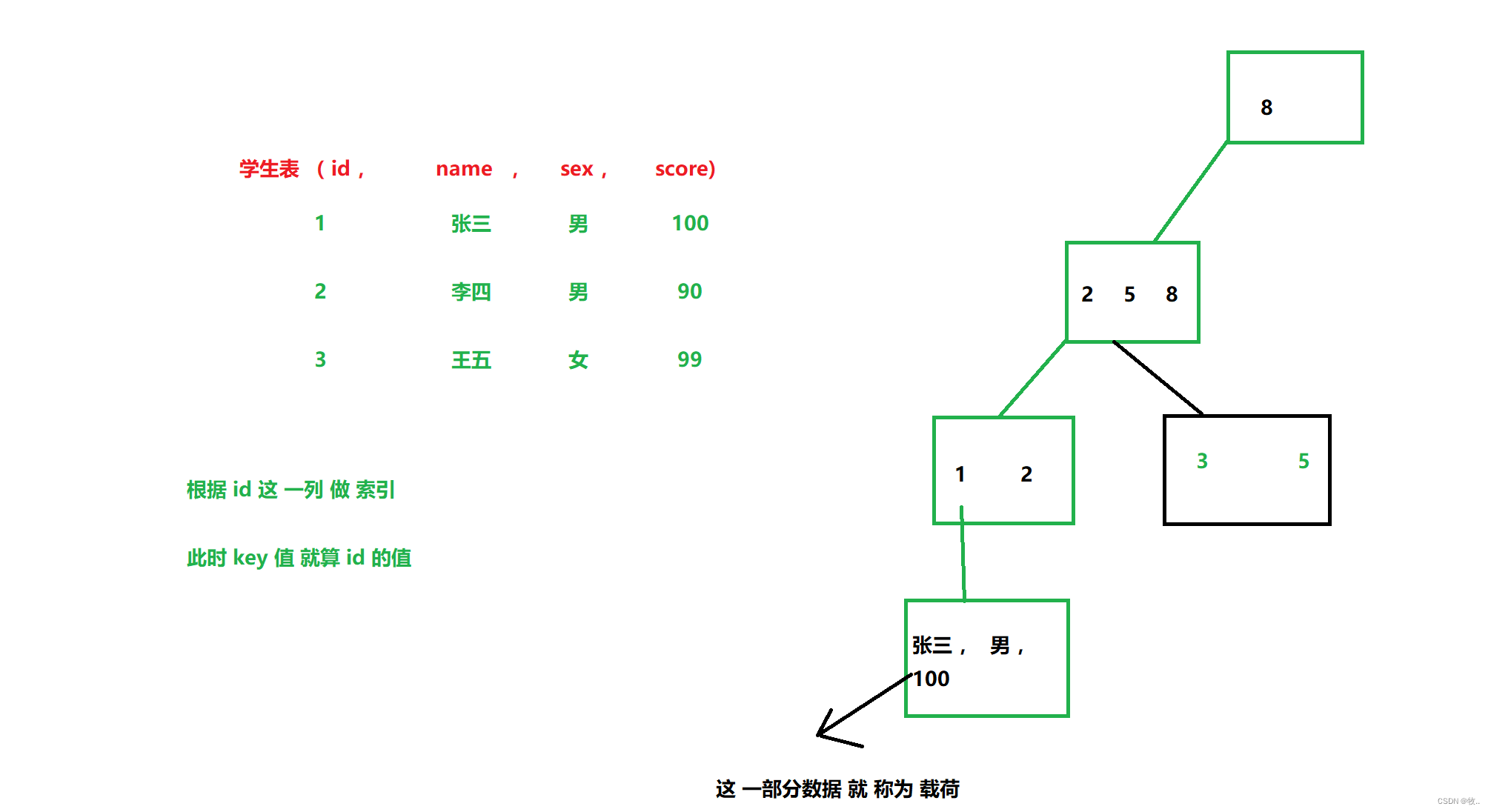
整个数据库存储就是这个载荷（payload）。

 

通过 上面的 几点 可以 发现 B+ 树 为 数据库 索引 量身打造 的 数据结构。
 

这里 B 树 虽然 不太 适合 当 数据库的 索引 ，如何 在其他 场景 下 B+树 就 可能没有 B树 合适 ， 这里就是 你 擅长 这个方面 就不一定 擅长 那个 方面。
 

索引 到此 就完结了
 
那么 面试官问你 下面几道问题 你能 答出来吗？
 

面试 问题

 

题目 一 ： 索引 是干啥的

答： 给 信息 分配 一个 id ，方便 在数据库 快速 查找 该记录。

 

题目二 ： 索引 的 使用 场景

适用于数据库的查询 ，在 海量数据中，使用索引能够 大大减少 查询的时间。

 

题目 三： 索引的 好处去 坏处

索引 带来 的好处 ：提高了 查找的 速度。
 
索引 带来的 坏处 ： 1. 占用 了 更多 的 空间， 2. 拖慢了增 删 改 的 速度。
 

题目 四 ： 索引背后的 数据 结构

上面我们 已经分析 过来， 这里我们 只需要 回答B+树 和 B+树的 4个特点，
 

1. 减少 IO 次数
    
2. 查询结果 最终都会落在 叶子节点上， 还是 减少了 IO次数
    
3. 叶子节点 最后 使用链表相连 方便范围查找
    
4. 所有 数据 存储 （载荷 ）都是 放到 叶子节点上 ， 非叶子节点 中 只保存 key 即可。 因此 非叶子 整体 占用 的空间 较小 ，甚至 可以 缓存 到内存 中！！！ （这里 一旦 能够 全放 在内存 当中 这个时候 ，磁盘 IO 几乎 就没了）

 

这里我们 的索引 就到此 结束 ，下文 我们 将 学习 到 另外一个面试 常考 事务