矩阵分析与应用

一致方程的最小范数解

假设线性方程为：

如图1所示，直线上的所有点都是这个线性方程的解，即通解。但是如果我们要确定一个唯一的解，就必须增加某个约束条件。

比如要求得到的解的范数最小，这样得出的解就称为最小范数解，也称最短距离解。

范数最小等同于该点与原点的距离最小，如图1所示，若要与原点距离最小，则该点与原点的连线垂直与直线。

图1

下面讨论一般情况下线性方程Ax=y的最小范数解，先讨论其通解。

定理：令n*m的矩阵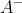是m*n矩阵A的任意一个广义逆矩阵，则

1.齐次方程Ax=0的一个通解为，其中z是n*1的任意向量。                         

 证明：                                                                     

 

即可得

是齐次方程Ax=0的一个通解。

2.非齐次方程Ax=y为一致方程的充分必要条件是：

3.非齐次方程Ax=y的一个通解是：

其中，z为n*1的任意向量。

证明：

即

是非齐次方程Ax=y的一个通解。

那么现在的问题就转变为：是否存在一个与y无关的广义逆矩阵G，能使得解Gy在所有的解中具有最小范数？换言之，该广义逆矩阵G应该满足如下条件：

若满足上式，则称Gy为方程Ax=y的最小范数解，并称广义逆矩阵G为最小范数广义逆矩阵。

考虑矩阵和向量，于是是m阶向量空间的内积，记作，矩阵的伴随矩阵用符号表示，定义为将m阶向量空间的内积等价变换为n阶向量的内积的一个映射，即有：

特别的，若，则称A为自伴随矩阵，显然，自伴随矩阵一定是正方形矩阵，这里的伴随矩阵与逆矩阵中的伴随矩阵的定义有所不同，伴随矩阵有如下性质：

1.

2.

3.

4.（若A为实矩阵）或（A为复矩阵）

定理：Gy是一致方程Ax=y的最小范数解，当且仅当

证明：若Gy是是一致方程Ax=y的一个解，则G必须是满足AGA=A的广义逆矩阵。

一致方程Ax=y的一个通解是:

其中，z为n*1的任意向量。若Gy为最小范数解，则有：

或者

若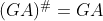，则由AGA=A容易得到：

若，则假设不成立。

继续讨论若具有满行秩m，线性方程Ax=y的最小范数解。

由于A满行秩，故增广矩阵[A,y]的秩与A的秩相同，即线性方程Ax=y是一致方程。存在右伪逆矩阵与之对应的解为：

非一致方程的最小二乘解

考虑非一致方程Ax=y是不存在严格满足方程组的解的，换言之，非一致方程只能有近似解，因此，我们希望寻找严格使得方程两边的误差平方和为最小的解，这一种解称为非一致方程的最小二乘解，具体来说，若用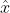代表最小二乘解，则其应该满足：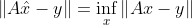

式中，inf代表函数的下确界。

定理：若G为某个矩阵，则是非一致方程Ax=y的最小二乘解，当且仅当满足

或者等价为：

非一致方程的最小二乘解有可能不是唯一的，但是不同的最小二乘解得到的Ax和Ax-y是唯一的。

非一致方程Ax=y的最小二乘解的通解形式为：