线性回归算法原理

最小二乘法解一元线性回归

一、一元线性回归

预备知识

（1）方差

方差是用来衡量样本分散程度的。如果样本全部相等，那么方差为0。方差越小，表示样本越集中， 反正则样本越分散。

方差计算公式如下：

 

python应用：

print(np.var([6, 8, 10, 14, 18], ddof=1))

Numpy里面有var方法可以直接计算方差，ddof参数是贝塞尔(无偏估计)校正系数（Bessel's correction），设置为1，可得样本方差无偏估计量。

 （2）协方差

协方差表示两个变量的总体的变化趋势。如果两个变量的变化趋势一致，也就是说如果其中一个大于 自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变 量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之 间的协方差就是负值。如果两个变量不相关，则协方差为0，变量线性无关不表示一定没有其他相关 性。

协方差公式如下：

 

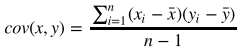
python应用：

print(np.cov([6, 8, 10, 14, 18], [7, 9, 13, 17.5, 18])[0][1])

一元线性回归公式

 

 二、最小二乘法解多元线性回归

多元线性回归公式

 

 写成矩阵形式如下：

 

使用python通过Numpy的矩阵操作就可以完成： 

 Numpy也提供了最小二乘法函数来实现这一过程：

三、多项式回归(不再是直线回归)

上例中，我们假设解释变量和响应变量的关系是线性的。真实情况未必如此。下面我们用多项式回 归，一种特殊的多元线性回归方法，增加了指数项（ 的次数大于1）。现实世界中的曲线关系都是通 过增加多项式实现的，其实现方式和多元线性回归类似。

 案例：

import numpy as np from sklearn.linear_model 
import LinearRegression from sklearn.preprocessing 
import PolynomialFeatures 
X_train = [[6], [8], [10], [14], [18]] 
y_train = [[7], [9], [13], [17.5], [18]] 
X_test = [[6], [8], [11], [16]] 
y_test = [[8], [12], [15], [18]] 
regressor = LinearRegression() 
regressor.fit(X_train, y_train) 
xx = np.linspace(0, 26, 100) 
yy = regressor.predict(xx.reshape(xx.shape[0], 1)) 
plt = runplt() 
plt.plot(X_train, y_train, 'k.') 
plt.plot(xx, yy) 
quadratic_featurizer = PolynomialFeatures(degree=2) 
X_train_quadratic = quadratic_featurizer.fit_transform(X_train) 
X_test_quadratic = quadratic_featurizer.transform(X_test) 
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train) 
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1)) 
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-') 
plt.show() 
print(X_train) 
print(X_train_quadratic) 
print(X_test) 
print(X_test_quadratic) 
print('一元线性回归 r-squared', regressor.score(X_test, y_test)) 
print('二次回归 r-squared', regressor_quadratic.score(X_test_quadratic, y_ test))

四、优化

前面计算可以理解为是最小化成本函数，成本函数计算如下：

 

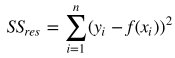
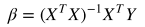
 这里 是解释变量矩阵，当变量很多（上万个）的时候， 计算量会非常大。另外，如果 的 行列式为0，即奇异矩阵，那么就无法求逆矩阵了。这里我们介绍另一种参数估计的方法，梯度下降 法（gradient descent）。拟合的目标并没有变，我们还是用成本函数最小化来进行参数估计。

梯度下降法拟合模型

随机梯度下降（Stochastic gradient descent，SGD）

下面我们用scikit-learn的SGDRegressor类来计算模型参数。它可以通过优化不同的成本函数来拟合 线性模型，默认成本函数为残差平方和。

残差平方 和构成的成本函数是凸函数，所以梯度下降法可以找到全局最小值。

案例：

import numpy as np 
from sklearn.datasets import load_boston 
from sklearn.linear_model import SGDRegressor 
from sklearn.cross_validation import cross_val_score 
from sklearn.preprocessing import StandardScaler 
from sklearn.cross_validation import train_test_split 
data = load_boston() 
X_train, X_test, y_train, y_test = train_test_split(data.data, data.targe t)
X_scaler = StandardScaler() 
y_scaler = StandardScaler() 
X_train = X_scaler.fit_transform(X_train) 
y_train = y_scaler.fit_transform(y_train) 
X_test = X_scaler.transform(X_test) 
y_test = y_scaler.transform(y_test)
regressor = SGDRegressor(loss='squared_loss') 
scores = cross_val_score(regressor, X_train, y_train, cv=5) 
print('交叉验证R方值:', scores) 
print('交叉验证R方均值:', np.mean(scores)) 
regressor.fit_transform(X_train, y_train) 
print('测试集R方值:', regressor.score(X_test, y_test))

Ridge 回归

Ridge 回归通过对系数的大小施加惩罚来解决 普通最小二乘法 的一些问题。 岭系数最小化的是带罚项的残差平 方和