1 引入

1.1 题目

  2017：指针生成器网络 (Get to the point: Summarization with pointer-generator networks)

1.2 摘要

  神经序列到序列模型为抽象文本摘要提供了一种可行的新方法，这意味着它们不限于简单地从原始文本中选择和重新排列段落。然而，这些模型有以下两个缺点：
  1）有可能不准确的复制事实细节；
  2）倾向于复制本身。
  本文以两种正交方式提出了一种用以增强标准序列到序列模型的架构。
  1）使用混合指针生成器网络通过指针从源文本复制单词。这有助于准确复制信息，同时保留通过生成器产生新词的能力；
  2）使用覆盖 (Coverage) 来跟踪总结的内容，并在一定程度上限制重复。
  实验讲在CNN/Daily Mail上进行。

1.3 代码

  Tensorflow：https://github.com/abisee/pointer-generator
  Torch：https://github.com/atulkum/pointer_summarizer

1.4 Bib

@article{See:2017:get,
author		=	{Abigail See and Peter J Liu and Christopher D Manning},
title		=	{Get to the point: Summarization with pointer-generator networks},
journal		=	{arXiv:1704.04368},
year		=	{2017}
}
1
2
3
4
5
6

2 模型

  本节将描述1）基准序列到序列模型，2）指针生成器模型，以及3）能够添加到以上任意一个模型的覆盖机制。

2.1 序列到序列注意力模型

  图2展示了基准的序列到序列模型。文章的token $w_i$将传递给编码器，一个单层双向LSTM，用以生成编码器隐藏状态$h_i$。在每一个时间步$t$，解码器，一个单层单向LSTM接收前一个词的词嵌入 (训练时是参考摘要的前一个词；测试时是解码器发出的前一个词)，并获取解码器状态$s_t$。

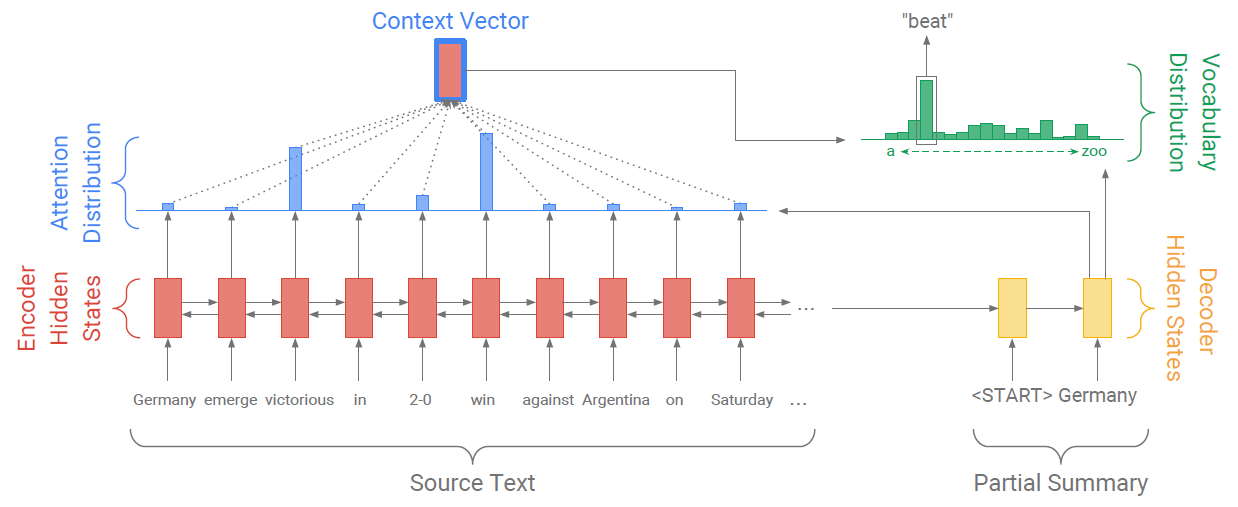
  图2：指针生成器模型。对于每个解码器时间步长，计算生成概率$p_{gen}\in [0,1]$，它对从词汇表生成单词的概率与从源文本复制单词的概率进行加权。词汇表的分布与注意力的分布的加权和将作为最终的分布。注意诸如2-0之类的词汇外文章单词将包含在最终分布中。

  Bahdanau提出的注意力分布计算如下：
e i t = v T tanh ⁡ ( W h h i + W s s t + b attn ) a t = softmax ( e t ) (1–2) \tag{1--2}

eit​at​==​vTtanh(Wh​hi​+Ws​st​+battn​)softmax(et)​(1–2)其中$v,W_h,W_s,b_{\text{attn}}$是习得参数。注意力分布可以看作是所有源单词的概率分布，其指示了解码器在哪里寻找下一个单词。接下来，注意力分布的加权和将作为上下文向量$h_t^{\ast }$：
$$h_t^{\ast }=\sum _i{a}_i^t{h}_i\text{\hspace{1em}(3)}$$  上下文向量可以看作是从源中读取内容的固定大小表示，与解码器状态$s_t$连接，并传递给两个线性层，以生成词汇表分布$P_{\text{vocab}}$：
$$P_{\text{vocab}}=\text{softmax}(V^{\prime }(V[s_t,h_t^{\ast }]+b)+b^{\prime })\text{\hspace{1em}(4)}$$其中$V,V^{\prime },b,b^{\prime }$是习得参数。$P_{\text{vocab}}$是关于词汇表中所有单词的概率分布，可以提供预测单词$w$的最终分布：
$$P(w)=P_{\text{vocab}}(w)\text{\hspace{1em}(5)}$$在训练阶段，时间步$t$的损失是目标单词$w_t^{\ast }$在当前时间步下对数似然的负数：
$${\text{loss}}_t=-\log P(w_t^{\ast })\text{\hspace{1em}(6)}$$以及整个时间步的总体损失为：
$$\text{loss}=\frac{1}{T}\sum _{t=0}^T{\text{loss}}_t\text{\hspace{1em}(7)}$$

2.2 指针生成网络

  指针生成网络是基准网络与指针网络的混合，它允许通过指针复制单词，同时可以从固定词汇表生成单词。在前述章节中，已经获取了注意力分布$a^t$和上下文向量$h_t^{\ast }$。接下来，每个时间步$t$的生成概率$p_{\text{gen}}$将通过$h_t^{\ast }$、解码器状态$s_t$，以及解码器输入$x_t$获得：
$$p_{\text{gen}}=\sigma (w_{h^{\ast }}^T{h}_t^{\ast }+w_s^T{s}_t+w_x^T{x}_t+b\text{ptr})\text{\hspace{1em}(8)}$$其中$w_{h^{\ast }},w_s,w_x,b\text{ptr}$是习得参数，$\sigma$是sigmoid函数。接下来$p_{\text{gen}}$被用于软转换，即从由$p_{\text{vocab}}$采样的词汇表生成单词，或者是从通过采样注意力分布$a_t$得到的输入序列中拷贝单词。对于每个文档，让扩展词汇表表示词汇表的并集，以及出现在源文档中的所有单词。基于扩展词汇表，可以获取如下概率分布：
$$P(w)=p_{\text{gen}}{P}_{\text{vocab}}(w)+(1-p_{\text{gen}})\sum _{i:w_i=w}{a}_i^t。\text{\hspace{1em}(9)}$$注意，如果$w$是一个超纲单词 (Out-of-vocabulary, OOV)，$P_{\text{vocab}}(w)$是输出为0；而如果$w$如果没有出现在源文档中，${\sum }_{i:w_i=w}{a}_i^t=0$。生成OOV词是指针生成器模型的主要优势之一。相比之下，基线等模型仅限于预设的词汇表。
  此时，损失函数为使用公式9计算概率分布的公式6和7。

2.3 覆盖机制

  重复是序列到序列的一个常见问题，尤其是在如图1所示的多序列文本生成中。我们使用适应的覆盖机制来处理这个问题。在覆盖模型中，我们生成一个覆盖向量$c^t$，其是先前所有解码器时间步的注意力分布之和：
$$c^t=\sum _{t^{\prime }=0}^{t-1}{a}^t\text{\hspace{1em}(10)}$$直观上$c^t$是一个覆盖源文档多有单词的未标准化分布，其表示到目前为止这些词从注意力机制中获得的覆盖程度。注意$c^0$是一个零向量，因此在时间步0没有源文档被覆盖。

图1：三个摘要总结模型在新闻文章上输出的对比。基线模型会出现事实错误、无意义的句子并与 OOV单词muhammadu buhari冲突。指针生成器模型准确却会重复的。 覆盖机制可以消除这些重复，使得最后的总结由几个片段组成。

 
  覆盖向量被作为注意力机制的额外输入，因此公式1被重写为：
$$e_i^t=v^T\tanh (W_h{h}_i+W_s{s}_t+w_c{c}_i^t+b\text{attn})\text{\hspace{1em}(11)}$$其中$w_c$是与$v$同形的习得向量。该机制使得注意力机制的先前决策可以影响到其当前决策。这可以轻松地使得注意力不会过多地关注同一个区域，因此避免产生重复的文本。
  
  我们发现有必要额外定义覆盖损失以惩罚重复访问相同位置的情况：
$${\text{covloss}}_t=\sum _i\min (a_i^t,c_i^t)\text{\hspace{1em}(12)}$$注意覆盖损失是有界限的，即${\text{covloss}}_t\le {\sum }_i{a}_i^t=1$。公式12机器翻译 (Machine translation, MT) 中使用的覆盖损失不同。在MT中，我们假设应该有一个大致一比一的翻译比例，因此如果最终的覆盖向量大于或小于 1，则会受到惩罚。
  最终的损失函数更加灵活：因为摘要不需要统一覆盖，所以只惩罚每个注意力分布和迄今为止的覆盖之间的重叠——防止重复注意力：
$${\text{loss}}_t=-\log P(w_t^{\ast })+\lambda \sum _i\min (a_i^t,c_i^t)\text{\hspace{1em}(13)}$$