极验深知v2分析

案例地址：geetest.com/Register
案例内容：分析极验登录时深知检测V2提交的Request Payload信息。

文章内容仅作学习参考，如有侵权请联系作者进行删除

---

---

接口分析

POST请求

加密Payload：

---

参数定位

长话短说，通过XHR断点。

往回走5步就可以看到参数生成的位置。

根据调试信息和接口中的值对比，发现e = DWYi[ymDv(1137)](l)是payload的其中一部分。

继续调试，发现代码：e + h[AUJ_(1173)]

结合调试信息得出结论：payload = DWYi[ymDv(1137)](l) + h[AUJ_(1173)]

---

h[AUJ_(1173)]

经测试，h是动态的，其中的aeskey和rsa的值不固定。

再次分析源码，可知 h = o[AUJ_(1156)]()

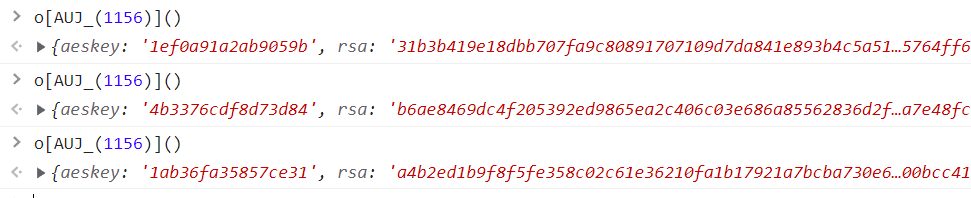
继续调试，AUJ_(1156) = ‘LpFU’

双击点进去，找到对应的方法。

把这个文件内容在 Lxtools 中解混淆一下,变量名还原。

复制到本地格式化后的整体代码结构如下：

发现都是自执行的方法，手动处理后可以改成如下所示：

然后根据报错把环境补上，比如出现的这些

补完之后再次运行，会返回MlHc。 然后修改下代码，让其返回 LkEB['prototype'].LpFU()。

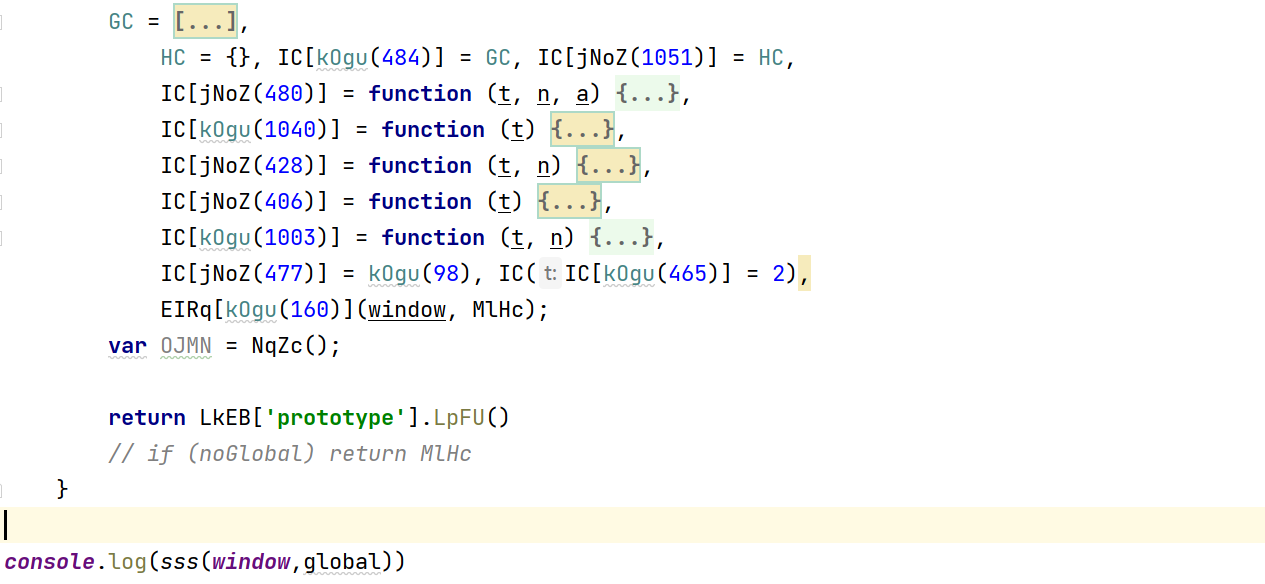
运行测试，成功打印了 o[AUJ_(1156)]()，从中提出rsa参数即可。

---

DWYi[ymDv(1137)](l)

先查看各项含义，其中 l 是EbF_[ymDv(409)](e, h[ymDv(1194)])，调用方法为DWYi['tc_t']

---

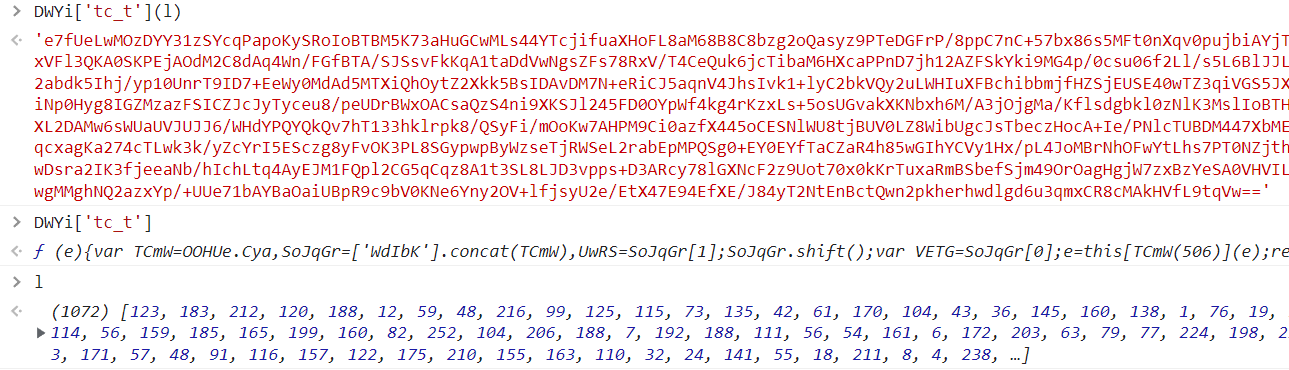
先看 l

可知此处的 aeskey 是从我们第一段分析分析的 o[AUJ_(1156)]() 对象中提取的。

此处的e 中包括了操作id、行为轨迹，以及未知参数。

EbF_[ymDv(409)]是对应的encrypt加密方法。在本地中可看到由JOOO返回，JOOO在EbF_中。

那可以直接使用 EbF_.encrypt()来调用加密方法。

即：EbF_.encrypt(e, h[ymDv(1194)])

本地调用，成功生成 l 。

---

调用tc_t

有了l 之后，我们在补的JS中直接调用DWYi.tc_t(l) 即可。

总体流程：

// 注册 _asekey_rsa 
_asekey_rsa = LkEB['prototype'].LpFU()
rsa = _asekey_rsa.rsa
aeskey = _asekey_rsa.aeskey
// 生成 l
var l = EbF_.encrypt(e,aeskey)
// 加密后拼接
return DWYi.tc_t(l)+rsa
1
2
3
4
5
6
7
8

打印结果：

---

总结

主要内容是流程分析和对混淆代码的处理和调用。

文章内容相对深知检测来说只是皮毛，只分析了Payload参数，深层的检测分析任重而道远。

本文辅助代码在公众号《Pythonlx》回复 shenzhi 领取。