leetcode94 -- 二叉树的中序遍历

一、问题描述

给定一个二叉树的根节点root ，返回 它的中序遍历 。

示例 1：

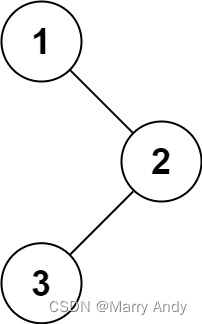
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

二、解决问题

法一：递归

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();

        inOrder(root, res);
        return res;
    }
    public void inOrder(TreeNode root, List res){
        if(root == null)
            return;

        inOrder(root.left, res);
        res.add(root.val);
        inOrder(root.right, res);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 时间复杂度：O(n)
  （其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。）
• 空间复杂度：O(n)
  （空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。）

法二：非递归

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();

        Stack<TreeNode> stack = new Stack<TreeNode>();
        

        while(root != null || !stack.isEmpty()){
            while(root != null){
                stack.push(root);
                root = root.left;
            }   
            root = stack.pop();
            res.add(root.val);
            root = root.right;
        }
        return res;         
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

• 时间复杂度：O(n)
  （其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。）
• 空间复杂度：O(n)
  （空间复杂度取决于栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。）

法三：Morris 中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
       List<Integer> ans=new LinkedList<>();
        while(root!=null){
            //没有左子树，直接访问该节点，再访问右子树
            if(root.left==null){
                ans.add(root.val);
                root=root.right;
            }else{
            //有左子树，找前驱节点，判断是第一次访问还是第二次访问
                TreeNode pre=root.left;
                while(pre.right!=null&&pre.right!=root)
                    pre=pre.right;
                //是第一次访问，访问左子树
                if(pre.right==null){
                    pre.right=root;
                    root=root.left;
                }
                //第二次访问了，那么应当消除链接
                //该节点访问完了，接下来应该访问其右子树
                else{
                    pre.right=null;
                    ans.add(root.val);
                    root=root.right;
                }
            }
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

• 时间复杂度：O(n)
  （其中 n 为二叉搜索树的节点个数。Morris 遍历中每个节点会被访问两次，因此总时间复杂度为 O(2n)=O(n)。）
• 空间复杂度：O(1)

参考：https://leetcode.cn/problems/binary-tree-inorder-traversal/solution/