• Chapter 6 提升

    1 随机森林的特点

    随机森林的决策树分别采样建立，相对独立。

    ps:由弱分类器——>强分类器方法：样本加权、分类器加权。

    样本加权：例如对于某个样本进行分类，会存在分类错误的样本，对此增大其权值。

    分类器加权：对于误分类率低的弱分类器，我们在最终结果中给予更高的权重。

    权值指的是预测值。

    2 提升

    2.1 提升

    提升——提升是一个机器学习技术，可以用于回归和分类问题，它每一步产生一个弱预测模型（如决策树），并加权累加到总模型中。

    梯度提升——如果每一步的弱预测模型生成都是依据损失函数的梯度方向，则称之为梯度提升。

    提升的理论意义——如果一个问题存在弱分类器，则可以通过提升的方法得到强分类器。

    2.2 梯度提升算法

    梯度提升算法首先给定一个目标损失函数（我们自己根据实际问题给定的，与提升无关），它的定义域是所有可行的弱函数集合（基函数）。提升算法通过迭代选择一个负梯度方向上的基函数来逐渐逼近局部极小值。这种在函数域的梯度提升观点对机器学习的很多领域有深刻影响。

    2.3 提升算法

    给定输入向量x和输出变量y组成的若干训练样本(x1,y1)，(x2,y2),……(xn,yn)，目标是找到近似函数\widehat{F}(\overrightarrow{x})，使得损失函数L(y,F(x))的损失值最小。

    损失函数L(y,F(x))的典型定义为：L(y,F(\overrightarrow{x}))=\frac{1}{2}(y-F(\overrightarrow{x}))^{2}或L(y,F(\overrightarrow{x}))=|y-F(\overrightarrow{x})|

    假定最优函数为F^{*}(\overrightarrow{x})，即：F^{*}(\overrightarrow{x})=\underset{F}{arg min}E_{(x,y)}[L(y,F(\overrightarrow{x}))]

    假定F(x)是一族基函数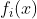f_{i}(x)的加权和F(\overrightarrow{x})=\sum_{i=1}^{M}\gamma _{i}f_{i}(x)+const

    证明：中位数是绝对最小最优解。

    给定样本x1,x2,……,xn，计算\mu ^{*}=\underset{\mu }{arg min}\sum_{i=1}^{n}|x_{i}-\mu |

    J(\mu )=\sum_{i=1}^{n}|x_{i}-\mu |=\sum_{i=1}^{k}(\mu -x_{i})+\sum_{i=k+1}^{n}(x_{i}-\mu )

    求偏导：\frac{\partial J(\mu )}{\partial \mu }=\sum_{i=1}^{k}(1)+\sum_{i=k+1}^{n}(-1)，令其等于0。

    得到前k个样本数目与后n-k个样本数目相同，即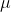\mu为中位数。

    提升算法推导：

    梯度近似：

    提升算法：
     

    3 梯度提升决策树GBDT

     3.1 定义

     3.2 总结

    4 目标函数

     4.1 二阶导信息

    4.2 目标函数的计算

    4.3 目标函数的简化

    5 Adaboost

    5.1 Adaboost定义

    设训练数据集T=\left \{ (x_{1},y_{1}),(x_{2},y_{2})...(x_{N},y_{N})\right \}

    初始化训练数据的权值分布：D_{1}=(w_{11},w_{12}...w_{1i}...,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,...,N,

    5.2 Adaboost算法

     

     5.3 举例说明

    m=1：

    序号123456789x
    X0123456789
    Y111-1-1-1111

    -1

     权值分布为D1的训练数据上，阈值v取2.5时误差率最低，故基本分类器为G_{1}(x)=\left\{\begin{matrix} 1 & x<2.5\\ -1 & x>2.5 \end{matrix}\right.

    我们可以看到x=6、7、8时数据存在误差，所以误差率为0.3，即e1=0.3=3*0.1。

    代入G1的系数：\alpha _{1}=\frac{1}{2}log\frac{1-e_{1}}{e_{1}}=0.4236

    ∴f_{1}(x)=0.4236*G_{1}(x)

    分类器sign(f_{1}(x))在训练数据集上有3个误分类点。

    计算权值D_{2}=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)

    可以看到误差的点x=6、7、8的权值变大。为下个基本分类器所用，即m=2时。

    m=2:

    X0123456789
    Y111-1-1-1111-1
    w0.07150.07150.07150.07150.07150.07150.16660.16660.16660.0715

    权值分布为D2的训练数据上，阈值v取8.5时误差率最低，故基本分类器为G_{2}(x)=\left\{\begin{matrix} 1 & x<8.5\\ -1 & x>8.5 \end{matrix}\right.

    可以看到x=3、4、5存在误差，所以误差率为0.2143，即e2=0.2143=0.0715*3

    代入G1的系数\alpha _{2}=\frac{1}{2}log\frac{1-e_{2}}{e_{2}}=0.6496

    f_{2}(x)=0.4236*G_{1}(x)+0.6496G_{2}(x)

    分类器sign(f_{2}(x))在训练数据集上有3个误分类点。 

     计算权值D3=(0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455)

    可以看到x=3、4、5的权值变大。为下个基本分类器所用，即m=3时。

    m=3依次类推……

    5.4  权值和错误率的关键解释

  • 相关阅读:
    Vue守卫详解
    【前段基础入门之】=＞CSS 的常用属性
    GitLab升级16.5.0后访问提示502
    Spring简介
    阿桑的感慨
    被一位读者赶超，手摸手 Docker 部署 ELK Stack
    ESP32C3 LED PWM使用和ESP32差异说明
    解密IP分片与重组：数据传输中的关键技术
    Taurus.MVC WebMVC 入门开发教程7：部分视图和页面片段（结束篇）
    kafka学习笔记
  • 原文地址：https://blog.csdn.net/qwertyuiop0208/article/details/126005370