-
矩阵分析与应用
广义逆矩阵的定义与性质
考虑
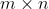 阶的一般矩阵A,其秩k小于或等于
阶的一般矩阵A,其秩k小于或等于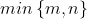 。
。我们的问题是:是否存在某种合适意义下的逆矩阵,使得线性方程组
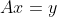 的解可以用这种逆矩阵表示?
的解可以用这种逆矩阵表示?定义1:有线性方程
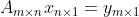 ,若矩阵A的行之间存在的线性关系也存在于向量y的对应元素中,则该方程组称为一致方程(即至少存在一个解能够严格满足该方程组)。
,若矩阵A的行之间存在的线性关系也存在于向量y的对应元素中,则该方程组称为一致方程(即至少存在一个解能够严格满足该方程组)。如:
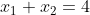
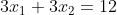
矩阵A的第二行是第一行的3倍,向量y的第二个元素也是第一个元素的3倍。
定义2:仅当线性方程组为一致方程时。这一线性方程组方可求解。
定义3:当且仅当增广矩阵
![\left [ A,y \right ]](https://1000bd.com/contentImg/2022/07/31/041018581.gif) 的秩等于矩阵
的秩等于矩阵 的值,即
的值,即![rank([A,y])=rank(A)](https://1000bd.com/contentImg/2022/07/31/041020477.gif) 时,线性方程
时,线性方程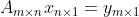 是一致方程。
是一致方程。定义4:A是一个m*n的矩阵,具有任意秩,矩阵A的广义逆矩阵是一个n*m的矩阵G,并当
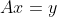 为一致方程时,使得
为一致方程时,使得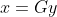 是线性方程
是线性方程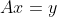 的解。
的解。定义5:当且仅当
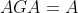 时,一致方程
时,一致方程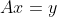 对于
对于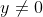 有解
有解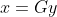 。
。定义6:方程
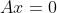 的解与矩阵A的任意行正交,并且线性无关。
的解与矩阵A的任意行正交,并且线性无关。m*n矩阵A的广义逆矩阵G用符号
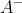 表示,即
表示,即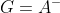 。
。广义逆矩阵有着以下重要性质。
1.
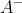 存在
存在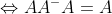
2.
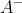 存在
存在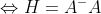 为幂等矩阵(即
为幂等矩阵(即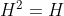 )且
)且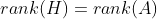
3.
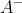 存在
存在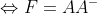 为幂等矩阵(即
为幂等矩阵(即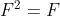 )且
)且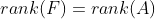
定义:m*n的矩阵A的广义逆矩阵是一个满足
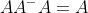 的n*m的矩阵
的n*m的矩阵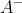 。
。定义:m*n的矩阵A的广义逆矩阵是满足下列条件之一的n*m矩阵
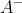 :
:1.
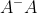 为幂等矩阵,且
为幂等矩阵,且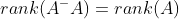
2.
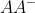 为幂等矩阵,且
为幂等矩阵,且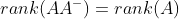
逆矩阵,左逆矩阵,右逆矩阵都可以视为广义逆矩阵的一个特例。
1.逆矩阵
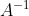 满足
满足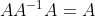
2.左逆矩阵L满足
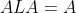 ,因为
,因为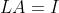
3.右逆矩阵R满足
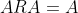 ,因为
,因为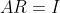
广义逆矩阵的计算
满秩分解:矩阵
 具有秩r,若A=FG,其中
具有秩r,若A=FG,其中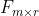 的秩为r(满列秩矩阵),且
的秩为r(满列秩矩阵),且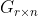 的秩也为r(满行秩矩阵),则称A=FG为矩阵A的满秩分解。
的秩也为r(满行秩矩阵),则称A=FG为矩阵A的满秩分解。命题:一个秩为r的m*n矩阵A可以分解为
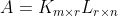
其中K和L分别具有满列秩和满行秩。
证明:存在m*m的非奇异矩阵P和n*n非奇异矩阵Q使得:
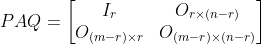
或等价为:
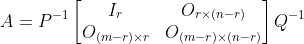
将逆矩阵
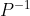 和
和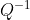 分块为:
分块为:![P^{-1}=[K_{m\times r},W_{m\times (n-r)}]](https://1000bd.com/contentImg/2022/07/31/041112319.gif)

于是,有:![A=[K,W]\begin{bmatrix} I_{r} &O \\ O& O \end{bmatrix}\begin{bmatrix} L\\Z \end{bmatrix}=[K,O]\begin{bmatrix} L\\Z \end{bmatrix}=K_{m\times r}L_{r\times n}](https://1000bd.com/contentImg/2022/07/31/041113942.gif)
由于P是非奇异的,因此
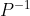 也是非奇异的,即
也是非奇异的,即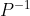 的列是线性无关的,特别地,矩阵K的r列线性无关,固有rank(K)=r,即K具有满列秩。类似的,L具有满行秩。
的列是线性无关的,特别地,矩阵K的r列线性无关,固有rank(K)=r,即K具有满列秩。类似的,L具有满行秩。矩阵的满秩分解算法:
步骤1:利用行初等变换将矩阵A化为阶梯型。
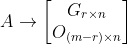
步骤2 对单位矩阵执行逆行初等变换,得到逆矩阵
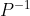
步骤3 利用逆矩阵
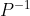 的前r列构造矩阵F
的前r列构造矩阵F步骤4 书写满秩分解结果A=FG
引理:若矩阵
 具有秩r,且其满秩分解为A=FG,其中
具有秩r,且其满秩分解为A=FG,其中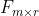 为满列秩,
为满列秩,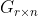 为满行秩,则
为满行秩,则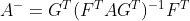
是A的一个广义逆矩阵。
证明如下:
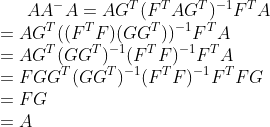
广义逆矩阵的计算总结如下:
1.计算矩阵的满秩分解A=FG
2.求广义逆矩阵
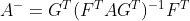
-
相关阅读:
3种python查看安装的所有库,然后将他们组合成一个pip命令
冶金行业渠道商经销管理系统统一渠道商监管,提高企业管理效率
逆向分析练习三(最长公共前缀)
MyBatis的缓存
Android 保存图片并刷新相册(无需权限)
第九章(1):循环神经网络与pytorch示例(RNN实现股价预测)
Web缓存
Ansible-部署haproxy高可用
Pandas数据分析13——数据框合并(实现excel的Vlookup功能)
Linux常用命令——convertquota命令
- 原文地址:https://blog.csdn.net/weixin_46007132/article/details/126010824