剑指 Offer 07. 重建二叉树

剑指 Offer 07. 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

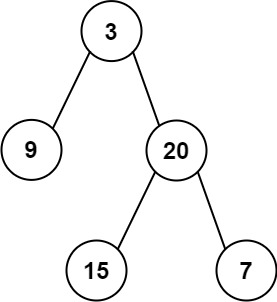
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
1
2

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]
1
2

思路分析

首先要知道遍历后的数组都有什么样的特点

• 在前序遍历序列中,第一个元素为树的根节点
• 在中序遍历序列中,根节点的左边为左子树，根节点的右边为右子树

根据上面的理论知识可以清楚本题的解题策略，就是以 前序数组的第一个元素【根节点】为切割点，先切中序数组，根据中序数组，反过来在切前序数组。一层一层切下去，每次前序数组的第一个元素就是节点元素。

前序遍历的第一个元素就是他的头节点。知道了头节点，我们可以在中序遍历中找到头节点的位置index。通过index我们就可以求出来左子树在数组中的长度： index - inorder_start。（inorder_start是中序遍历的起点）。

1. 获取树的头节点int root_val = preorder[preorder_start] (preorder_start是前序遍历的起始值)。然后我们直接构建二叉树 的根节点 TreeNode* root = new TreeNode(root_val)

2. 构建左树：root->left 我们知道该二叉树的左子树的长度为 left_length = index - inorder_start

   所以我们可以推出二叉树的左子树在前序遍历的位置是 [preorder_start+1,preorder_start+left_length]。
   同理：二叉树的左子树在中序遍历的位置是[inorder_start, index - 1]。

3. 构建右树：root->right
   二叉树的右子树在前序遍历的位置是 [preorder_start+left_length+1,preorder_end]。
   同理：二叉树右子树在中序遍历的位置是[index + 1 , inorder_end]。
   代码如下：👇👇👇👇

class Solution {
public:
    //递归代码
    TreeNode* buildcore(const vector<int>& preorder, const vector<int>& inorder, int preorder_start, int preorder_end, int inorder_start, int inorder_end)
    {
        if(preorder_start>preorder_end||inorder_start>inorder_end)
        {
            return nullptr;
        }
        //前序遍历的第一个数字是根节点的值
        int root_val = preorder[preorder_start];
        TreeNode* root = new TreeNode(root_val);
        //区间里只有一个值,返回
        if(preorder_start == preorder_end)
        {
            return root;
        }
        //中序遍历找到根节点的位置
        int index = 0;
        //可以等于，在范围内
        while(index <= inorder_end && inorder[index] != root_val)
        {
            index++;
        }
        //如果index大于inorder_end，说明没找到，报错，题目所给的意思是肯定能找到，所以这里就不判断了。
        //左右子树区间大小。
        int left_length = index - inorder_start;

        root->left = buildcore(preorder,inorder,preorder_start+1,preorder_start+left_length,inorder_start,index-1);
        root->right = buildcore(preorder,inorder,preorder_start+left_length+1,preorder_end,index+1,inorder_end);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int n = preorder.size();
        if(n==0)
        {
            return 0;
        }
        return buildcore(preorder,inorder,0,n-1,0,n-1);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

106. 从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

该题与上题类似，可以使用相同的解法递归解决。

思路分析

• 在后序遍历序列中,最后一个元素为树的根节点

• 在中序遍历序列中,根节点的左边为左子树，根节点的右边为右子树

以 后序数组的最后一个元素【根节点】为切割点，先切中序数组，根据中序数组，反过来在切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

class Solution {
public:
    TreeNode* buildcore(const vector<int>& inorder, const vector<int>& postorder, int inorder_start, int inorder_end, int post_start, int post_end)
    {
        if(inorder_start>inorder_end||post_start>post_end)
        {
            return nullptr;
        }
        //后序遍历的最后一个值是根节点
        int root_val = postorder[post_end];
        TreeNode* root = new TreeNode(root_val);
        //遍历找根节点在中序遍历的的位置
        int index = 0;
        for(index = 0; index<= inorder_end; index++)
        {
            if(inorder[index] == root_val)
            {
                break;
            }
        }
        //计算左子树的长度
        int left_length = index - inorder_start;
        //构建左子树
        root->left = buildcore(inorder,postorder,inorder_start,index-1,post_start,post_start+left_length-1);
        //构建右子树
        root->right = buildcore(inorder,postorder,index+1,inorder_end,post_start+left_length,post_end-1);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
    {
        int n = inorder.size();
        if(n==0)
        {
            return nullptr;
        }
        return buildcore(inorder,postorder,0,n-1,0,n-1);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38