KMP 算法

引入：

KMP 算法是一个快速查找匹配串的算法，它的作用其实就是本题问题：**如何快速在「原字符串」中找到「匹配字符串」。**上述的朴素解法，不考虑剪枝的话复杂度是 O(m * n)的，而 KMP 算法的复杂度为 O(m + n)。

KMP 之所以能够在 O(m + n) 复杂度内完成查找，是因为其能在「非完全匹配」的过程中提取到有效信息进行复用，以减少「重复匹配」的消耗。

原理：

原理详情请看参考链接里面的，一定会给你讲懂的。

匹配过程：

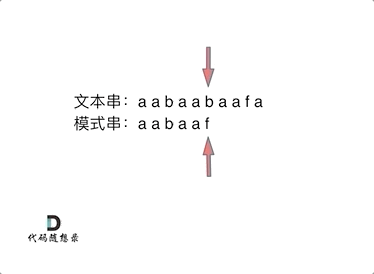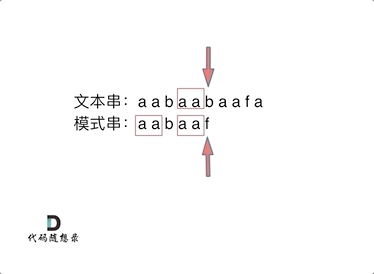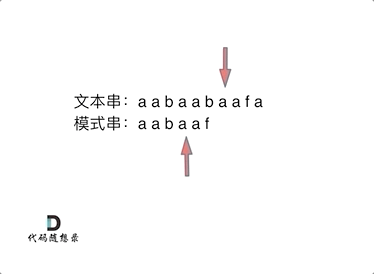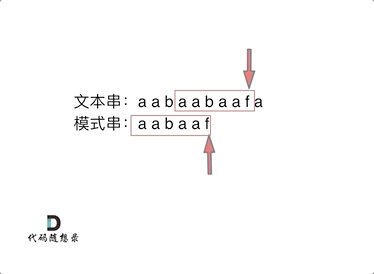
计算前缀表：

有些会在前缀表上面做一些小规定。

最原始的样子：

使用next数组来匹配：

构造next数组：

如何编程快速求得next数组。其实，求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度

代码实现:

private void getNext(int[] next, String s) {
    int j = 0;//默认next的值是0;
    next[0] = j;//默认next第一位下标是0;
    for (int i = 1; i < s.length(); i++) {//默认next从下标1开始慢慢修改.
        while (j > 0 && s.charAt(j) != s.charAt(i))//只要不匹配,就回退.
            j = next[j - 1];
        if (s.charAt(j) == s.charAt(i))//相等就往后面移动
            j++;
        next[i] = j;//记录当前j的值作为next的值.
    }
}
1
2
3
4
5
6
7
8
9
10
11

模板：

通过28. 实现 strStr() - 力扣（LeetCode）来了解kmp的具体使用.

class Solution {
    //前缀表（不减一, 也不后移）Java实现
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0) return 0;
        int[] next = new int[needle.length()];
        getNext(next, needle);//构造模式串的next数组.

        int j = 0;
        for (int i = 0; i < haystack.length(); i++) {//类似于getNext中字符串匹配的过程
            while (j > 0 && needle.charAt(j) != haystack.charAt(i))//不匹配就回退.
                j = next[j - 1];
            if (needle.charAt(j) == haystack.charAt(i))//相等就后面移动
                j++;
            if (j == needle.length())//移动至模式串尾部就返回index;
                return i - needle.length() + 1;
        }
        return -1;
    }
    private void getNext(int[] next, String s) {
        int j = 0;//默认next的值是0;
        next[0] = j;//默认next第一位下标是0;
        for (int i = 1; i < s.length(); i++) {//默认next从下标1开始慢慢修改.
            while (j > 0 && s.charAt(j) != s.charAt(i))//只要不匹配,就回退.
                j = next[j - 1];
            if (s.charAt(j) == s.charAt(i))//相等就往后面移动
                j++;
            next[i] = j;//记录当前j的值作为next的值.
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

题目实战：

实现 strStr()

28. 实现 strStr() - 力扣（LeetCode）

略!

重复的子字符串

459. 重复的子字符串 - 力扣（LeetCode）

最长相等前后缀的长度为：next[len - 1] 。（这里的next数组是不有做处理的样子）

数组长度为：len。

如果len % (len - (next[len] + 1)) == 0 ，则说明 (数组长度-最长相等前后缀的长度) 正好可以被 数组的长度整除，说明有该字符串有重复的子字符串。**数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。**用aab aab aab aab aab最大子串就是aab aab aab aab四个单位。

不难想到：当next[len - 1] != 0 && len % (len - (next[len - 1])) == 0的时候满足题意：可根据下图辅助理解。

class Solution {
    public boolean repeatedSubstringPattern(String s) {
        if (s.equals("")) {
            return false;
        }
        int[] next = new int[s.length()];
        getNext(next, s);
        int len = s.length();
        if (next[len - 1] != 0 && len % (len - (next[len - 1])) == 0) {//当且仅当这时候满足题意.
            return true;
        }
        return false;
    }

    private void getNext(int[] next, String s) {
        int j = 0;//默认next的值是0;
        next[0] = j;//默认next第一位下标是0;
        for (int i = 1; i < s.length(); i++) {//默认next从下标1开始慢慢修改.
            while (j > 0 && s.charAt(j) != s.charAt(i))//只要不匹配,就回退.
                j = next[j - 1];
            if (s.charAt(j) == s.charAt(i))//相等就往后面移动
                j++;
            next[i] = j;//记录当前j的值作为next的值.
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

总结：

KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

什么是KMP，什么是前缀表，以及为什么要用前缀表。

前缀表：起始位置到下标i之前（包括i）的子串中，有多大长度的相同前缀后缀。

那么使用KMP可以解决两类经典问题：

1. 匹配问题：28. 实现 strStr()
2. 重复子串问题：459.重复的子字符串

再一次强调了什么是前缀，什么是后缀，什么又是最长相等前后缀。

前缀：指不包含最后一个字符的所有以第一个字符开头的连续子串。

后缀：指不包含第一个字符的所有以最后一个字符结尾的连续子串。

然后针对前缀表到底要不要减一，这其实是不同KMP实现的方式，本文主要是最原始的前缀表。

其中主要理解j=next[x]这一步最为关键！

参考链接：

帮你把KMP算法学个通透！（理论篇）_哔哩哔哩_bilibili

帮你把KMP算法学个通透！（求next数组代码篇）_哔哩哔哩_bilibili

【宫水三叶】简单题学 KMP 算法 - 实现 strStr() - 力扣（LeetCode）

如何更好地理解和掌握 KMP 算法? - 知乎 (zhihu.com)