OFDM 十六讲 2- OFDM and the DFT - 码农知识堂

OFDM 十六讲 2- OFDM and the DFT

参考：

Iain Explains Signals, Systems, and Digital Comms

前言：

Shows how Orthogonal Frequency Division Multiplexing (OFDM) is implemented with a Discrete Fourier Transform (DFT), and how it relates to single carrier digital communications.

目录

1： 单信道传输模型

2： OFDM 传输模型

3： DFT

一单信道传输模型

单信号传输模型，前面在讲modulation 有讲过。

发送方：

原始的bit流为0,1，经过QPSK等调制，0->1,1->-1

然后经过余弦振荡器调制成高频的模拟信号

加入高斯白噪声，经过信道把数据发出去

接收方

乘以相同频率的余弦信号，就可以解码出t 时刻的bit的 $\hat{x}$

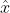
二 OFDM 传输模型

2.1 两路

如上增加了一路正交信号

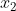
s: 为余弦振荡器，把数字信号调制成模拟信号

$\hat{x_1}=\int_{0}^Tx(t)s_1(t)dt$

$=x_1\int _{0}^{T}s_1^2(t)dt+0$

同理

$\hat{x_2}=x_2\int s_2^2(t)dt$

正交就是一个周期内积分为0

例：

, $f_1=\frac{1}{T}$

$s_1(t)=cos2\pi f_1t$

$s_2(t)=cos2\pi f_2t$

$\int_{0}^T cos 2\pi f_1t* cos2\pi f_2tdt$

$=\frac{1}{2}\int cos2\pi(f_1+f_2)tdt+\frac{1}{2}\int cos2\pi(f_2-f_1)tdt+$

$=\frac{1}{2}\int cos 6\pi f_1tdt+\frac{1}{2}\int cos 2\pi f_1tdt$

$=\frac{1}{2} \frac{sin 6\pi f_1 t}{6\pi}|_{0}^T+\frac{1}{2} \frac{sin 2\pi f_1 t}{6\pi}|_{0}^T$

2.2 多路

实际实现中,不可能有无用大的数。

可以用IDFT（离散傅里叶逆变换表示）Inverse discrete Fourier transform

$x(t)=\sum_{k=0}^{N-1}x_k e^{j(\frac{2\pi}{T}k)t}$

每channel对应的信号频率为 $\frac{k}{T}$ ,跟其它channel的信号正交

另一种形式

傅里叶变换

$F(w)=\int_{-\infty}^{\infty}f(t)e^{-jwt}dt$

傅里叶逆变换

$f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty} F(w)e^{jwt}dw$

傅里叶逆变换原理：

$\int \int f(x)e^{-jwx}dx e^{jwt}dw$

$=\int \begin{bmatrix} \int e^{-jw(x-t)}dw \end{bmatrix}f(x)dx$

$=\int 2\pi \delta (x-t)f(x)dx$

$=2\pi f(t)$

则

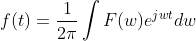
$f(t)=\frac{1}{2\pi}\int F(w)e^{jwt}dw$
相关阅读:
互联网公司研发效能团队为啥必须独立？何时独立？
微信小程序按钮颜色
 智能方案设计——智能跳绳方案
 C进阶-C语言文件操作
 MySQL需要了解的常用命令
 Python使用MySQL，无记录则插入，有记录则更新 - ON DUPLICATE KEY UPDATE
关于离子色谱仪的结构和应用原理分析
 Windows安装cassandra，数小时多个bug总结记录
 代码随想录算法训练营day57 | 647. 回文子串，516.最长回文子序列
 ios16充电卡在80%充不上去了?可以试试这几种办法
原文地址：https://blog.csdn.net/chengxf2/article/details/125989889