-
【对比学习】Understanding the Behaviour of Contrastive Loss (CVPR‘21)
Understanding the Behaviour of Contrastive Loss (CVPR’21)
Contrastive Loss中的温度系数 τ \tau τ 是个关键参数,大部分论文都把 τ \tau τ 设置为一个小数字,这篇文章从分析温度参数 τ \tau τ 出发,分析出:
- 对比损失实际上可以自动挖掘出难负样本,因此可以学习出高质量的自监督表征。具体地,对于已经远离的负样本,不需要让其继续远离;主要聚焦于没有远离的负样本(难负样本),从而使得表示空间更均匀(和下面那个红圈圈图差不多意思)。
- 温度系数 τ \tau τ 可以控制挖掘负样本的程度, τ \tau τ 越小越关注难负样本。
Hardness-Awareness
广泛使用的对比损失函数是InfoNCE:
L ( x i ) = − log [ exp ( s i , i / τ ) ∑ k ≠ i exp ( s i , k / τ ) + exp ( s i , i / τ ) ] \mathcal{L}\left(x_{i}\right)=-\log \left[\frac{\exp \left(s_{i, i} / \tau\right)}{\sum_{k \neq i} \exp \left(s_{i, k} / \tau\right)+\exp \left(s_{i, i} / \tau\right)}\right] L(xi)=−log[∑k=iexp(si,k/τ)+exp(si,i/τ)exp(si,i/τ)]
该损失函数要求第 i 个样本和它另一个扩增的(正)样本之间的相似度 s i , i s_{i,i} si,i 之间尽可能大,而与其它实例(负样本)之间的相似度 s i , k s_{i,k} si,k 之间尽可能小。但是满足这一条件的损失函数很多,比如一个最简单的函数 L simple \mathcal{L}_{\text {simple }} Lsimple :
L simple ( x i ) = − s i , i + λ ∑ i ≠ j s i , j \mathcal{L}_{\text {simple }}\left(x_{i}\right)=-s_{i, i}+\lambda \sum_{i \neq j} s_{i, j} Lsimple (xi)=−si,i+λi=j∑si,j
但这两个损失函数的训练效果差很多:数据集 Contrastive Loss Simple Loss CIFAR-10 79.75 74 CIFAR-100 51.82 49 ImageNet-100 71.53 74.31 SVHN 92.55 94.99 这是因为Simple Loss对所有的负样本相似度给予了相同权重的惩罚: ∂ L simple ∂ s i , k = λ \frac{\partial L_{\text {simple }}}{\partial s_{i, k}}=\lambda ∂si,k∂Lsimple =λ,即损失函数对所有负样本的相似度的梯度是相等的。但是在Contrastive Loss中,会自动给相似度更高的负样本更高的惩罚:
对正样本的梯度 : ∂ L ( x i ) ∂ s i , i = − 1 τ ∑ k ≠ i P i , k 对负样本的梯度 : ∂ L ( x i ) ∂ s i , j = 1 τ P i , j ∝ s i , j \text { 对正样本的梯度 : } \frac{\partial \mathcal{L}\left(x_{i}\right)}{\partial s_{i, i}}=-\frac{1}{\tau} \sum_{k \neq i} P_{i, k} \\ \text { 对负样本的梯度 : } \frac{\partial \mathcal{L}\left(x_{i}\right)}{\partial s_{i, j}}=\frac{1}{\tau} P_{i, j} \propto s_{i, j} 对正样本的梯度 : ∂si,i∂L(xi)=−τ1k=i∑Pi,k 对负样本的梯度 : ∂si,j∂L(xi)=τ1Pi,j∝si,j
其中 P i , j = exp ( s i , j / τ ) ∑ k ≠ i exp ( s i , k / τ ) + exp ( s i , i / τ ) P_{i, j}=\frac{\exp \left(s_{i, j /} \tau\right)}{\sum_{k \neq i} \exp \left(s_{i, k} / \tau\right)+\exp \left(s_{i, i} / \tau\right)} Pi,j=∑k=iexp(si,k/τ)+exp(si,i/τ)exp(si,j/τ),对于所有负样本, P i , j P_{i, j} Pi,j的分母是相同的,所以 s i , j s_{i, j} si,j越大,负样本的梯度项也越大,也就给予了负样本更大远离该样本的梯度。(可以理解为focal loss,越难梯度越大)。从而鼓励所有样本均匀的分布在一个超球面上。为了验证真的Contrastive Loss真的是因为能够挖掘难负样本的特性,文章显示的额外选取一些困难样本用在Simple Loss上(为每个样本选取4096个难负样本),性能大大提升:
数据集 Contrastive Loss Simple Loss + Hard CIFAR-10 79.75 84.84 CIFAR-100 51.82 55.71 ImageNet-100 71.53 74.31 SVHN 92.55 94.99 温度系数 τ \tau τ控制程度
温度系数 τ \tau τ越小,损失函数越关注难负样本,特别地:
当 τ \tau τ趋近于0时,Contrastive Loss退化成只关注最难的样本:
lim τ → 0 + 1 τ max [ s max − s i , i , 0 ] \lim _{\tau \rightarrow 0^{+}} \frac{1}{\tau} \max \left[s_{\max }-s_{i, i}, 0\right] τ→0+limτ1max[smax−si,i,0]
这意味着将挨个把每个负样本推到离自己相同的距离:
当 τ \tau τ趋近于无穷大时,Contrastive Loss几乎退化成Simple Loss,对所有负样本的权重相同。
所以温度系数 τ \tau τ越小,样本特征的分布越均匀,但这也不是好事,因为潜在正样本(False Negative)也被推走了:
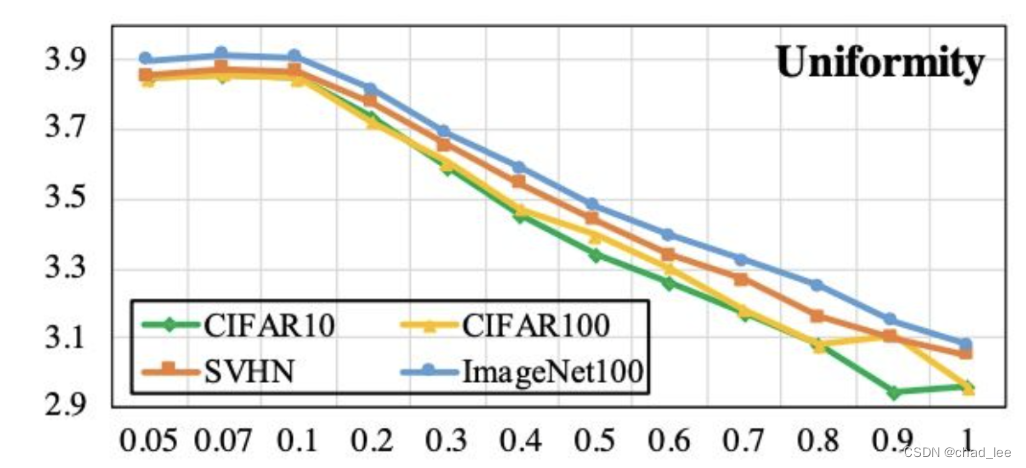
-
相关阅读:
RecyclerView高效使用第二节
【RocketMQ】MMAP零拷贝在RocketMQ中的运用
统计学习方法学习笔记-07-支持向量机03
JAVA-Map接口概述、常用方法、排序、Hashtable面试题
Redisson实现分布式锁案例
vim中粘贴代码片段出现每行新增缩进的解决方法-set paste
场景应用:接口和抽象类有什么区别?你平时怎么用?
vue3解决跨域问题!亲测有效
高效电商数据分析:电商爬虫API与大数据技术的融合应用
C语言——自定义类型之结构体
- 原文地址:https://blog.csdn.net/yanguang1470/article/details/125903355