---

🍌 一.什么是AVL树

在认识AVL树之前我们先认识一下什么是二叉搜索树:

🍓 1.二叉搜索树

二叉搜索树又称为二叉排序树,二叉搜索树满足所有的左孩子节点都小于其根节点的值,所有的右孩子节点都大于其根节点的值,二叉搜索树上的每一棵子树都是一棵二叉搜索树,因此二叉搜索树通过中序遍历可以获得一个有序的序列(由小到大);

类似于这样的树就是一棵二叉搜索树;

🍓 2.为什么引入了AVL树

二叉搜索树看似很美好,但其却有一些缺陷.对于二叉搜索树而言,是和查找相关的，而不论是查找还是删除,都需要先进行查找,也就是对整棵树来进行遍历,而对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度函数,也就是结点越深，则比较次数越多.最优的情况下是：二叉搜索树为完全二叉树，其平均比较次数为：$lo{g}_{2}n$,但是如果二叉搜索树退化成了一棵单分支的树,其平均比较次数为：n/2,就是最差的情况了

这就相当于是一个顺序表的查找了,这样二叉搜索树的优势就完全消失了,因此就引入了AVL树!

🍓 3.什么是AVL树

AVL树又称自平衡二叉查找树,是高度平衡的二叉搜索树,就是在二叉搜索树的基础上进行了优化,既当向二叉搜索树中插入新结点后，保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),也就是降低树的高度,这样就可以减少平均搜索长度了,因此AVL树满足它的左右子树都是AVL树,左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1),这就是AVL树的优势所在,因此如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在 ，搜索时间复杂度O($lo{g}_{2}n$)!!!

平衡因子 = 右子树的高度 - 左子树的高度

---

🍌 二.自己构造AVL树

这里的构造还是和二叉搜索树的构造差不多的，只不过在这里插入元素的话就需要考虑平衡因子的事情了，因为一定要保证插入元素后此树还是一棵AVL树，就需要进行相关调整，这里就先不过多介绍了，下面再详细介绍，先来构造一棵简单的AVL树：

public class AVLTree {
    static class TreeNode{
        //内部类，表示AVL树的每个节点

        //val值
        public int val;
        //左孩子的引用
        public TreeNode left;
        //右孩子的引用
        public TreeNode right;
        //父亲节点的引用
        public TreeNode parent;
        //平衡因子(每个节点都有）
        public int bf;
        public TreeNode(int val){
            this.val = val;
        }
    }

    //根节点
    public TreeNode root;
    public boolean insert(int val){
       
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

这样一棵简单的AVL树就构造好了，下面就来写一下AVL树的插入！

---

🍌 三.AVL树的插入和删除

🍓 1.插入

首先就是将节点插进来，和二叉搜索树一样，先只看位置在哪，不关注平衡因子

这个为要插入节点：

   TreeNode node = new TreeNode(val);
        if(root == null){
            //没有根节点，要插入的就是根节点
            root = node;
            return true;
        }
        //记录每个节点的父节点
        TreeNode parent = null;
        //要移动的代节点
        TreeNode cur = root;
        //根据val的值和root进行比较来确定应该插入节点的位置
        while (cur != null){
            if(cur.val > val){
                //大于证明此节点应在左子树
                parent = cur;
                cur = cur.left;
            }else if(cur.val < val){
                //大于证明此节点应在右子树
                parent = cur;
                cur = cur.right;
            }else {
                //不能有值一样的节点
                return false;
            }
        }
        //此时cur为空，需要找到对应的位置
        if(parent.val > val){
            parent.left = node;
        }else{
            parent.right = node;
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

此时节点就已经插进来了，此时就需要看其每个节点的平衡因子了

        //而此时就需要对树进行平衡因子的调整了，保证树是高度平衡的
        //再反着回去写
        node.parent = parent;
        cur = node;
        //当父亲节点一直存在的时候，就表示没有调到根节点就需要继续调整
        while(parent != null){
            if(cur == parent.right){
                //在右边右树高度加一，因此bf+1
                parent.bf++;
            }else{
                //再左边，左树高度加一，因此bf-1
                parent.bf--;
            }
            //在这里就要进行判断了，如果此时的父亲节点如果平衡因子为0了，那么就不需要再往上走了，因为上面的都是平衡的
	        if(parent.bf == 0){
	            return true;
	        }else if(parent.bf == -1 || parent.bf == 1){
	            //此时父亲节点的平衡因子为1、-1
	             //此时表示当前树平衡了，但是不表示整棵树都平衡了，因此还需要继续往上走
	            cur = parent;
	            parent = cur.parent;
	        }else{
	            //此时父亲节点的平衡因子为2、-2
	            if(parent.bf == 2){
                //此时右树高 需要降低右树的高度
	                if(cur.bf == 1){
	                    //左单旋
	                    rotateLeft(parent);
	                }else{
	                    //右左双旋
	                    rotateRL(parent);
	                }
	            }else{
	                //此时左树高，需要降低左树的高度
	                if(cur.bf == 1){
	                    //左右双旋
	                    rotateLR(parent);
	                }else{
	                    //右单旋
	                    rotateRight(parent);
	                }
	            }
	        }
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

这是当前会出现的问题：

先来讨论一下调整平衡因子会出现的一些情况，来分别看一下：
首先是平衡因子调整为0了，那么就不需要再往上走了，因为上面的都是平衡的，当前的父亲节点的平衡因子为0了表示插入的这个元素只影响到了这一棵树，上面是没有影响的，因此是0的话就结束了

因此是0的话就表示当前已经结束了，不需要再往上了，其他变为0 的情况也是一样的这里就不细画了
而如果是1或者-1的话，表示当前树平衡了，但是不表示整棵树平衡了，因此需要再往上走；
而如果是2或者-2的话，会以下四种情况，再来分别看一下：

🍉 1.1.右单旋

此时左树高，需要降低左树的高度，也就是右旋（parent.bf = -2,cur.bf = -1）：

也就是如下的效果：

也就是这样的调整过程：

下面写一下代码：

private void rotateRight(TreeNode parent){
        //右单旋
        //此时parent的平衡因子为-2，cur的平衡因子为-1
        //需要记录parent的根节点
        TreeNode pParent = parent.parent;

        TreeNode cur = parent.left;
        //记录cur的右节点
        TreeNode curR = cur.right;
        //如果cur有右节点需要赋给parent的左节点，但是没有就不需要给了
        if(curR != null){
            parent.left = curR;
            curR.parent = parent;
        }
        //然后将cur的右孩子改变为parent
        cur.right = parent;
        parent.parent = cur;

        //检查当前是不是根节点，不是根节点需要看是左子树，还是右子树
        if(pParent != null){
            //改变之前的指向
            cur.parent = pParent;
            if(parent == pParent.right){
                pParent.right = cur;
            }else{
                pParent.left = cur;
            }
        }else{
            //此时parent就是root，因为没有根节点
            cur = root;
            root.parent = null;
        }

        //最后记得一定要修改平衡因子
        parent.bf = 0;
        cur.bf = 0;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

这样一个“简单”的右单旋就结束了~

🍉 1.2.左单旋

这种情况就是最开始的情况了
此时右树高，需要降低右树的高度，也就是左旋（parent.bf = 2,cur.bf = 1）：

也就是如下的效果：

也就是这样的调整过程：

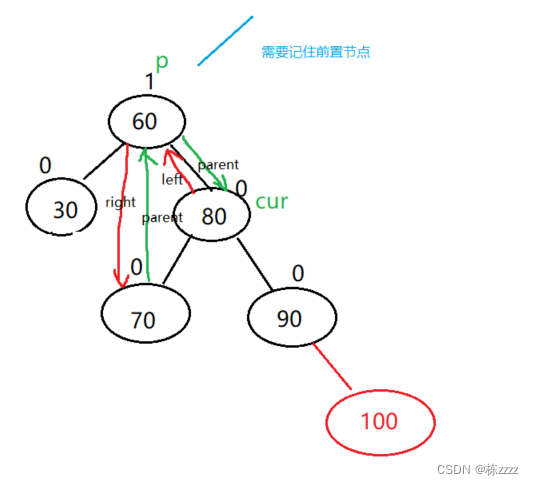
代码如下：

private void rotateLeft(TreeNode parent){
        //左单旋
        //此时parent平衡因子为2，cur的平衡因子为1
        //需要记录父亲节点
        TreeNode pParent = parent.parent;

        TreeNode cur = parent.right;
        //记录cur的左节点
        TreeNode curL = cur.left;
        //判断左节点是不是空的，如果是空的就不需要管了，不是空的就需要将parent右节点指向它，并且它的父亲节点为parent
        if(curL != null){
            //改变指向
            parent.right = curL;
            curL.parent = parent;
        }
        //改变cur的指向
        cur.left = parent;
        parent.parent = cur;
        //判断如果pParent不为空，就表示parent不是root，就需要看其是左孩子还是右孩子
        if(pParent != null){
            cur.parent = pParent;
            if(parent == pParent.right){
                pParent.right = cur;
                
            }else{
                pParent.left = cur;
            }
        }else{
            //是根节点
            cur = root;
            root.parent = null;
        }
        cur.bf = 0;
        parent.bf = 0;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

这样一个“简单”的左单旋就结束了~

🍉 1.3.左右双旋

此时左树高，需要降低左树的高度，（parent.bf = -2,cur.bf = 1）：

而此时仅通过单旋是无法完成的，需要通过两种旋转才能完成：

上面左单旋和右单旋已经介绍过了，这里就不详细介绍了，
先左旋：

此时修改的平衡因子是没有用的
再右旋：

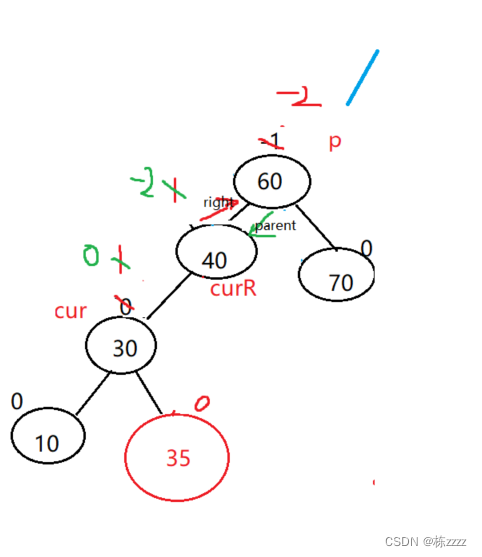
两次旋转之后只需要进行平衡因子的改变就可以了，

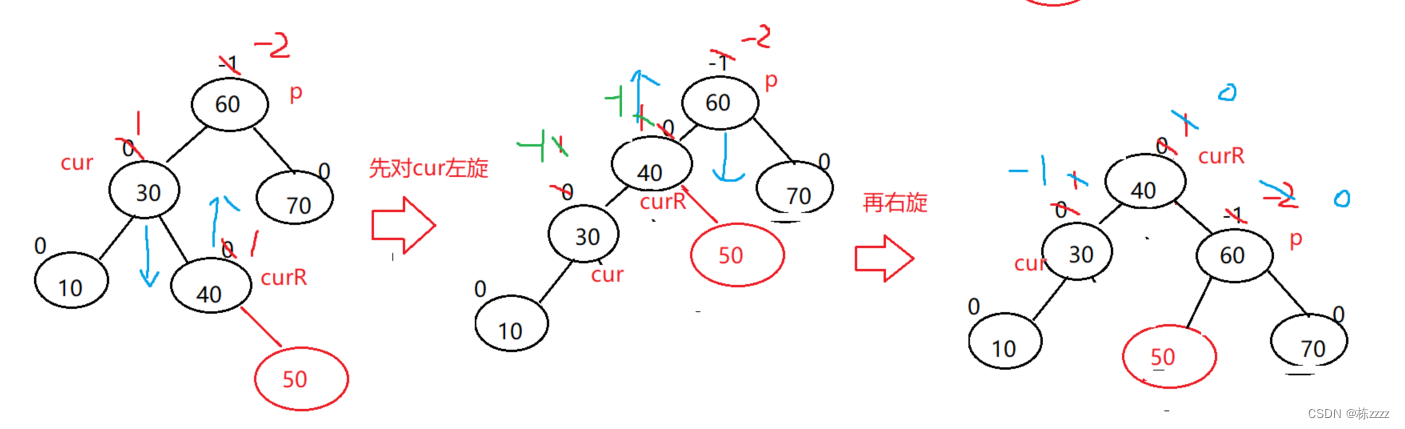
通过观察curR的平衡因子，会决定最后其他节点的平衡因子

代码如下：

private void rotateLR(TreeNode parent){
        //左右双旋
        TreeNode cur = parent.left;
        TreeNode curR = cur.right;
        //此时就需要看curR的平衡因子，再决定最后其他节点的平衡因子
        int bf = curR.bf;
        //先调用左旋再右旋
        rotateLeft(parent.left);
        rotateRight(parent);
        if(bf == -1){
            curR.bf = 0;
            cur.bf = 0;
            parent.bf = 1;
        }else if(bf == 1){
            curR.bf = -1;
            cur.bf = 0;
            parent.bf = 0;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

这样一个左右双旋就结束了~

🍉 1.4.右左双旋

此时右树高，需要降低右树的高度（parent.bf = 2,cur.bf = -1）：

而此时仅通过单旋是无法完成的，需要通过两种旋转才能完成：

先右旋：

再左旋：

通过观察发现其需要改变的平衡因子和curL有关系：

因此
代码如下：

 private void rotateRL(TreeNode parent) {
        //右左双旋
        TreeNode cur = parent.right;
        TreeNode curL = cur.left;
        //此时就需要看curL的平衡因子了，再决定最后其他节点的平衡因子
        int bf = curL.bf;
        rotateRight(cur);
        rotateLeft(parent);

        if(bf == -1){
            cur.bf = 1;
            parent.bf = 0;
            curL.bf = 0;
        }else if(bf == 1){
            parent.bf = -1;
            curL.bf = 0;
            cur.bf = 0;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

🍓 2.删除

删除和上面的插入是差不多的，由于AVL树也是二叉搜索树，可按照二叉搜索树的方式将节点删除，然后再更新平衡因子，只不过与删除不同的是，删除节点后的平衡因子更新，最差情况下一直要调整到根节点的位置。
具体步骤：

1. 找到需要删除的节点
2. 按照搜索树的删除规则删除节点
3. 更新平衡因子，如果出现了不平衡，进行旋转。–单旋，双旋

我这里就不进行完整的代码书写了！！

---

到这儿，AVL树就介绍完毕了，后面会继续介绍红黑树！！！