【c++入门（2）】并查集

并查集(Union Find Set)：是一种用于处理分离集合的抽象数据类型。主要包含2种操作：
查询（Find）：给定一个x，判断x属于哪个集合。
合并（Union）：给定x和y，讲x所在的集合与y所在的集合合并。

实现并查集：

实现方法1：顺序表

在顺序表实现中，使用数组记录每个元素所属的集合代表。A[i] = j，表示元素i所属集合的代表为j
① 初始化：make-set(x)：设置A[x] = x，N个元素的时间复杂度O(N)。
② 查找：find(x)：返回A[x]的值，时间复杂度O(1)。
③ 合并：union(y, x)：如果x和y属于同一个集合，不做任何操作，返回他们所属集合的
代表，否则更新其中一个集合中所有元素的代表为另一个集合的代表，时间复杂度O(N)。

实现方法2：双向链表

在链表实现中，每个分离集合对应一个链表，链表有一个表头(集合代表)，每个元素有一个head指针指向表头，标记其所属集合，一个next指针指向集合中的下一个元素。为了union方便，再添加一个last指针，指向集合中的最后一个元素（只在集合代表中记录last）。
① 初始化：make-set(x)：设置S[x].head = S[x].last = x , S[x].next = 0
② 查找：find(x)：返回S[x].head。
③合并：union(x, y)：如果x和y属于同一个集合，不做任何操作，返回S[x].head，否则将其中一个集合合并到另一个集合，返回合并后集合的代表。

实现方法3：树

在树实现中，每棵树表示一个分离集合，树中的每个节点表示集合的一个成员，每个成员都有一个指向其双亲的指针，用树根作为集合的代表，且根节点的父节点指向其自身。每个分离结合对应的一棵树称为“分离集合树”。
由于每个节点都存储其双亲节点，使用双亲表示法记录“分离集合树”。
双亲表示法：定义数组p[N]，p[i]记录节点i的双亲。
① 初始化：make-set(x)：p[x] = x。
② 查找：find(x)：向上查找x的双亲，直到根节点，返回根节点的编号。
③ 合并：union(y,x)：如果x和y属于同一个集合，不做任何操作，返回x所在分离集合树的根，否则将其中一棵分离集合树的根节点的双亲指向另一棵分离集合树的根节点。
考虑时间复杂度：
h表示x所在的“分离集合树”的深度。
初始化：复杂度O(N)
查找：要遍历x所在的“分离集合树”，直到找到根，时间复杂度为O(h)
查找x,y所在集合代表复杂度O(h)，单修改复杂度：O(1)，总复杂度O(h)

树的性能优化：

优化思想：降低“分离集合树”的深度。
优化·：按秩(rank)合并：在执行union操作时，优先将深度低的树合并到深度高的树中。
优化2：路径压缩：在执行find(x)操作时，将x及其祖先的双亲都更新为根节点，降低树的深度。
例如：下图所示的分离集合树在调用find(5)后会转变为右侧的B树，深度从5降为了3。

连通分量

概念1：连通图

连通图：如果无向图G中，任意两个顶点vi和vj都是连通的，则称G是连通图。
拥有n个顶点的连通图，至少有n - 1条边。

概念2：连通网

连通网：带权值的连通图称为连通网。

连通图：

非连通图：
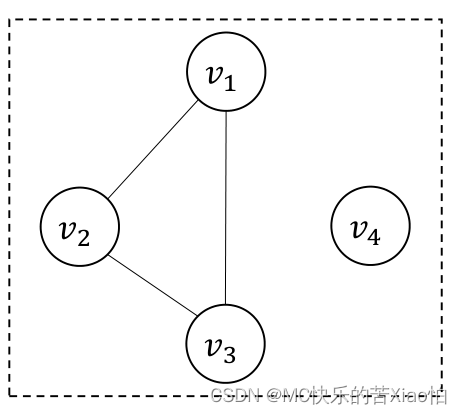连通网：

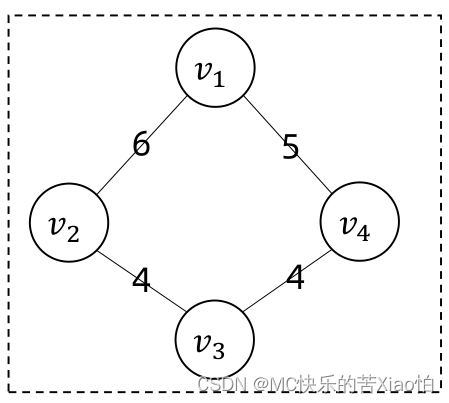
概念3：连通分量

连通分量：无向图中的极大连通子图称为连通分量，连通分量包含以下特征：
① 要是子图。
② 子图要是连通的。
③ 该连通子图含有极大顶点数。
④ 具有极大顶点数的连通子图包含依附于这些顶点的所有边。

并查集求连通分量：

并查集求连通分量时，无需预先存边，节省空间，时间复杂度也很低，对于每条边 (u, v) 进行一次union(u, v)操作，合并完成后，每个“分离集合”即是一个连通分量。

例题：

    Farmer John and Betsy are playing a game with N (1 <= N <= 30,000)identical cubes labeled 1 through N. They start with N stacks, each containing a single cube. Farmer John asks Betsy to perform P (1<= P <= 100,000) operation. There are two types of operations:
    moves and counts.
    * In a move operation, Farmer John asks Bessie to move the stack containing cube X on top of the stack containing cube Y.
    * In a count operation, Farmer John asks Bessie to count the number of cubes on the stack with cube X that are under the cube X and report that value.

    Write a program that can verify the results of the game.

    有n个箱子，初始时每个箱子单独为一列；
    接下来有p行输入，M, x, y 或者 C, x；
    对于M,x,y：表示将x箱子所在的一列箱子搬到y所在的一列箱子上；
    对于C,x：表示求箱子x下面有多少个箱子； 
Input
    * Line 1: A single integer, P

    * Lines 2..P+1: Each of these lines describes a legal operation. Line 2 describes the first operation, etc. Each line begins with a 'M' for a move operation or a 'C' for a count operation. For move operations, the line also contains two integers: X and Y.For count operations, the line also contains a single integer: X.

    Note that the value for N does not appear in the input file. No move operation will request a move a stack onto itself.

    第一行一个整数P,表示操作次数。
    接下来有p（1<= P <= 100,000）行输入，M, x, y 或者 C, x；（x,y<=N）
    箱子的个数N，不会出现在输入中。（1 <= N <= 30,000），初始时每个箱子单独为一列；你可以认为，操作过程中，不会出现编号大意30000的箱子 
Output
    Print the output from each of the count operations in the same order as the input file.
    对于每个询问，输出相应的值。
Sample Input

    6
    M 1 6
    C 1
    M 2 4
    M 2 6
    C 3
    C 4

Sample Output

    1
    0
    2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

思路1：链表
很重要的复杂度堆在了合并上面，使用链表可以使用O(1)复杂度解决操作1：
将x集合最底下的箱子的后继设为y集合最上面的箱子，完成合并x,y操作。
但是操作2：
操作2是知道x下面有多少个箱子，使用链表必须一个一个遍历，直到没有后继，复杂度：O(n)
并且想要这样遍历显然需要双向链表实现，写起来很麻烦，并且还有很多不确定的因素，所以先不考虑用链表实现。
思路2：并查集

想一想为什么链表实现不了，是因为操作2的时候我们只能一个一个遍历。其实，我们每次遍历找到根后就可以直接将x的后继设为根，可以直接找到根：
这样可以快速找到根，写成一个函数：

int getfa (int x)
{
    if (fa[x] == x) return x ;
    return fa[x] = getfa (fa[x]) ;
}
1
2
3
4
5

合并x , y 就是：

fa[getfa (x)] = getfa (b) ;
1

假设数组dis[i]表示i下面的箱子数，sz[i]表示集合的元素个数。
其实是不是我们可以不用把每一个dis和sz都赋成答案，把答案记录在集合i的根就可以了，因为集合的每个元素都可以通过getfa找到根。
将集合x -> y：

sz[y] += sz[x] ;
1

答案更新：

dis[x] += sz[b] ;
1

所以这题就可以很快的解决了：

#include <bits/stdc++.h>

using namespace std ;

const int N = 30010 ;
int fa[N] , dis[N] , sz[N] ;
//fa记录每一个箱子的father前驱，dis表示每个箱子下面的箱子个数，sz记录每一个集合的箱子个数 
int n = 30000 , m ;
int x , y , t ;
char op ;
int getfa (int last)
{
	if (fa[last] == last) return last ;  //找到 
	int t = getfa (fa[last]) ;  //t = last的前驱的前驱 
	dis[last] += dis[fa[last]] ; 
	//因为是往下查找，所以它的前驱一定是在它的下面，所以应该把它算进last下面的个数 
	fa[x] = t ;   //重要的一步：直接连接first 和 end
	return fa[x] ;  //往下继续寻找根 
}

int main ()
{


	while (cin >> m)
	{
		for (int i = 1; i <= n; i++) fa[i] = i , dis[i] = 0 , sz[i] = 1 ; //初始化 
		while (m -- )
		{
			cin >> op ;
			if (op == 'M')
			{
				cin >> x >> y ;
				int xx = getfa (x) , yy = getfa (y) ;   //找到x和y所在的集合
				fa[xx] = yy ;   //合并操作：连接两个集合
				dis[xx] += sz[yy] ;  //底下多了y集合那么多箱子
				sz[yy] += sz[xx] ;  //x和y合并成一个集合，该集合的元素个数是x + y 
			}
			else
			{
				cin >> x ;
				getfa (x) ;  //通过根找到答案 
				cout << dis[x] << endl ;
			}
		}
	}


	return 0 ;
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

练习：
连通 OR 不连通：

题目描述

给定一个无向图，一共n个点，请编写一个程序实现两种操作：

D x y 从原图中删除连接x，y节点的边。

Q x y 询问x，y节点是否连通
输入格式

第一行两个数n,m（5<=n<=100000,1<=m<=100000）

接下来m行，每行一对整数 x y （x,y<=n）,表示x,y之间有边相连。保证没有重复的边。

接下来一行一个整数 q（q<=100000）

以下q行每行一种操作，保证不会有非法删除。
输出格式

按询问次序输出所有Q操作的回答，连通的回答C，不连通的回答D。
输入输出样列
输入样例1：

3 3
1 2
1 3
2 3
5
Q 1 2
D 1 2
Q 1 2
D 3 2
Q 1 2

输出样例1：

C
C
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

思路：
该问题要求一遍删边，一遍判断顶点x, y是否属于同一个连通分量。
DFS求连通分量，时间复杂度：O(N + M) 每次查询前都需要重新求解连通分量，总时间复杂度：O((N + M) * Q)
并查集删边时，需要将基于这条边所合并的集合分离，并查集并不支持分离操作。
初始时，只处理不会被删的边。接着逆向处理q次操作，如果是Q操作，直接判断x和y是否属于同一个集合，如果是D操作，则union(x, y)，缓存判断结果，最后逆向输出。

拜拜！