矩阵分析与应用-06-概率密度函数01

矩阵分析与应用-06-概率密度函数01

概率密度函数

实随机向量的概率密度函数

一个含有m 个随机变量的实值向量

$x(\xi)=[x_1(\xi),x_2(\xi),...,x_m(\xi)]^T$

称为mx1实随机向量，或简称随机向量(当维数无关紧要时)。其中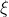， $\xi$ 表示样本点，可以是时间，频率，或者位置等。

一个随机向量由它的联合累积分布函数或联合概率密度函数完全描述。一组概率的集合函数

$F(x) = P\left \{ \xi:x_1< x_1(\xi)\leq x_1,...,x_m< x_m(\xi)\leq x_m \right \}$

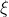定义为向量x( $\xi$ )的联合累积分布函数，简称分布函数。式中，为实数。

随机向量x( 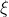$\xi$ )的（联合)概率密度函数定义为

$f(x)=\lim_{\Delta x_1\rightarrow 0,...,\Delta x_m\rightarrow 0}\frac{P\left \{ \xi:x_1< x_1(\xi)\leq x_1+\Delta x_1,...,x_m< x_m(\xi)\leq x_m+\Delta x_m \right \}}{\Delta x_1,...,\Delta x_m} = \frac{\vartheta ^m}{\vartheta x_1...\vartheta x_m}F_x(x_1,...,x_m)$

联合概率密度函数的m-1重积分函数

$F(x_i)=\int_{-\infty }^{\infty} ...\int_{-\infty }^{\infty}f_\infty(x_1,...,x_m)dx_1...dx_m$

称为随机变量的边缘概率密度函数。

就是说，随机向量x( 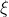$\xi$ )的联合分布函数等于其联合概率密度函数的积分。

随机变量 $x_1(\xi),x_2(\xi,..,x_m(\xi))$ 称为(联合)独立，若对于m个事件 $\left \{ x_1(\xi \leq x_1) \right \},...,\left \{ x_m(\xi \leq x_m) \right \}$ ，有以下概率关系成立：

$P\left \{ x_1(\xi)\leq x_1,...,x_m(\xi)\leq x_m \right \} = P\left \{ x_1(\xi)\leq x_1 \right \} ...P\left \{ x_m(\xi)\leq x_m \right \}$ 。

复随机向量的概率密度函数

一个复随机变量定义为 $x(\xi)=x_R(\xi)+jx_1(\xi)$ ，其中， $x_R(\xi)$ 和 $x_I(\xi)$ 分别为实值随机变量。

复随机向量可以表示成

$x(\xi) = x_R(\xi) + jx_1(\xi)=\begin{bmatrix} x_{R1}(\xi)\\ x_{R2}\xi)\\ ...\\ x_{Rm}(\xi) \end{bmatrix} + j\begin{bmatrix} x_{I1}(\xi)\\ x_{I2}\xi)\\ ...\\ x_{Im}(\xi) \end{bmatrix}$

复随机向量的累计分布函数定义为

$F(x)=P\left \{x(\xi) \leq x \right \}=P\left \{ x_R(\xi) \leq x_R,x_I(\xi) \leq x_R \right \}$

概率密度函数

$f(x) = \frac{\vartheta ^{2m}F(x)}{\vartheta x_{R1}\vartheta x_{I1}...\vartheta x_{Rm}\vartheta x_{Im}}$

累积分布函数是概率密度函数关于所有实部和虚部的2m重积分，即

$F(x)=F_x(x_1,..,x_m)=\int_{-\infty}^{x_{R1}}\int_{-\infty}^{x_{I1}}...\int_{-\infty}^{x_{Rm}}\int_{-\infty}^{x_{Im}}f(v_1,...,v_m)dv_{R1}dv_{I1}...dv_{Rm}dv_{Im}$

特别：

$\int^{\infty}_{-\infty}f(x)dx = 1$
相关阅读:
leetcode：2454. 下一个更大元素 IV【sortedDict初探 + 双单调栈学习】
【产品经理】微信面试题：微信是将天平倾向于信息发送者还是信息接受者？
【校招VIP】测试计划之loadrunner分析
 努力打卡每天学习不浪费每一天 Day43
python项目调优合集（长期更新）：梯度爆炸、消失
 玩转gRPC—深入概念与原理
 新型智慧公厕建设：引领公厕行业的未来！
虚拟机中Linux下安装服务器
 13届蓝桥杯省赛PythonB组真题-蜂巢
 120.(前端)商品管理增加基本信息优化——控制tabs切换下一级目录
原文地址：https://blog.csdn.net/Xiao__fly/article/details/125608873

概率密度函数

实随机向量的概率密度函数

复随机向量的概率密度函数