应用统计学考研笔记：数据整理与抽样案例

题：数据组（4，7，8，6，6，4，5，5，3，6)的众数为（6）

• 解：最多的数据为6，有3个。

题：下列计量属于集中趋势的是(C)。A. 总体单位数 B. 样本单位数C．平均数 D. 方差

• 解：B，算数平均数

题：在下列数据集的综合度量指标中，最容易受到极端值影响的是 （A）。 A、极差 B、上四分数 C、中位数 D、众数

• 解：极差为最大值和最小值的差，因此容易受到极值影响。

题：计算一组数据的标准差时，如果每一个数值加上一个常数a，与原数据组标准差相比，新数据组的标准差(C)。 A．大   B．小   C．不变  D．不一定

• 解：C，样本标准差的计算公式，若令每一数值加上一个常数a后的数值为xi′，则xi′＝x＋a，那么每一数值加上一个常数后的样本均值x＿′＝x＿＋a，所以根据公式可知，新数据组的样本方差S2的大小不变，则新数据组的标准差S也不变。

题：数据28，25，26，25，30，27的中位数是（B） A．26 B．26.5 C．27 D．27.5

• 解：排序：25，25，26，27，28，30，中位数在26和27之前，26+27/2=26.5

题：数据88，85，89，87的极差是（D）。 A．1 B．2 C．3 D．4

• 解：极差为最大值减去最小值，即89-85=4

题：下列数据集中的综合度量指票标中，最不容易受极端值影响的是（C）。 A．均值 B．上四分位数 C．中位数 D．众数

• 解：极端值的变化对于数据顺序中的中位数毫无影响。其他多少都会有一定影响。

题：当计算一个时期到另一个时期的销售额的年平均增长速度时，应采用（D）A．众数 B．中位数 C．算术平均数 D．几何平均数

• 解：计算增长速度、比率还有等比数列的平均数时，适宜使用几何平均数，调和平均数只是简单平均数的另一种表示形式，不适于计算平均增长速度，中位数适合顺序数据，众数适合分类数据。

题：对于某股票30天内的每日收盘价数据组成的数据集，简要说明其标准差大小的实际意义。

• 解：标准差是统计中常用的度量数据离散程度的指标，它用数据自身与平均数之差的大小加权，因而区别对待了大小不同的数据，距离平均数远的数据权重比较大，距离平均数近的数据权重比较小，比较合理地反映了不同数据对离散度量的作用。股票30天内的每日收盘价数据集的标准差大小反映了每日收盘价的离散程度。标准差越大，离散程度越大;标准差越小，离散程度越小。

题：有人说：“当数据偏态程度较大时，应选择众数或者中位数等代表集中趋势，而不应使用均值。”这话对吗？为什么？

• 解：正确，当数据偏态程度较大时，说明数据中存在极端值。而均值的一个主要缺点是它对极端值特别敏感（极端值就是数据集中特别大或特别小的个别数据）。但是中位数和众数对极端值不像平均数那么敏感，受极端值的影响较小，具有统计上的稳健性，所以当数据偏态程度较大时，应选择众数或者中位数等代表集中趋势。

题：在连续的变量中，如果分布没有明显的最高点或者数据个数不多，则众数不存在。这种判断正确吗？为什么？

• 解：不正确，具体分析如下：

  （1）众数是指数据中出现次数最多的变量值。对于一组数据，众数可以不止一个。

  （2）众数的主要缺点是一个数据集可能没有众数，或众数不**，而数据集的平均数和中数都是存在并且**的。它的优点是它反映了数据集中最常见的数值，即最普遍的数值，并且它不仅对数量型数据集有意义，对分类型数据集也有意义。

题：某人每天乘公共汽车上班，随机选取10天，记录所花费的时间如下（分钟）：
 28 29 32 37 33 25 29 32 41 34

（运算过程保留小数点后一位。）
（1）对上述数据做茎叶图（以十位数为茎，个位数为叶）。

排序：25 28 29 29 32 32 33 34 37 41

图：

2|5899|4

3|22347|5

4|1|1
（2）估计每天乘公共汽车上班所花费的平均时间。

• 解 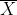：=(25+28+29 +29+32+32+33+34+37+41)/10 

        = 320/10=32

（3）计算乘公共汽车上班所花费时间的样本标准差。

•         方差公式：
•  =( +++++++++)/10-1

        = (+++++++++）/9

        =(49+16+9+9+0+0+1+4+25+81)/9

        = 194/9 = 21.56

• 样本标准差S =         = 4.6

（4）该人也可以乘另一线路公共汽车上班，根据随机选取的10天，计算乘该线路汽车上班所花费的样本平均时间为28分钟，样本标准差为5.8分钟。从时间角度看，哪一条线路比较好？请说明理由。

• 解：

题:某高校18个本科毕业毕业后的起薪为（单位：元）
26496, 35448, 23318, 28905, 23447, 28226,
28040, 26686, 35084, 29530, 31212, 23659,
31817, 22179, 32166, 29730, 30865, 18955
（1）以15000为起点，取区间长度为5000元，将上述数据用频数分布表表示：（1分）
（2）按（1）的结果画频率或频数直方图：（1分）
（3）计算他们的平均年薪（2分）
（4）计算他们的年薪中位数（2分）
（5）计算年薪的极差（2分）

• 解：

  (1)以15000为起点，取区间长度为5000元，定各组界限值，确定分点。各组区间依次为：

  　数出各组频数， 计算频率，作出频数分布表：

        (3)平均年薪= (26496+23318+23447+28040+35084+31212+31817+32166+30865+35448+28905+28226+26686+29530+23659+22179+29730+18955)/18=505763/18=28098(元)

　　(4)将数据从小到大排列，第九个和第十个数据的平均值为年薪的中位数，

　　中位数=(28226+28905)/2=28565.5

　　(5)年薪的极差=35448-18955=16493(元)。